SEO-Константа
Яндекс.Директ + оптимизация
В свое время алгоритм Google PageRank [13] был очень эффективным методом ранжирования интернет-страниц в органическом поиске, и именно он лег в основу сортирующих алгоритмов практически всех без исключения поисковых машин (например, его прямым аналогом на Яндексе является вИЦ, а в случае его подсчета по хостам / директориям (рассмотрено нами в HostRank / DirRank) с соответствующим учетом их тематической составляющей — тИЦ), однако с течением времени, результаты стали искажаться за счет активного вмешательства SEO-компаний и частных лиц, занимающихся продвижением коммерческих сайтов. Сообщается [12], что около 70% всех интернет-страниц в доменной зоне .BIZ и порядка 35% документов в .US относится спамденсингу. Причина, по которой объемы спама только увеличиваются, заключается в том, что все большее количество веб-мастеров желают оказаться в ТОП10 и получать большее количество трафика по интересующих им запросам и, соответственно, больший доход. Для увеличения рейтинга HTML-страниц SEO-оптимизаторы используют ключевые слова как в содержимом самого документа, так и в его основных мета-секциях; увеличивают цитируемость документов в Сети за счет проставления/покупки ссылок [7, 12], но все эти действия расцениваются поисковыми машинами как вмешательство в их алгоритмы, ухудшающие качество поисковой выдачи.
Сейчас, для борьбы с контентным спамом в основном используется машинное обучение, пример которого мы рассматривали в предыдущей части нашего с вами материала, где оценивали результаты классификации сплогов посредством SVM. Говоря простым языком, для эффективного машинного обучения мы предварительно извлекаем из цифрового документа особенности его текстового содержимого, отмечаем некоторое множество страниц в качестве спама или Не-спама, а затем применяем технологию контролируемого обучения (иногда ее также называют, обучением с учителем, где в качестве учителя выступает сама выборка) для пометки всех прочих документов в Сети [5, 12]. За все время наших публикаций по теме спамденсинга, мы уже рассмотрели восемь алгоритмов, использующих в своей работе ссылочную информацию, таких как Google TrustRank, HostRank / DirRank, Truncated PageRank, Google BadRank / ParentPenalty, SpamRank и, наконец, Anti-TrustRank. Здесь, особенно важное значение приобретает то обстоятельство, что, во-первых, в их основу положена парадигма Google PageRank, а во вторых, тот же самый Яндекс может применять схожие анти-спам технологии в своей борьбе с некачественными документами, поэтому их изучение с нашей точки зрения является важным аспектом качественного продвижения и оптимизации сайтов под любую поисковую машину. Сегодня авторитетность той или иной странички в интернете может определяться либо ее текстовым содержимым, либо гиперссылочной структурой, либо поведением пользователей, либо, наконец, комбинацией всех трех факторов (это самый вероятный сценарий), но первоочередной задачей настоящих публикаций является фокусировка именно на методах ссылочного ранжирования.
Для понимания логики, положенной в основу следующего замечательного алгоритма, который называется DiffusionRank, нам потребуется предварительное обращение к модели тепловой диффузии. Однако прежде этого, давайте вкратце пройдемся по тем ранжирующим методам и физическим процессам, что напрямую связаны с изложенной работой. Введем для себя ряд необходимых обозначений. Укажем статический граф G = (V,E), где V = {v1, v2,…, vn), E = {(vi,vj)| есть ребро из vi в vj. Полустепень захода и исхода страницы i обозначим за Ii и di соответственно. Для Google PageRank: мы не можем оценивать документы на основании субъективных читательских предпочтений, уровня их знаний и персонального отношения [13], но усредненное значение читательского круга уже может выступать в качестве объективного показателя, и модель Google PageRank пытается найти его посредством учета глобальной ссылочной структуры, содержащей огромное количество статистических данных. В случае алгоритма PageRank веб представляется в виде ориентированного графа G, а голосующая способность xi страницы vi∈V рекурсивно определяется голосующей способностью документов, ссылающихся на нее: xi=∑(j,i)∈Eaijxj, где предполагается, что aij=1/dj, если имеется ссылка из j в i; в противном случае 0. Или в матричном выражении x = Ax. С учетом концепции «случайного прыжка», имеем:
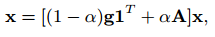
где α является вероятностью прохождения по ссылке, (1 — α) вероятностью совершения «случайного прыжка», а g — стохастическим вектором телепортации, то есть 1Tg = 1. Стандартно, α = 0.85, а g = 1/n1, где 1 — это вектор из одних единиц [6, 13]. Для TrustRank: алгоритм доверия [7] можно поделить на две части. В первой, которая заключается в отборе документов для трастовой выборки, предполагается применение обратного PageRank. Жестко связанная с классическим алгоритмом, эта инверсивная модель помогает экспертам более эффективно определять подходящие для нас интернет-узлы. Во второй части используется Biased PageRank, в котором стохастическое распределение g учитывает все качественные и трастовые страницы, отобранные на первом этапе. В наших прошлых публикациях на тему детекции поискового спама мы уже подробно описывали вам алгоритм Trust Rank, поэтому сейчас акцентироваться на деталях его работы мы не будем.
Для Manifold Ranking: в [17] предлагается идея алгоритма ранжирования данных, с учетом их внутренних связей. Данные, представленные в виде векторов в Евклидовом пространстве, рассматриваются как извлеченные из многообразия. По ним мы создаем неориентированный взвешенный граф, вершинами которого выступают сами данные, а дуги задаются евклидовым расстоянием между ними (вычисляется как Евклидова мера или скалярное произведение векторов); матрица весов подвергается сглаживанию Гауссовским ядром. Несмотря на то, что алгоритм ранжирования связанных структур позволяет достичь впечатляющих результатов в сортировке изображений (кроме текстовой и графической, он также может ранжировать и мультимедийную информацию), нам неизвестны вектор g и K-параметр персонализированного PageRank из [17], а потому мы не можем включить его в последующее сравнение с нашей методологией. Однако отметим, что в машинном обучении многообразие используется достаточно широко, в том числе для уменьшения размерности (обычно, данные являются некоторым подмножеством векторного пространства с ощутимой размерностью, однако их латентная размерность значительно меньше) и классификации. Для термодиффузии: в общем виде, она заключается в том, что при наличии постоянной разницы (градиента) температур по обоим сторонам перегородки, разделяющий одно и то же вещество, возникает, увеличивается и становится константой разница давлений, даже в том случае, если первоначально ее не существовало. Здесь нас в основном будет интересовать теплопроводность, то есть передача тепла от более нагретой точки к той, которая имеет меньшую температуру. Для описания количество тепла, полученного из одной точки в другую, используется ядро теплопроводимости. Для себя отметим, что поскольку для точки с единичной массой температура и тепло будут эквивалентны, то в настоящем материале оба эти термина являются взаимозаменяемыми.
Экстраполяция модели тепловой диффузии позволяет нам взглянуть как на уже привычную для нас модель интернет-графа, так и на методологию расчета важности веб-страниц с совершенно иного ракурса. В текущем материале цифровые документы рассматриваются нами как извлеченные из многообразия, ориентированный ссылочный граф представлен в качестве аппроксимации многообразия, а соответствующие взаимоотношения между страницами отображает ядро теплопроводимости. Равномерное распределение температуры, заданное изначально, по прошествии некоторого интервала времени (то есть после эффекта диффузии) будет являться для нас оценкой значимости веб-документов, которая будет более объективной, в отличие от тех, что присуждаются алгоритмами PageRank и TrustRank.
Существует две причины, объясняющие сегодняшнюю восприимчивость классического Google PageRank к поисковому спаму:
Вышеобозначенное свойство независимости Google PageRank можно объяснить следующим образом: P = [(1 — α)g1T + αA] является положительной стохастической матрицей, если g будет положительным стохастическим вектором телепортации (одним из установочных параметров является равномерное распределение). Тогда, Теорема Перрона [11] гарантирует нам, что наибольшее собственное значение положительной матрицы равно 1 и оно строго больше любого другого собственного значения матрицы, и ему отвечает положительный собственный вектор. Допустим собственный вектор равен 1, тогда мы имеем Py = y. Пусть {xk} будет последовательностью, создаваемой итерационной вычислительной схемой xk+1 = Pxk, а начальный вектор x0 — входным значением. Если {xk} сходятся к x, тогда k+1 = Pxk означает, что x должен удовлетворять Px = x. Поскольку максимальным собственным значением матрицы является только 1, мы имеем x = cy, где c — константа, и в том случае, если вектора x и y нормализированы, тогда c=1. Таким образом, Google PageRank не зависит от входного значения x0, что и требовалось доказать.
По нашему мнению, вектор телепортации g и α объективные параметры, первый из которых определяется пользовательским поведением [1] (как правило, g=1/n1), а значение второго (α=0.85) — результат консенсуса. В отличие от A, α и стохастического вектора g, алгоритм Trust Rank не соответствует «истинной» веб-структуре за счет необъективности g, хотя и представляется эффективным в борьбе с поисковым спамом [7]. Мы же хотим предложить такой алгоритм ранжирования, который не только станет превосходным инструментом в борьбе со спамденсингом, но и как PageRank будет учитывать реальную структуру интернета. Нами было обнаружено, что модель тепловой диффузии является естественным способом устранения излишней демократичности (кроме всего прочего, наличие на сайте большого числа «голосующих по праву своего создания» страниц увеличивает и вероятность выхода на него пользователей, поэтому продвижение сайтов, как правило, активно использует данную методику) и независимости Google PR от входных значений. Поскольку передача тепла всегда следует от позиции, имеющей более высокую температуру к тем, чья температура ниже, то точки размещаются неравномерно по причине появления некоторых из них с высокими температурами, а других с низкими. С другой стороны, различное изначальное распределение температуры будет приводить к различному распределению температуры по истечению некоторого периода времени. Отметим, что воздействие различных геометрических величин на всевозможные поведененческие модели термодиффузии будет взаимным. Говоря о передаче тепла в многообразии на заданном отрезке времени, можно утверждать, что в случае наличия двух точек x и y, оно происходит тогда, когда точка x (с меньшей температурой) получает некоторое количество тепла от y (с большей температурой); тогда мы говорим, что x и y изоморфны, что следует из их сильной взаимосвязанности. Сейчас мы вкратце опишем вам использование эффекта термической диффузии на многообразии, что рассматривается нами только как идеальный вариант, напрямую неприменимый на реальных условиях Глобальной Сети. Тепловой поток, проходящий сквозь геометрическое многообразие с начальными условиями может быть описан с помощью следующего дифференциального уравнения второго порядка: ∂f(x,t)/∂t — Δf(x,t)=0, где f(x,t) — тепло в точке x в момент времени t, а Δf – инвариантный оператор Лапласа–Бельтрами второго порядка, действующий на f. Ядро теплопроводимости Kt(x,y) является здесь специальным решением уравнения теплопроводимости в заданной области с особыми начальными условиями: Kt(x,y) будет описывать нам распределение тепла во времени t, рассеиваемое из его начального источника в точке y (при этом мы подразумеваем, что в других точках тепла нет) и, таким образом, описывать нам связанность (под котором мы подразумеваем изоморфность) между точками x и y. Как уже говорилось – это чисто теоретическая модель, и для того, чтобы перейти к ее практической реализации, сперва нам потребуется рассмотреть теплопроводность на неориентированном и ориентированном графе, а затем воссоздать ее и на случайном графе.
На неориентированном графе G, ребро (vi,vj) рассматривается нами в качестве канала, соединяющего узлы vi и vj. Значение fi(t) описывает температуру в узле vi на момент времени t, следующую из начального распределения температуры fi(0) в нулевой момент времени. Соответственно, вектор fi(t)(fi(0)) включает в себя fi(t)(fi(0)). Саму модель мы строим следующим образом: пусть в момент времени t всякий узел i получает M(i,j,t,Δt) некоторое количества тепла от соседнего узла j на протяжении временного интервала Δt. Получаемое тепло M(i,j,t, Δt) пропорционально временному периоду Δt и температурной разнице fj(t) — fi(t), а потоки тепла из узла j к узлу i проходят по соединяющему их каналу. На основании этого, мы можем предположить, что M(i,j,t,Δt)=γ(fj(t) — fi(t))Δt. В результате, температурная разница в узле i между временем t + Δt и t будет соответствовать сумме тепла, полученного от всех узлов из его окружения. Если говорить более формально, то:
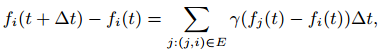
,где E является набором ребер. Для нахождения конечного вида данного уравнения давайте выразим его в матричной форме: (f(t + Δt) — f(t))/Δt = γHf(t), где d(v) обозначает степень узла v. В пределе Δt → 0 имеем d/dt f(t)=γHf(t). Решая его, получаем f (t) = eγtHf(0), в том числе:
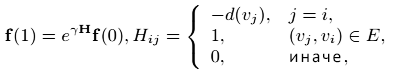
,где eγH определяется как eyH = I + γH + γ2/2! H2 + γ3/3! H3 +… Модифицируем наш граф, добавив его ребрам направления так, чтобы у нас получился ориентированный граф. Дело в том, что когда веб-мастер создает на своей странице ссылку (a,b) на некоторый документ b, он направляет на цитируемый им ресурс энергетический поток (например, пользовательский трафик), который, в приведенном примере будет односторонним, то есть от страницы a к b. На нашей модели это отразится следующим образом: на ориентированном графе G энергетический поток направлен по каналу (vi,vj) таким образом, что тепло поступает только с узла vi к vj, но не наоборот. Пускай в момент времени t каждый узел vi получает RH = RH(i,j,t,Δt) количества тепла из узла vj на протяжении периода Δt. Сделаем ряд допущений: 1) RH должно быть пропорционально периоду времени Δt; 2) RH должно быть пропорционально температуре в узле vj; 3) В том случае, если ссылки между vj и vi не существует, значение RH равно нулю. В результате, vi получает ∑j:(uj,ui)∈Eσjfj(t)Δt количества тепла со всего своего ссылочного окружения. С другой стороны, и узел vi будет диффундировать DH(i,t,Δt) количества тепла своим последователям. Мы полагаем, что: 1) Тепло DH(i,t,Δt) должно быть пропорционально периоду времени Δt; 2) DH(i,t,Δt) должно быть пропорционально температуре в узле vi; 3) Каждый узел обладает способностью распространять тепло; 4) Ко всем последователям тепло DH(i,t,Δt) распределяется равномерно. Конечно, реальная картина представляется куда более сложной, чем та, которую мы вам сейчас обрисовали, но для нашей упрощенной модели этого будет вполне достаточно. Как результат, узел vi будет диффундировать γfi(t)Δt/di количества тепла своим последователям, каждый из которых будет получать γfi(t)Δt/di тепла. Отсюда, σj=γ/dj. В конечном счете, температурная разница в узле vi в промежутке времени t+Δt и t будет соответствовать сумме полученного тепла от всех предшественников, за вычетом того объема, которое он диффундирует своим последователям. Формально это можно записать следующим образом: fi(t+Δt)-fi(t)= -γfi(t)Δ+∑j:(uj,ui)∈Eγ/djfj(t)Δt. Кроме того, мы получаем:
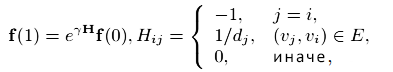
Для того, чтобы сделать нашу модель более гибкой давайте посмотрим на наш граф с позиции вероятности, сделав все его ориентированные ребра случайными, то есть мы будем выпускать ребро из узла vi к узлу vj с вероятностью (1-α)gj. Интересно, что с помощью случайных графов и моделей копирования мы можем дать очень оригинальное объяснение степенному закону распределения полустепени захода и Google PageRank, который действует как в Глобальной Сети, так и в нашей с вами реальной жизни, то есть «популярные сайты становятся еще более популярными / богатые люди становятся еще более богатыми». Изначально модель копирования разрабатывалась для вычисления связанных между собой интернет-сообществ, в том числе и тех, что занимаются спамом, и ее основное отличие заключается именно в вероятностном присоединении новых вершин графа к уже существующим. В целом закон распределения уже обсуждался нами в прошлых материалах, посвященного детекции поискового спама, а более подробно про модели копирования можно узнать в [19]. Сейчас мы дадим определение для случайного графа: под RG = (V,P = (pij)) подразумевается граф с множеством вершин V, в котором ребра выпускаются случайно и независимо друг от друга, и для 1≤i, j≤|V| вероятность наличия ребра (vi,vj) составляет pij. Мы немного изменили оригинальное определение случайных графов, данное в [4] с учетом нашей ситуации. Обратите внимание на то, что каждый статичный граф может быть рассмотрен как особый случай случайного графа в том смысле, что pij может быть либо 0, либо 1. На таком случайном графе RG= (V,P), где P= (pij) является вероятностью существования ребра (vi,vj), ожидаемая температурная разница в узле i на временном интервале t + Δt и t будет соответствовать сумме ожидаемого тепла от всех предшественников, за вычетом того объема, которое он диффундирует своим последователям. Поскольку вероятность ссылки (vj,vi) составляет pji, ожидаемый поток тепла из узла j к узлу i следует умножить на вероятность pji; таким образом, мы имеем: fi(t+Δt)-fi(t)= -γfi(t)Δ+∑j:(uj,ui)∈Eγpijfj(t)Δt/RD+, где RD+(vi) ожидаемая полустепень исхода узла vi; это определяется как ∑kpik. Кроме этого:
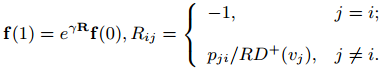
Для больших графов прямой подсчет eγR отнимает слишком много времени, воспользуемся дискретной аппроксимацией:
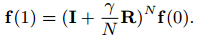
Матрицы (I+ γ/N R)N и eγR называются ядрами дискретной и непрерывной диффузии соответственно.
Страница материала:
Детекция поискового спама. Часть 1: Введение в алгоритм Google TrustRank
Детекция поискового спама. Часть 2: Расчет алгоритма Google TrustRank
Детекция поискового спама. Часть 3: От TrustRank к алгоритмам HostRank и DirRank
Детекция поискового спама. Часть 4: HostRank или PageRank, вычисляемый по графу хостов
Детекция поискового спама. Часть 5: От DirRank к алгоритму Truncated PageRank
Детекция поискового спама. Часть 6: Truncated PageRank и Вероятностный Подсчет
Детекция поискового спама. Часть 7: Знакомство с алгоритмом BadRank, обнуляющим Google PageRank
Детекция поискового спама. Часть 8: Google BadRank и ParentPenalty
Детекция поискового спама. Часть 9. Введение в алгоритм SpamRank
Детекция поискового спама. Часть 10: От исследования SpamRank к алгоритму Anti-TrustRank
Детекция поискового спама. Часть 11: Эксперименты с алгоритмом недоверия Anti-TrustRank
Детекция поискового спама. Часть 12: Применение принципов термодиффузионной
Детекция поискового спама. Часть 13: Детальный анализ алгоритма ранжирования DiffusionRank
Детекция поискового спама. Часть 14: Вычисление AIR на веб-графе, эквивалентного электронной схеме
Детекция поискового спама. Часть 15: Применение искусственных нейронных сетей
Полезная информация по продвижению сайтов:
Перейти ко всей информации