SEO-Константа
Яндекс.Директ + оптимизация
В предыдущих частях наших публикаций, посвященных детекции поискового спама, мы уже касались вопросов машинного обучения в задачах классификации страниц сайтов, как второго направления работ, связанных с улучшением качества поисковой выдачи. Ранее мы уже описывали вам результаты экспериментов по вычислению непотистских (кумовских) линков с использованием алгоритма построения деревьев решений C 4.5, а также занимались определением спамденсинга в блогах (сплогах) посредством машины опорных векторов (SVM). Конечно, мы не ставим пред собой глобальной задачи описать все возможные методы, позволяющие поисковым системам справляться с проблемой некачественных сайтов, как и рассказать вам обо всех манипулятивных технологиях, которые используются при их продвижении. Однако для приведения нашего справочного материала к относительно законченному виду, в его заключительной части нам бы хотелось немного поподробнее поговорить о применении искусственных нейронных сетей при обнаружении спамденсинга. Сейчас крупные поисковые системы, как Yahoo!, Bing и Яндекс достаточно активно используют машинное обучение при ранжировании сайтов в результатах органической выдачи. Например, на поиске Bing действует алгоритм RankNet, а на Яндексе — MatrixNet. В свою очередь корпорация Google пока что не готова полностью доверить свой поиск вышеуказанной технологии, что объясняется двумя причинами: во-первых, создатели текущего ранжирующего алгоритма Google уверены в том, что и их модель способна решать задачи более эффективно, нежели чем машинное обучение; во-вторых, интернет-гигант имеет небеспочвенные опасения касательно того, что новая модель ранжирования, созданная методами машинного обучения может повести себя непредсказуемо на тех классах запросов, которые существенно отличаются от обучающей выборки. [3] Вторая причина представляет для нас куда более значительный интерес, поскольку она не только восходит к такой известной проблеме индуктивной логики, сформулированной немецким математиком К.Г. Гемпелем и вступающей в противоречие с интуицией (утверждение «все вороны черные» логически эквивалентно тому, что «все нечерные предметы — не вороны»), но и заставляет нас вернутся к ряду нерешенных вопросов Ф.Розенблатта, создавшего первую в мире нейронную сеть, способную к перцепции и формированию отклика на воспринятый им стимул – однослойный персептрон [4]. Опираясь на критику элементарного персептрона Розенблатта, мы можем понять всю уязвимость данной рейтингующей модели, о который нам сообщают специалисты Google: способны ли искусственные системы обобщать свой индивидуальный опыт на широкий класс ситуаций, для которых отклик не был сообщен им заранее? Нет, индивидуальный опыт искусственных систем на практике всегда ограничен и никогда не является полным. Так или иначе, сейчас нашей первоочередной задачей является вычисление спамденсинга, а инструментарий машинного обучения позволяет решать ее с достаточно высокой степенью эффективности. Поэтому, давайте перейдем от общих проблем поиска к более конкретным, считая все вышеизложенное не более чем подготовкой к исследованию вопросов использования искусственных нейросетей в борьбе с поисковым спамом.
Поскольку в интернете существует огромное количество русскоязычной литературы, посвященной нейросетям, дальнейшие определения мы будем давать в сжатом виде, полагая, что при наличии живого интереса, наши читатели смогут ознакомиться с данными алгоритмами самостоятельно. Под искусственной нейронной сетью понимают параллельную и распределенную вычислительную структуру, состоящую из взаимосвязанной совокупности нейронных элементов. В математической модели нейрона вектор входных сигналов преобразуется в выходной сигнал посредством прохождения через блок локальной памяти (содержит данные о синоптических весах), блок суммирования (текущее состояние нейрона определяется как взвешенная сумма синоптических весов) и, наконец, блок преобразования. Важной характеристикой нейронной сети является возможность ее обучения, которое может осуществляться как с учителем, без супервизора, а также их комбинирование. Под обучением нейросети мы подразумеваем последовательную настройку ее архитектуры и синоптических весов для эффективного выполнения поставленных перед нею задач. Соответственно, в том случае, если мы говорим об обучении с учителем, супервизору известны правильные ответы заранее, а подстройка синоптических весов выполняется таким образом, чтобы минимизировать ошибку. Обучение без учителя заключается в категоризации без вмешательства супервизора, посредством исследования внутренней структуры данных. В качестве обобщения однослойного персептрона Розенблатта, о котором мы писали чуть выше, выступает многослойный персептрон (MLP), предложенный Румельхартом и МакКлелландом. Он состоит из группы входных элементов, образующих входной слой; одного или нескольких промежуточных (скрытых) слоев и одного выходного слоя. См. Рис. 69
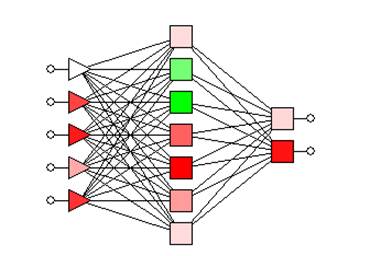
Рис. 69. Пример многослойного персептрона
Поскольку значения выходов для нейронов промежуточных слоев нам не известны, при обучении с учителем многослойного персептрона мы используем алгоритм обратного распространения ошибок: сигналы распространяются прямо по иерархии от низших слоев к высшим, а распространение ошибок следует в обратном направлении. В [7] говорится, что наиболее распространенным критерием остановки при обучении многослойного персептрона, как и других типов искусственных нейронных сетей, является максимально допустимое количество итерации, но оно также может завершаться и при достижении минимальной полной ошибки. Несмотря на всю свою эффективность, алгоритм обратного распространения ошибок отличается крайне долгим процессом обучения, а в некоторых сложных задачах может вообще оказаться неспособным к обучению. В свою очередь такие алгоритмы второго порядка, как метод Левенберга-Маркара [8], [9], [10], могут существенно ускорить работу. В отличие от алгоритмов требующих супервизора, самоорганизующаяся карта Кохонена (SOM) представляет собой соревновательную нейросеть с обучением без учителя, то есть она учится понимать саму структуру данных, обучаясь методом последовательных аппроксимаций. Основной целью самоорганизации является адаптивное, топологически упорядоченное преобразование входных векторов весов, обладающих произвольной размерностью, в одномерную и/или двухмерную карту [7,11]. См. Рис. 70
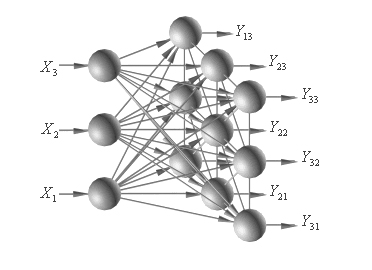
Рис. 70. Пример самоорганизующейся карты
Однако у самоорганизации есть один существенный изъян, который заключается в том, что те классы, которые они выделяют, не зависят от пользовательских предпочтений. Поэтому, далее нам потребуется квантизация обучающих векторов (LVQ), то есть после соревнующегося слоя мы добавляем линейный слой, обучающийся реакции на определенные классовые комбинации, создаваемых слоем соревнования. Таким образом, полученная квантизационная сеть представляет собой гибрид, использующий как обучение с учителем, так и без него. Наконец, нейронная сеть радиальных базисных функций (RBF), в наиболее частой форме, содержит три слоя, а именно: входной (содержит в себе сенсорные элементы, связывающие нейросеть с внешней средой), скрытый промежуточный (состоит из радиальных базисных функций, воспроизводящих гауссову поверхность перцепции и выполняющих нелинейное преобразование пространства входа) и единственный выходной (содержит нейроны с линейными функциями активации), который выполняет преобразование пространства промежуточного слоя.[7]
Прежде мы мало акцентировались на методах обнаружения контентного спама, мотивируя это тем, что основной целью текущих публикаций является фокусировка на ссылочных алгоритмах. Как вы сами прекрасно понимаете, продвижение сайтов даже сейчас пытается использовать приемы и техники, нацеленные на содержимое документа [2], однако на текущем этапе развития поиска, такой вид спама идентифицируется достаточно эффективно по сравнению с ссылочными практиками. Поэтому, создавая интернет-сайт, прежде всего, думайте не о поисковых машинах, агентах накопления данных, индексе цитирования, авторитетности, формулах ранжирования и т.д., а о своих пользователях, которые, как и вы сами, являются живыми людьми и стремятся получить не только исчерпывающий, но и честный ответ на свой вопрос. Дальнейшие эксперименты по вычислению спама проводились на публичной коллекции WEBSPAM-UK2006 (Yahoo! Research: «Web Spam Collections»), которая включала в себя 105,896,555 документов, расположенных на 114,529 хостах, относящихся к доменной зоне UK. Для классификации хостов на качественные и те, что ассоциируются с поисковым спамом, мы использовали набор, включающий 8,487 векторов признаков. Каждый вектор был составлен из 96 характеристик, предложенных в [6], где 24 извлекались из домашней страницы хоста, 24 — из страниц с самым высоким Google PageRank, 24 представляли собой математическое ожидание данных величин по всем документам, а оставшиеся 24 – его дисперсию. В том случае, если мы не могли однозначно классифицировать хост (неопределенно), связанные с ним векторы признаков не учитывались. Для автоматического обнаружения поискового спама на основании особенностей содержимого цифровых документов, были использованы следующие алгоритмы: многослойный персептрон, обученный методами градиентного спуска и Левенберга –Маркара; самоорганизующаяся карта Кохонена с квантизацией обучающих векторов и сеть радиальной базисной функции. Все искусственные нейронные сети были реализованы с одним скрытым слоем и единственным нейроном в выходном. Кроме этого, была использована линейная функция активации в выходном слое, а в промежуточном — активационная функция гиперболического тангенса. Таким образом, мы задаем начальные значения синоптических весов и сетевых смещений (осуществляется инициализация искусственной нейросети) в случайном диапазоне от -1 до +1, и нормализуем данные на этом интервале. Требуемый выход: -1 (качественный хост) или +1 (спам-документ). Тогда, для многослойного персептрона и радиальной базисной функции, в том случае, если выходные значения больше или равны 0, хост оценивается как спам; в противном случае — качественный документ. Этого не происходит на картах самоорганизации, поскольку здесь нейроны помечаются смысловыми метками. Что же касается параметров, то мы используем следующие критерии остановки (за исключением сети радиальной базисной функции): максимальное число итераций больше предельно допустимого порогового значения θ; средний квадрат отклонения (MSE) обучающей выборки меньше предельно допустимого порогового значения γ или возрастает среднеквадратическая ошибка валидационного множества (используется для проверки предсказательной способности модели) по истечению каждых 10 итераций. Все нижеперечисленные параметры, которые использовались в каждой модели искусственной нейронной сети, были эмпирически откалиброваны:
Для оценки производительности задействованных в данном исследовании алгоритмов мы подсчитываем среднеарифметическое, а также стандартное отклонение следующих оценочных метрик: аккуратность (Acc%), спам-полнота (Rcl%), специфичность (Spc%), спам-точность (Pcs%), F-мера (FM). См. Табл. 20
| MLP+Градиентный спуск | MLP+Левенберг-Маркар | RBF | SOM+LVQ | |
| Аккуратность | 86.2±1.2 | 88.6±1.4 | 79.7±0.6 | 80.6±0.8 |
| Полнота | 57.0±4.6 | 69.3±4.2 | 26.7±2.8 | 29.2±2.6 |
| Специфичность | 95.0±0.4 | 94.2±1.2 | 95.8±0.7 | 96.3±0.6 |
| Точность | 77.5±2.7 | 77.6±4.6 | 65.8±3.3 | 70.4±4.0 |
| F-мера | 0.656±0.039 | 0.731±0.032 | 0.379±0.030 | 0.412±0.030 |
Таблица 20 описывает показатели эффективности каждой искусственной нейронной сети. Согласно полученным данным многослойный персептрон, обученный методом Левенберга–Маркара, достигает наилучших результатов. С другой стороны, самоорганизующаяся карта Кохонена с квантизацией обучающих векторов и искусственная сеть радиальной базисной функции показали крайне плохую производительность с очень низким показателем полноты. Кроме того, во всех результатах мы отмечаем высокие показатели специфичности при крайне незначительном показателе спам-полноты, что косвенно указывает нам на то, что текущие классификаторы более успешны при идентификации качественных хостов, а не спам документов. Пытаясь понять причину получения подобного рода результатов, мы выдвинули гипотезу, касательно наличия избыточной размерности векторов признаков, которая может влиять на производительность классификации. Исходя из этого, мы используем метод главных компонент (PCA) [7] для анализа и последующего уменьшения размерности пространства признаков с минимальной потерей информации. Было обнаружено, что потенциально лишь 23 размерности вмещают в себя порядка 99% всей информации, содержащихся в исходных 96 векторах признаков. Согласно анализу, наиболее релевантная информация соответствует первым 21 размерностям. Таким образом, можно сделать вывод о том, что для классификации хоста нам достаточно извлечения только тех атрибутов, которые относятся к его домашней странице. После уменьшения размерности (с 96 до 23 признаков), мы выполнили новое моделирование, результаты которого отражены в Таблице 21:
| MLP+Градиентный спуск | MLP+Левенберг-Маркар | RBF | SOM+LVQ | |
| Аккуратность | 81.0±0.6 | 85.5±1.5 | 76.9±0.4 | 77.3±0.2 |
| Полнота | 38.8±2.4 | 55.5±3.4 | 2.5±1.3 | 3.1±0.8 |
| Специфичность | 95.1±0.6 | 94.8±1.2 | 99.5±0.3 | 99.8±0.1 |
| Точность | 71.1±2.8 | 77.0±4.0 | 58.6±19.8 | 88.3±6.5 |
| F-мера | 0.502±0.024 | 0.644±0.027 | 0.047±0.024 | 0.060±0.014 |
Опираясь на данные, приведенные в Таблице 21, можно увидеть, что вопреки тому обстоятельству, что новые векторы признаков включали в себя более чем 99% всей исходной информации, понижение размерности пространства признаков достаточно негативно отразилось на производительности всех наших классификаторов. Это особенно заметно на самоорганизующихся картах Кохонена и нейросети радиальной базисной функции, которая достигает полноты спама на уровне 5%. Теперь мы подозреваем, что наблюдаемый высокий показатель специфичности при одновременно низком показателе полноты, заключается в том, что количество качественных хостов превалирует над числом спам-страниц. Поэтому на этапе следующего обучения алгоритмов объем данных в двух классах будет одинаков. См. Табл. 22
| MLP+Градиентный спуск | MLP+Левенберг-Маркар | RBF | SOM+LVQ | |
| Аккуратность | 84.7±1.6 | 87.6±1.5 | 63.6±1.3 | 66.9±0.7 |
| Полнота | 82.9±2.0 | 86.5±2.0 | 45.6±1.9 | 59.7±5.9 |
| Специфичность | 86.4±2.4 | 88.8±1.9 | 81.6±1.5 | 74.2±5.5 |
| Точность | 86.1±2.4 | 89.1±2.4 | 71.3±2.1 | 70.1±2.9 |
| F-мера | 0.845±0.015 | 0.877±0.017 | 0.556±0.016 | 0.642±0.026 |
Анализируя полученные результаты можно заметить, что в том случае, если обучение искусственных нейронных сетей производится на классах с одинаковым числом образцов в каждом, мы существенно повышаем производительность всех наших классификаторов. При сравнении новых данных с той информацией, которая содержится в Табл. 20 видно, что при увеличении полноты, здесь мы имеем и несколько пониженное значение специфичности, по сравнению с прошлыми результатами. Однако F-мера, которая объединяет в себе метрики точности и полноты, в Табл. 22 также увеличилась по всем нашим алгоритмам. Для того, чтобы доказать вам целесообразность применения искусственных нейросетей при обнаружении некачественных страниц, мы решили сравнить описанную в текущем исследовании методологию с наиболее успешными результатами, которые были достигнуты с использованием прочих методов классификации. См. Табл. 23
| Классификаторы | Pcs | Rcl | FM |
| Деревья решений [6] — содержимое | — | — | 0.683 |
| Деревья решений [6] — содержимое + линки | — | — | 0.763 |
| Машина опорных векторов [1] — содержимое | 60.0 | 36.4 | — |
| Беггинг [5] — содержимое | 84.4 | 91.2 | — |
| Беггинг [5] — содержимое | 86.2 | 91.1 | — |
| MLP+Градиентный спуск — содержимое | 86.1 | 82.9 | 0.845 |
| MLP+Левенберг-Маркар — содержимое | 89.1 | 86.5 | 0.877 |
| RBF — содержимое | 88.3 | 45.6 | 0.556 |
| SOM + LVQ — содержимое | 64.2 | 59.7 | 0.642 |
Сравнительный анализ показывает, что многослойный персептрон, обученный методом Левенберга–Маркара, оказывается весьма конкурентоспособным, а потому может служить вполне эффективным инструментом для решения поставленных перед нами задач. Вопреки тому, что метрика полноты при использовании алгоритма беггинга (bagging — от англ. bootstrap aggregating) из [5] достигает 91.2, что значительно выше нашего показателя, его точность ниже, а следовательно, и специфичность тоже. Кроме того, результаты показывают, что MLP оказывается значительно лучше алгоритмов построения деревьев решений [6] и метода опорных векторов [1].
Страница материала:
Детекция поискового спама. Часть 1: Введение в алгоритм Google TrustRank
Детекция поискового спама. Часть 2: Расчет алгоритма Google TrustRank
Детекция поискового спама. Часть 3: От TrustRank к алгоритмам HostRank и DirRank
Детекция поискового спама. Часть 4: HostRank или PageRank, вычисляемый по графу хостов
Детекция поискового спама. Часть 5: От DirRank к алгоритму Truncated PageRank
Детекция поискового спама. Часть 6: Truncated PageRank и Вероятностный Подсчет
Детекция поискового спама. Часть 7: Знакомство с алгоритмом BadRank, обнуляющим Google PageRank
Детекция поискового спама. Часть 8: Google BadRank и ParentPenalty
Детекция поискового спама. Часть 9. Введение в алгоритм SpamRank
Детекция поискового спама. Часть 10: От исследования SpamRank к алгоритму Anti-TrustRank
Детекция поискового спама. Часть 11: Эксперименты с алгоритмом недоверия Anti-TrustRank
Детекция поискового спама. Часть 12: Применение принципов термодиффузионной
Детекция поискового спама. Часть 13: Детальный анализ алгоритма ранжирования DiffusionRank
Детекция поискового спама. Часть 14: Вычисление AIR на веб-графе, эквивалентного электронной схеме
Детекция поискового спама. Часть 15: Применение искусственных нейронных сетей
Материал «Детекция поискового спама» подготовил и перевел Константин Скоморохов
Полезная информация по продвижению сайтов:
Перейти ко всей информации