SEO-Константа
Яндекс.Директ + оптимизация
Рассмотрим следующую задачу по рекомендации фильма, которую иногда называют проблемой «совместной фильтрации» (Hill и др., 1995, Shardanand и Maes, 1995). В этой задаче, новый пользователь, Алиса, ищет рекомендации по выбору фильмов, которые она, скорее всего, просмотрела бы с огромным удовольствием. Система совместной фильтрации сначала просит Алису отранжировать фильмы, которые она уже видела. Затем система анализирует рейтинги фильмов, предоставленные другими пользователями, и использует эту информацию, чтобы вернуться к списку рекомендуемых фильмов Алисы. Для этого, рекомендательная система ищет пользователей, чьи предпочтения схожи с Алисиными, и сочетает их предпочтения, чтобы предложить свои рекомендации.
В данной работе мы представим и изучим эффективный алгоритм обучения под названием RankBoost для объединения нескольких рейтингов или предпочтений (мы используем эти термины как взаимозаменяемые). Данный алгоритм основан на алгоритме AdaBoost и его недавней альтернативной версии, разработанной Шепиром и Зингером (1999). Как и в других алгоритмах усиления, RankBoost работает путем объединения многих «слабых» рейтингов заданных примеров. Каждый из них может только слабо коррелироваться с заданным рейтингом, к которому мы пытаемся приблизиться. Мы покажем, как объединить такие слабые рейтинги в единый высокоточный рейтинг.
Мы изучим проблему ранжирования в общем фреймворке обучения. Грубо говоря, цель алгоритма обучения состоит в том, чтобы просто получить единое линейное упорядочение заданного набора объектов путем объединения набора заданного линейного упорядочения, известного как признак ранжирования. В качестве обратной связи, алгоритму обучения предоставляется информация о том, какие пары объектов должны ранжироваться выше или ниже относительно друг друга. Алгоритм обучения затем пытается найти комбинированный рейтинг, что изменяет порядок расположения как можно меньшего количества пар, по отношению к данной обратной связи.
Далее мы подробно опишем RankBoost и докажем его эффективность на обучающем наборе. Мы также опишем эффективную реализацию «двусторонней обратной связи», частного случая, который естественным образом встречается во многих областях. Мы проанализируем сложность всех изученных алгоритмов.
Затем мы опишем эффективную процедуру поиска слабых рейтингов, которую планируем сочетать с RankBoost, используя признаки ранжирования. Например, при выполнении задачи с подбором фильма, эта процедура приводит к использованию очень простых слабых рейтингов, что разделяет все фильмы только на два эквивалентных множества: те, которые являются более предпочтительными и те, которые являются менее предпочтительными. В частности, мы используем ранжированный список другого зрителя фильмов, распределенный в зависимости от того предпочитает он конкретный фильм или нет, что находится в его списке. Такое деление данных имеет то преимущество, что оно зависит только от относительного упорядочения, определенного заданными рейтингами, а не абсолютными. Другими словами, даже если рейтинг фильмов выражается путем присвоения каждому фильму числового значения, мы игнорируем его и сосредотачиваемся только на их относительном порядке. Это различие становится очень важным, когда мы объединяем рейтинги от многих зрителей, которые часто используют совершенно разные диапазоны баллов, чтобы выразить одинаковые предпочтения. Ситуации, в которых мы должны объединить рейтинги различных моделей, также возникают в задачах систем метапоиска (Etzioni и соавт., 1996) и в информационно-поисковых задачах (Salton, 1989, Salton и McGill, 1983).
Далее для конкретного вероятностного набора, мы изучим обобщенные результаты RankBoost, то есть, ожидаемые результаты, которые не проявились во время эксперимента. Этот анализ основан на теореме о равномерной сходимости, которую мы докажем относительно результатов, полученных на обучающей выборке с ожидаемым выполнением на отдельной тестовой выборке.
Также мы приведем результаты экспериментальных испытаний нашего подхода на двух разных задачах. Первой является задача метапоиска. Цель данного поиска состоит в объединении рейтингов нескольких стратегий веб поиска. Каждая стратегия поиска является операцией, которая, используя запрос в качестве входных данных, выполняет некоторое простое преобразование запроса (например, добавление поисковых директив, таких как «и» или поиска таких токенов, как, например, «домашняя страница») и отправляет его к конкретной поисковой системе. Результатом работы каждой стратегии является упорядоченный список URL-адресов, которые предложены в качестве ответов на запрос. Цель состоит в том, чтобы объединить стратегии, которые лучше всего подходят для данного набора запросов.
Второй является задача выбора фильма, описанная выше. Для нее существует большой общедоступный набор данных, содержащий рейтинги фильмов от разных людей. Мы сравнили RankBoost с алгоритмом ближайшего соседа и алгоритмом регрессии, которые были ранее изучены для данной задачи, используя ряд методов оценивания. RankBoost показал себя явным победителем в этих экспериментах.
В дополнение к экспериментам, о которых мы говорили, Collins (2000) и Walker, Rambow и Rogati (2001) описали эксперименты с использованием алгоритма RankBoost для задач обработки естественного языка. Кроме того, в одной работе (Iyer и др., 2000), сравнили две версии RankBoost с традиционными информационно-поисковыми подходами.
Несмотря на широкий спектр применения, который использует и сочетает ранжирование, этой проблеме уделялось относительно мало внимания в области машинного обучения. Некоторые методы, что были разработаны для объединения рейтингов, как правило, основаны либо на методах ближайшего соседа (Resnick и др., 1995, Shardanand и Maes, 1995) или методах градиентного спуска (Bartell с соавт., 1994, Caruanaи др., 1996). В последнем случае рейтинги рассматриваются как вещественные величины, и задача объединения различных рейтингов сводится к численному поиску набора параметров, которые сведут к минимуму разрыв между объединенными значениями рейтингов и обратной связью с пользователем.
Хотя приведенные выше (и другие) подходы могут хорошо работать на практике, они все еще не гарантируют, что комбинированная система будет соответствовать предпочтениям пользователя, когда мы рассматриваем значение рейтингов в качестве средства выражения предпочтений. Cohen, Schapire и Singer (1999) предложили фреймворк для обработки и объединения нескольких рейтингов для того, чтобы непосредственно минимизировать количество расхождений. В их основе рейтинги используются для построения графа предпочтений, и задача сводится к комбинаторной задаче оптимизации, которая оказывается NP-полной. Поэтому используется аппроксимация для объединения различных рейтингов. Они также описывают эффективный онлайновый алгоритм для смежной проблемы.
Наш алгоритм использует аналогичную структуру, что и в работе Cohen, Schapire и Singer, но позволяет избежать трудности обработки. Кроме того, в отличие от их онлайнового алгоритма, RankBoost больше подходит для групповых наборов, когда есть достаточно времени, чтобы найти хорошую комбинацию. Таким образом, эти два подхода дополняют друг друга. Вместе, эти алгоритмы являются эффективным методом объединения нескольких рейтингов, что, как наши эксперименты показывают, очень хорошо работает на практике.
В этом разделе мы опишем нашу формальную модель для изучения ранжирования. Пусть X будет множеством, которое назовем пространством определения. Элементы X называются экземплярами. Это объекты, которые нас интересуют в ранжировании. Например, в задаче ранжирования фильмов, каждый фильм является экземпляром.
Наша цель состоит в объединении заданного набора предпочтений или рейтингов экземпляра пространства. Мы используем признак ранжирования для обозначения заданных рейтингов этих экземпляров. Признак ранжирования является не более чем упорядочением экземпляров от наиболее предпочитаемых до наименее предпочитаемых. Чтобы сделать модель гибкой, мы позволим связать эту упорядоченность, и мы не требуем, чтобы все экземпляры ранжировались по каждому признаку.
Будем считать, что алгоритм обучения в нашей модели задается n признаками ранжирования, обозначаемыми
f1,…, fn. Поскольку каждый признак fi определяет линейное упорядочение экземпляров, мы
можем эквивалентно представить себе fi как функцию значений, где более высокие значения назначаются более
предпочтительным элементам. То есть, мы можем представить любой признак ранжирования как действительную функцию, где
fi(x1) >fi(x0) означает, что экземпляр x1 предпочитается
x0 по fi. Фактические числовые значения fi несущественны; нас интересует только упорядочение,
которое они определяют. Обратите внимание, что это представление также позволяет объединять экземпляры (так как fi
может назначить одинаковые значения в двух экземплярах).
Как отмечалось ранее, часто бывает удобно разрешить функции ранжирования fi «воздержаться» от конкретного
экземпляра. Чтобы представить такое воздержание на конкретном экземпляре х, мы просто присваиваем fi(x) специальный
символ ⊥, который не сопоставляется со всеми действительными числами. Таким образом, fi(x) = ⊥ указывает,
что рейтинг не задается х на fi. Формально, что каждый признак ранжирования fi является функцией в виде
fi: X → R—, где множество R— состоит из действительных чисел и дополнительного
элемента ⊥.
Признаки ранжирования предназначены для обеспечения предельного уровня детализации задачи ранжирования. Иначе говоря, работа обучаемого будет состоять в том, чтобы изучить выражение ранжирования относительно исходных признаков ранжирования, аналогичных обычным признакам в более традиционных обучающих наборах. (Тем не менее, мы решили назвать их «признаками ранжирования», а не просто «признаками», чтобы подчеркнуть, что они имеют особую форму и функцию).
Например, в одной постановке задачи по выбору фильма, каждый признак ранжирования соответствует прошлым рейтингам одного из зрителей фильмов, так что существует столько признаков ранжирования, сколько имеется пользователей. Фильмам, которые были оценены зрителем, назначаются числовые значения оценки зрителя фильма; фильмам, которые не были вообще оценены зрителем, присваивается специальный символ ⊥, чтобы указать, что фильм не имеет рейтинга. Таким образом, fi(x) является числовым значением рейтинга «фильм-зритель» фильма х или ⊥, если он не был оценен.
Целью обучения является объединение всех функций ранжирования, в единый рейтинг экземпляров, который называется окончательным или комбинированным рейтингом. Окончательный рейтинг должен иметь тот же вид, что и признаки ранжирования, то есть, он должен иметь линейное упорядочение экземпляров (с разрешением объединения). Однако, в отличие от признаков ранжирования, мы не разрешаем окончательному рейтингу воздержаться на каких-либо экземплярах, так как мы хотим иметь возможность ранжировать все экземпляры, даже те, которые не встречались во время испытания. Таким образом, формально окончательное ранжирование может быть представлено в виде функции H: X → R с интерпретацией подобно признакам ранжирования, т. е. x1 ранжируется выше, чем х0 по Н, если H(x1) >H(x0). Обратите внимание на явное упущение ⊥ из диапазона H, что запрещает воздержания. Например, для выполнения задачи выбора фильма, это соответствует полному упорядочению всех фильмов (с разрешением объединения), где наиболее рекомендуемые фильмы наверху упорядоченного списка имеют самые высокие значения рейтинга.
Наконец, необходимо предположить, что обучающийся имеет некоторую информацию обратной связи, описывающую ожидаемую форму окончательного рейтинга. Обратите внимание, что эта информация не кодируется признаками ранжирования, которые являются лишь примитивными элементами, с которыми обучающийся создает свой окончательный рейтинг. В традиционной обучающей классификации эта обратная связь будет принимать форму метки на примерах, которые отображают правильную классификацию. Здесь наша цель состоит в том, чтобы придумать хороший рейтинг экземпляров, так что нам необходима некоторая обратная связь, например, для того, что бы понять, что это означает для ранжирования быть «хорошим».
Один естественный способ представления такой обратной связи будет в той же форме, что и признак ранжирования, т. е. в виде линейной упорядоченности всех экземпляров (с разрешением объединения и воздержания). Цель учащегося затем может заключаться в том, что бы построить окончательный рейтинг, который построен из признаков ранжирования и который является «подобным» (по некоторому соответствующему определению подобия) заданному рейтингу обратной связи. Эта модель будет отличной, например, для задачи ранжирования фильмов, поскольку целевой зритель, Алиса, задает рейтинги всем фильмам, которые она видела, — информацию, которую можно легко преобразовать в рейтинг обратной связи таким же образом, как преобразовать рейтинги от других пользователей в признаки ранжирования.
Однако в других областях, эта форма и представление информации обратной связи могут быть чрезмерно ограниченными. Так, в некоторых случаях, два экземпляра могут полностью быть несвязанными, и мы можем не заботиться о том, как они соотносятся. Предположим, например, что мы пытаемся ранжировать отдельные кусочки фруктов. Мы можем иметь только информацию о том, как сравнить отдельные яблоки с другими яблоками, и как апельсины сравнить с апельсинами, но мы не могли бы сравнить яблоки и апельсины. Более реалистичный пример задается задачей метапоиска.
Другая трудность линейного упорядочения обратной связи состоит в том, что мы можем считать, что важнее (из-за совокупности данных) ранжировать экземпляр x1 выше х0, но менее важно, ранжировать экземпляр x2 выше x3. Такие вариации важности того, как экземпляры ранжированы друг с другом, не могут быть легко представлены с использованием простого линейного упорядочения экземпляров. Чтобы разрешить кодирование такой общей информации обратной связи, мы вместо этого считаем, что обучающийся получает информацию об относительном рейтинге отдельных пар экземпляров. То есть, для каждой пары экземпляров x0, x1 обучающийся имеет информацию о том, следует ли ранжировать x1 выше или ниже х0, а также, насколько важно или насколько сильны доказательства того, что этот рейтинг должен существовать. Вся эта информация может быть удобно представлена одной функцией Φ. Областью Φ являются все пары экземпляров. Для любой пары экземпляров x0, x1, Φ (x0, x1) является вещественным числом, знак указывает на то, должен ли x1 быть ранжированным выше х0, величина которого представляет важность в данном ранжировании.
Формально мы предполагаем, что функция обратной связи имеет такой вид Φ : X x X → R. Здесь Φ(x0,x1) > 0 означает, что x1 должен быть ранжирован выше х0, а Φ(x0,x1) < 0 означает обратное. Нулевое значение указывает на отсутствие предпочтения между x0 и x1. Как отмечалось выше, чем больше величина |Φ(x0,x1)|, тем более важно ранжировать x1 выше или ниже х0. В соответствии с этой интерпретацией, мы предполагаем, что Φ(x,x) = 0 для всех x∈X, и что Φ является антисимметричным в том смысле, что Φ(x0,x1) = −Φ(x1,x0) для всех x0,x1∈X. Заметим, однако, что мы не предполагаем транзитивности функции обратной связи (На самом деле, мы даже не использовали свойство антисимметричности Φ, так что это условие также может быть опущено. Например, мы могли бы вместо этого формализовать Φ в виде неотрицательной функции, в которой положительное значение Φ(x0,x1) указывает на то, что x1 должен быть ранжирован выше, чем х0, но нет ограничения на то, чтобы Φ(x0,x1) и Φ(x1,x0) были положительными. Это может быть полезным, если у нас есть противоречивые сведения относительно «истинного» рейтинга x0 и x1 и классификации обучения, когда те же экземпляры появляются дважды в одной обучающей выборке с разными метками).
Например, для выполнения задачи ранжирования фильмов, мы можем определить Φ(x0,x1) как +1, если Алисой фильм x1 был предпочтен фильму х0, как -1, если было наоборот, и как 0, если любой из фильмов не был просмотрен или если бы они были оценены в равной степени.
Как было отмечено выше, алгоритм обучения, как правило, пытается найти окончательный рейтинг, который похож на заданную функцию обратной связи. Существует, возможно, много способов измерения такого сходства. В данной работе мы сосредотачиваем внимание на минимизации (взвешенного) числа пар экземпляров, порядок которых изменен окончательным рейтингом относительно функции обратной связи. Для формализации этой цели, пусть D(x0,x1) = c⋅max{0,Φ(x0,x1)} так, что все негативные элементы Φ (которые не несут никакой дополнительной информации) приравниваются нулю. Здесь с является положительной константой и выбирается так, что
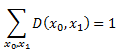
(Если не указан определенный диапазон суммирования, мы всегда считаем, что нужно суммировать все элементы X). Определим пару x0,x1 как решающее значение, если Φ(x0,x1) > 0 так, что пара получает отличный от нуля вес под D.
Алгоритмы обучения, которые мы изучаем, пытаются найти окончательный рейтинг H с небольшим взвешенным числом решающих пар беспорядочных элементов. Эта величина, называется рейтингом потери и обозначается как rlossD(H). Формально рейтинг потери определяется как
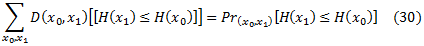
Вот и в этой статье, мы используем обозначение [[π]], которое определяет равенство 30, если соблюдается условие π, и 0 в противном случае. Есть много других способов измерения окончательного рейтинга. Некоторые из них мы рассмотрим в этой работе.
Конечно, реальная цель обучения заключается в создании рейтинга, который работает хорошо, даже на экземплярах, которые не наблюдались в процессе испытания. Например, для выполнения задачи ранжирования фильмов, мы хотели бы найти рейтинг всех фильмов, который точно бы предвидел, какие фильмы будут нравиться зрителю больше или меньше, чем другие. Очевидно, этот рейтинг имеет значения только для фильмов, которые зритель еще не смотрел. Как и в других условиях обучения, хорошая работа системы обучения с данными не просмотренных фильмов зависит от многих факторов, таких как количество экземпляров, охваченных в испытании, и сложность представления ранжирования производимого учащимся. Некоторые из этих вопросов рассматриваются в данной работе.
При изучении сложности наших алгоритмов, будет полезным определить различные наборы и количества, которые измеряют размер вводимой функции обратной связи. Прежде всего, мы обычно предполагаем, что носитель Φ является конечным. Пусть XΦ обозначает множество экземпляров обратной связи, то есть, тех экземпляров, которые встречаются в носителе Φ:
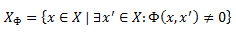
Кроме того, пусть |Φ| будет размером носителя Φ:
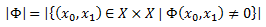
В некоторых ситуациях, таких как задача метапоиска, целесообразным для обучающегося будет принятие набора функций обратной связи Φ1,…,Φm. Тем не менее, все они могут быть объединены в одной функции Φ простым их прибавлением: Φ = ∑jΦj. (Если некоторые из них имеют большее значение, чем другие, то может быть использована взвешенная сумма).
Чтобы проиллюстрировать эту модель, опишем теперь задачу метапоиска и то, как она вписывается в общий фреймворк. Для решения этой задачи мы использовали данные Cohen, Schapire и Singer (1999). Их цель состояла в имитировании задачи построения урезанной системы информационного поиска. В качестве тестирования они выбрали два довольно узких класса запросы-извлечения домашних страниц исследователей машинного обучения (ML), и извлечения домашних страниц университетов (UNIV). Эти тестовые сценарии были выбраны отчасти потому, что обратная связь была легкодоступной в интернете. Они получили список исследователей машинного обучения, определённых по имени, и принадлежности к учреждению с их домашними страницами, и подобный список университетов, определенных по названию и (иногда) географическому положению в Yahoo! Мы ссылаемся на каждую запись в этих списках (т.е. на пару имя-учреждение или пару имя-место) в качестве базового запроса. Цель состоит в том, чтобы узнать стратегию метапоиска, которая, учитывая базовый запрос, будет генерировать ранжирование URL-адресов, которые бы содержали корректно определенную домашнюю страницу в начале или ближайшую к началу списка. Cohen, Schapire и Singer также создали ряд специальных шаблонов поиска для каждой области. Каждый шаблон определяет метод расширения запроса для преобразования базового запроса в подобный запрос AltaVista, который мы называем расширенным запросом. Например, один из шаблонов имеет вид +»ИМЯ» + машина + обучение, это означает, что AltaVista должна искать все слова в имени человека и слова «машина» и «обучение». При внесении в базовый запрос » исследователь Джо из лаборатории Шеннон во Флорам Парк» этот шаблон расширяется до расширенного запроса + » исследователь Джо » + машина обучение. В общей сложности 16 шаблонов поиска были использованы для области ML и 22 для области UNIV. Каждый шаблон поиска был использован для получения первых тридцати документов. Если ни один из этих списков не содержал правильной домашней страницы, то базовый запрос отбрасывали из эксперимента. В области ML было 210 базовых запросов, для которых, по крайней мере, один шаблон поиска дал правильную домашнюю страницу; для домена UNIV было 290 таких базовых запросов.
Мы отобразили проблему метапоиска в нашем фреймворке следующим образом. Формально экземплярами сейчас являются пары вида (q,u), где q является базовым запросом, а u — одним из URL-адресов, возвращенных одним из шаблонов поиска по этому запросу. Каждый признак ранжирования fi создается из соответствующего шаблона поиска i, назначенного j-ым URL u в своем списке (для базового запроса q) ранжирования − j, то есть fi((q,u)) = − j. Если u не ранжирован базовым запросом, то мы полагаем, что fi((q,u)) = ⊥. Мы также создаем отдельную функцию обратной связи Φq для каждого базового запроса q, который ранжирует правильный URL домашней страницы u∗ выше всех остальных. То есть, Φq((q,u),(q,u∗)) = +1 и Φq((q,u∗),(q,u)) = −1 для всех u≠u∗. Все остальные элементы из Φq равняются нулю. Все функции обратной связи Φq затем были объединены в одну функцию обратной связи Φ путем суммирования, как описано выше: Φ = ∑qΦq. Выходными данными алгоритма обучения является некоторый окончательный рейтинг H. В примере с метапоиском H является взвешенной комбинацией различных шаблонов поиска fi. Чтобы применить H, задавая тестовый базовый запрос q, мы сначала сформируем все расширенные запросы из шаблонов поиска и отправим их поисковой системе для получения списков URL-адресов. Затем мы оценим H на каждой паре (q,u), где u возвращается из URL, чтобы получить прогнозируемое ранжирование всех URL-адресов.
В этом разделе мы опишем подход к проблеме ранжирования на основе метода машинного обучения, который называется усилением, в частности AdaBoost алгоритм Freund и Schapire (1997) и его альтернативная версия, разработанная Schapire и Singer (1999). Усиление является способом получения высокоточных принципов прогнозирования путем объединения многих «слабых» принципов, которые могут быть лишь умеренно точными. В текущем режиме, мы используем усиление, чтобы получить функцию Н: X → R, упорядочение X которой будет приближаться относительному порядку, закодированному с помощью функции обратной связи Φ.
Мы называем наш алгоритм усиления — RankBoost, и его символичный код показан ниже. Как и все алгоритмы улучшения, RankBoost работает циклично. Мы допускаем доступ к отдельной процедуре, называемой слабым обучающимся (weak learner), которая на каждом цикле обязана генерировать слабый рейтинг. RankBoost поддерживает распределение Dt по X x X, которое происходит на цикле t к слабому обучающемуся. Интуитивно RankBoost выбирает Dt, чтобы подчеркнуть различные части данных обучения. Значительный вес, что присваивается паре элементов, указывает на большую важность того, что слабый обучающийся упорядочивает те пары правильно.

Рисунок 6. Алгоритм RankBoost
Слабые рейтинги имеют вид ht: X → R. Мы представляем их как предоставление информации ранжирования таким же образом, как признаки ранжирования и окончательный рейтинг. Слабый обучающийся, который использовался в наших экспериментах, основан на заданных признаках ранжирования; подробности приведены в следующем разделе.
Алгоритм усиления использует слабые рейтинги, чтобы обновить распределение, как показано на схеме. Предположим, что x0,x1 являются важнейшей парой, так что мы хотим, чтобы x1, был оценен выше, чем х0 (во всех остальных случаях, Dt будет равно нулю). Если предположить, что параметр αt> 0 (как этого и следует ожидать), то вес уменьшится Dt(x0,x1), если ht приведет правильное ранжирование ht(x1) > ht(x0), и вес увеличится в противном случае. Таким образом, Dt будет иметь тенденцию концентрироваться на парах, относительное ранжирование которых труднее всего определить. Фактическое значение αt будет обсуждаться далее.
Окончательный рейтинг Н является взвешенной суммой слабых рейтингов. В следующей теореме мы докажем ограничение рейтинга потерь для H. Эта теорема также дает представление о выборе αt и о создании слабого обучающегося, что мы и рассмотрим ниже на тренировочных данных. Как и в стандартной задаче классификации, потеря на отдельном тестовом наборе также может быть теоретически ограничена, учитывая соответствующие предположения с использованием теории равномерной сходимости (Bartlett, 1998, Haussler, 1992, Schapire и др., 1998, Vapnik, 1982). Далее мы выведем одно такое ограничение погрешности общего рейтинга Н и объясним, почему погрешность общей классификации трудно распространяется на параметры ранжирования.
Теорема 4. Принимая обозначение алгоритма RankBoost, рейтинг потери для H равняется
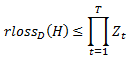
Доказательство: раскрывая правило обновления, мы получаем
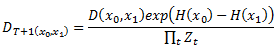
Обратите внимание, что [[x ≥ 0]] ≤ ex для всех действительных х. Таким образом, рейтинг потери по отношению к начальному распределению D равняется
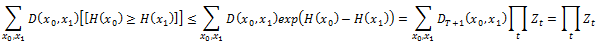
Это доказывает теорему. Обратите внимание, что наши методы выбора αt, которые представлены в следующем разделе, гарантируют, что Zt ≤ 1. Отметим также, что RankBoost, как правило, требует O(|Φ|) пространство и время за цикл.
В связи с ограничением, установленным в теореме 4, мы гарантированно производим сочетание рейтинга с низким рейтингом потерь, если на каждом цикле t мы выбираем αt, а слабый обучающийся создает ht для того, чтобы минимизировать Zt.
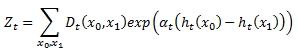
Формально RankBoost использует слабого обучающегося как «черный ящик» и не имеет никакого контроля над тем, как он выбирает свои слабые рейтинги. На практике, однако, мы часто сталкиваемся с задачей реализации слабого обучающегося, в этом случае мы можем создать его, чтобы минимизировать Zt.
Существуют различные методы для достижения данной цели. Здесь мы кратко рассмотрим три. Зафиксируем t и опустим все индексы t, если ясно из контекста. (В частности, в настоящее время, D будет обозначать Dt, а не начальное распределение).
Первый метод. Первый и наиболее обычный для любого заданного слабого рейтинга h. Можно показать, что Z, который рассматривается как функция от α, имеет единственный минимум, который можно найти численно посредством простого двоичного поиска (за исключением обычных вырожденных случаев).
Второй метод. Второй метод минимизации Z применяется в частном случае, когда h имеет диапазон {0,1}. В этом случае, мы можем минимизировать Z аналитически следующим образом: для b∈ {−1,0,+1}, пусть
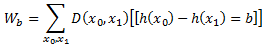
Кроме того, сократим W+1 по W+ и W−1 по W−.Тогда Z =W−e−α+W0+W+eα. Используя простое исчисление, можно проверить, что Z сводится к минимуму, полагая, что
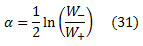
что дает:
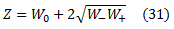
Третий метод. Для слабых рейтингов с диапазоном [0,1], мы можем использовать третий метод выбораα на основе аппроксимации к Z. В частности, в силу выпуклости eαx как функции от х, можно проверить, что
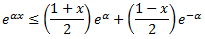
для всех вещественных α и х ∈ [-1, +1]. Таким образом, мы можем приблизить Z по
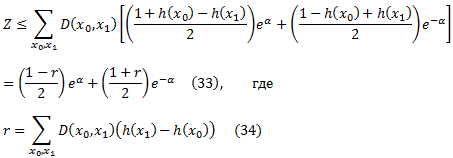
Правая часть уравнения (33) сводится к минимуму, если
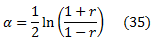
что, подставляя в уравнение (33) дает
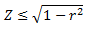
Таким образом, чтобы приблизительно минимизировать Z с помощью слабых рейтингов с диапазоном [0,1], можно попытаться максимизировать |r|, как определено в уравнении (34), а затем получить α из уравнения (35). Это метод, использовался в наших экспериментах.
Рассмотрим теперь случай, когда любой из этих трех методов полученияαприсваивает слабому рейтингу h вес α< 0. Например, в соответствии с уравнением (31), α является отрицательным, если W+, вес беспорядочных пар, больше, чем W—, вес правильно упорядоченных пар. Аналогично для уравнения (35), α< 0, если r< 0 (заметим, что r =W−−W+). Интуитивно это означает, что h отрицательно коррелируется с обратной связью; противоположное предположенное упорядочение будет лучше аппроксимироваться к обратной связи. RankBoost позволяет таким слабым рейтингам и их правилу обновления отображать эту интуицию: веса пар, которые h правильно упорядочивает, увеличиваются, а веса неправильно упорядоченных пар — уменьшаются.
В этом разделе мы опишем более эффективную реализацию RankBoost для обратной связи специального вида. Мы говорим, что функция обратной связи двудольная, если существуют непересекающиеся подмножества X0 и X1 для X так, что Φ ранжирует все экземпляры в X1 выше всех экземпляров в X0 и ничего не делает с какими-либо другими парами. То есть, формально, для всех x0∈X0 и всех x1∈X1 мы имеем, что Φ(x0,x1) = +1, Φ(x1,x0) = −1 и Φ равно нулю для всех остальных пар.
Такая обратная связь возникает естественным образом, например, в общих задачах ранжирования-поиска документов в области информационного поиска. Здесь, набор документов может считаться релевантным или нерелевантным. Функция обратной связи, которая кодирует эти предпочтения, будет двудольной. Цель алгоритма этой задачи заключается в выявлении соответствующих документов и представлении их пользователю. Вместо того чтобы классифицировать документы как релевантные или нерелевантные, наша цель состоит в том, чтобы получить ранжированный список всех документов, который пытается разместить все релевантные документы в начале списка. Одной из причин предпочтения ранжирования строгой классификации является то, что ранжирование выражает уверенность алгоритма в своих прогнозах. Другая причина заключается в том, что обычным пользователям ранжировано-поисковых систем не хватает терпения, чтобы исследовать каждый документ, который был предвиденный как релевантный, особенно если имеется большое количество таких документов. Ранжирование позволяет системе руководствоваться пользовательскими решениями о том, какие документы следует читать.
Результаты, представленные в этом разделе, могут касаться также того случая, когда функция обратной связи сама по себе не двудольная, но тем не менее может быть разложена как сумма двудольных функций обратной связи. Например, это имеет место в задаче метапоиска. Тем не менее, для простоты, мы опускаем полное описание этого непосредственного расширения и ограничим наше внимание на более простом случае.

Рисунок 7. Более эффективный вариант RankBoost для двудольной обратной связи
Если RankBoost реализуется наивно, то условия пространства и времени цикла будут O(|X0||X1|). В этом разделе мы покажем, как это может быть улучшено до O(|X0|+|X1|). Следует отметить, что в этом разделе, XΦ = X0∪X1. Основная идея заключается в поддержании набора весов vt по XΦ (а не распределения с двумя аргументами Dt), и поддержании состояния на каждом цикле
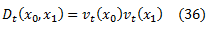
для всех ключевых пар x0,x1 (напомним, что Dt равно нулю для всех других пар).
Символичный код этой реализации показан на рисунке 7. Уравнение (36) можно доказать по индукции на t. Это ясно действует изначально. Используя наше предположение индукции, становится просто расширить вычисление Zt = Zt0⋅Zt1 на рисунке 7, чтобы увидеть, что это равносильно вычислению Zt на рисунке 6. Чтобы показать, что уравнение (36) имеет место на цикле t + 1, для решающей пары x0,x1 мы имеем
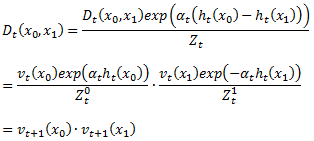
Наконец, обратите внимание, что все условия пространства и все вычисления по циклам равняются O(|X0| + |X1|), с возможным исключением вызова слабого обучающегося. К счастью, если мы хотим, чтобы слабый обучающийся максимизировал |r|, как в уравнении (34), то нам также необходимо только перенести |XΦ| веса на слабого обучающегося, которые можно вычислить по линейному времени в |XΦ|. Опуская t индексы, и определяя

Мы можем записать r как
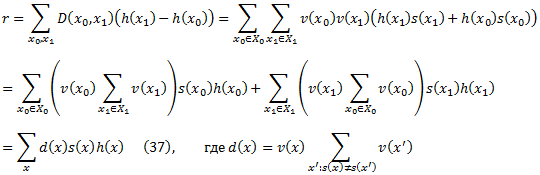
Все веса d(x) можно вычислить в линейном времени по первому вычислению суммы, которая появляется в этом уравнении для двух возможных случаев, когда x находится в X0 или X1. Таким образом, в этом случае нам нужно только передать |X0| + |X1|веса слабому обучающемуся, а не выполнять полное распределение Dt размера |X0| |X1|.
Как описано выше, нашему алгоритму RankBoost требуется доступ к слабому обучающемуся, чтобы создать слабые рейтинги. В этом разделе мы опишем эффективную реализацию слабого обучающегося для ранжирования. Возможно, самый простой и самый очевидный слабый обучающийся найдет слабый рейтинг h, который равен одному из признаков ранжирования fi, за исключением экземпляров без рейтинга. То есть,
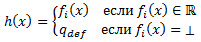
Для некоторых qdef∈ R.
Возможно, основной проблемой с таким слабым обучающимся является то, что она в значительной степени зависит от фактических значений, определенных признаками ранжирования, а не полагается исключительно на информацию относительной упорядоченности, которую те предоставляют. Мы считаем, что последние формулировки алгоритмов обучения будут более общими и практичными. Такие методы могут использоваться, даже если признаки ранжирования обеспечивают только упорядочение экземпляров и никакой числовой или другой информации не имеют. Такие методы также обходят вопрос объединения признаков ранжирования, общие значения которых имеют различную семантику (например, различные значения присваиваются URL-адресам различными поисковыми системами). По этим причинам, мы ориентируемся в этом разделе и в наших экспериментах на диапазон значений {0,1} для слабых рейтингов, которые используют информацию для упорядочения, предоставленную признаками ранжирования, но игнорируем конкретную информацию подсчета значения рейтинга. В частности, мы будем использовать слабые рейтинги h в виде
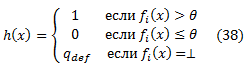
где θ∈R и qdef ∈ {0,1}. То есть, слабый рейтинг получают из признаков ранжирования fi путем сравнения его значений на заданном экземпляре к ограничениюθ. Для экземпляров, что остались без значений fi, слабый рейтинг присваивает значение по умолчанию qdef. Далее мы покажем, как выбрать «лучшие»: признак, ограничение и значение по умолчанию
Так как наши слабые рейтинги имеют диапазон значений {0,1}, для их поиска мы можем использовать второй и третий методы, описанные в предыдущем разделе. Мы выбрали третий способ, потому что мы можем реализовать его более эффективно, чем второй. Согласно второму способу, слабый обучающийся должен искать слабый рейтинг, который минимизирует уравнение (32). Для заданного потенциального слабого рейтинга, мы можем непосредственно вычислить величины W0, W−, и W+ за O(|Φ|) время. Кроме того, для каждого n признака ранжирования, существует по большей мере |XΦ| + 1 ограничения, которые стоит рассмотреть (как это определено диапазоном fi на XΦ) и два возможных значения по умолчанию (0 и 1). Таким образом, простая реализация второго метода требует O(n|Φ||XΦ|) времени, чтобы создать слабый рейтинг.
Третий метод требует максимизации максимально |r| в соответствии с уравнением (34) и имеет тот недостаток, что он основан на аппроксимации к Z. Хотя, простая реализация также требует O(n|Φ||XΦ|) времени, мы покажем, как это осуществить за O(n|XΦ|+|Φ|)время. (В случае двудольной обратной связи при использовании алгоритма усиления используется необходимо только O(n|XΦ|)времени). Это значительное улучшение с точки зрения наших экспериментов, в которых |Φ| имело значительные значения. Опишем время и пространство эффективного алгоритма для максимизации |r|. Зададим t и уберем его из всех индексов для упрощения обозначение. Начнем с того, что перепишем r для заданных D и h следующим образом:
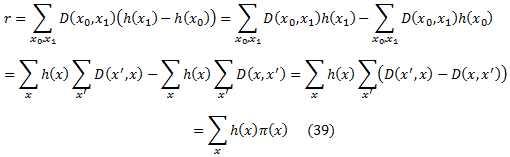
где мы определяем π(x) = ∑x’(D(x’,x) − D(x,x’)) как потенциал х. Обратите внимание, что π(х) зависит только от текущего распределения D. Таким образом, слабый обучающийся может предварительно вычислить все потенциалы в начале каждого цикла в O(|Φ|) времени и O(|XΦ|) пространстве. Если обратная связь двудольная, сравнивая уравнения (37) и (39), мы видим, что π(х) = d(x)s(х), где d и s определены в предыдущем разделе, таким образом, в этом случае, π может быть вычислено еще быстрее только за O(|XΦ|) время.
Теперь давайте приступим к задаче поиска хорошего порогового значения θ и значения по умолчанию qdef. Нам необходимо найти подходящие признаки ранжирования fi и оценить |r| (которое определено с помощью уравнения (37)) для каждого возможного выбора fi, θ и qdef. Подставляя в уравнение (39) h, определенный уравнением (38), имеем
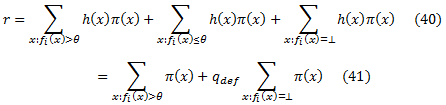
При фиксированном признаке ранжирования fi пусть Xfi = {x∈XΦ | fi(x) ≠ ⊥} будет множеством обратной связи экземпляров, ранжированных по fi. Нам необходимо всего лишь рассмотреть пороговые значения |Xfi| + 1, а именно, {fi(x) | x∈Xfi} ∪ {−∞},так как они определяют все возможные модели поведения экземпляров обратной связи. Кроме того, мы можем непосредственно вычислить первый член уравнения (41) для всех порогов в этом наборе за время O(|Xfi|)просто путем сканирования предварительно отсортированного списка пороговых значений и поддержания частичной суммы очевидным образом.
Для каждого порога, мы также должны оценить |r| для присвоения двух возможных значений qdef (0 или 1). Чтобы сделать это, мы просто должны один раз оценить ∑x:fi(x)=⊥ π(x). Наивно, это занимает O(|XΦ − Xfi|) время, то есть, линейно числу экземпляров без рейтинга. Мы предпочли, чтобы все операции зависели от количества ранжированных экземпляров, так как в таких приложениях, как мета-поиск и поиск информации, каждый признак ранжирования может ранжировать лишь малую часть экземпляров. Чтобы сделать это, обратите внимание, что ∑xπ(x) = 0 по определению π(х). Это означает, что
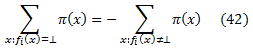
Правую часть этого уравнения можно ясно вычислить за O(|Xfi|)время. Объединяя уравнения (41) и (42), мы получаем
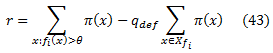
Символический код для слабого обучающегося изображен на рисунке 8. Обратите внимание, что вводные данные алгоритма для каждого признака включают отсортированный список его вероятных порогов {θj}Jj=1. Для удобства будем считать, что θ1 = ∞ и θJ = − ∞. Кроме того, значение |r| рассчитывается по уравнению (43): переменная L накапливает левое слагаемое, а переменная R — правое. Наконец, если значение по умолчанию qdef задается пользователем, то шаг 6 пропускается.
Таким образом, для заданного признака ранжирования общее время, необходимое для оценки |r| для всех вероятных слабых рейтингов, только линейно зависит от количества экземпляров, которые были ранжированы этим признаком. В итоге мы продемонстрировали следующую теорему:
Теорема 5. Алгоритм на рисунке 8 находит слабое ранжирование в виде уравнения (38), которое максимизирует |r|, как в уравнении (39).
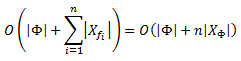
Если обратная связь является двудольной, то время выполнения может быть уточнено до O(n|XΦ|).
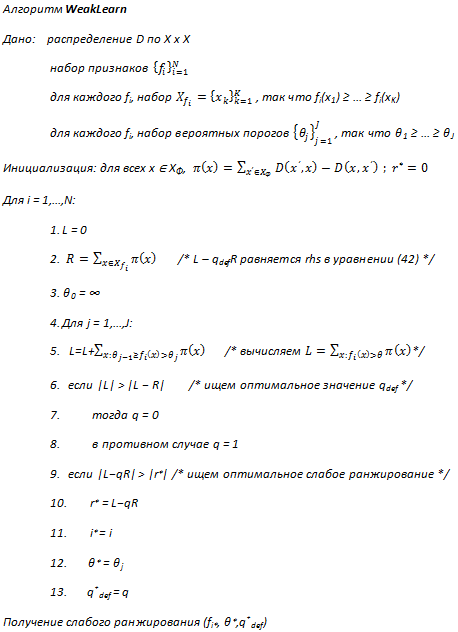
Рисунок 8. Слабый ученик
Положительные суммарные веса. Поскольку окончательное ранжирование имеет вид H(x)=∑Tt=1αtht(x), а окончательные ранжирования по WeakLearn являются бинарными, и если ht(x) = 1, то ht передает вес αt окончательному значению х. В процессе усиления, WeakLearn может выдать различные рейтинги, что соответствуют различным порогам одного и того же признака f. Если мы рассматриваем эти рейтинги в порядке возрастания порога, мы видим, что перенос значения f к окончательному значению x является суммой весов рейтингов, чьи пороги меньше f(x). Для упрощения дела, если предположить, что ht встречается точно один раз среди h1,…,ht, то если веса αt всегда положительные, то перенос значения f монотонно возрастает значению его заданных экземпляров.
Такое поведение переноса значение признака положительно коррелируется с заданным значением, что желательно при некоторых прикладных задачах. В задаче метапоиска, естественно, стратегия поиска f должна переносить больший вес окончательному значению тех экземпляров, которые появляются выше в его отранжированном списке. Иными словами, было бы странно, если, например, f переносил больший вес экземплярам в середине списка и меньший для обоих концов, как было бы в случае, если некоторые из αt были отрицательными. Кроме того, с точки зрения обобщенной погрешности, если мы позволим некоторым αt иметь отрицательное значение, то мы можем построить произвольные функции пространства экземпляра с помощью ограничения одного лишь признака, и это, вероятно, более сложно, чем хотелось бы при сочетании рейтингов (во избежание переобучения). В то время как RankBoost может иметь некоторые αt с отрицательным значением, мы разработали альтернативную версию, которая обуславливает условие того, что все значения αt являются положительными. Таким образом, каждый признак ранжирования должен положительно коррелироваться с окончательным рейтингом, который выдает алгоритм RankBoost.
Для решения этой проблемы, мы реализовали дополнительную версию WeakLearn, что выбирает рейтинги, которые бы обладали монотонным поведением. На практике, наше предположение, что все ht уникальны, может не сохранятся. Если это не так, то взнос конкретного рейтинга h будет равняться его суммарному весу, сумме тех αt, для которых ht = h. Таким образом, мы должны убедиться, что этот суммарный вес является положительным. Наша реализация выводит рейтинг, который максимизирует |r| при ограничении, что суммарный вес этого рейтинга остается положительным. Мы называем этого модифицированного слабого ученика как WeakLearn.cum.
В этом разделе мы выведем границу обобщенной погрешности комбинированного рейтинга, когда слабые рейтинги являются бинарными функциями, а обратная связь двудольная. То есть, мы предполагаем, что обратная связь разбивает пространство экземпляра X на два непересекающихся множества, X и Y, таких, что Φ (х, у)> 0 для всех х ∈ X и y ∈ Y, то есть экземпляры в Y ранжируются выше, чем в X. Многие задачи можно рассматривать как обеспечение двудольной обратной связи, включая задачи метапоиска и рекомендации фильма, а также многие из задач информационного поиска (Salton, 1989, Salton и McGill, 1983).
До этого момента мы не обсуждали, откуда берутся наше обучение и тестовые данные. Обычным условием машинного обучения является то, что существует заданное и неизвестное распределение по пространству экземпляров. Обучающая выборка (и тестовая выборка) представляет собой набор независимых выборок в соответствии с этим распределением. Эта модель явно преобразуется в формулировку классификации, цель которой заключается в прогнозе класса экземпляра. Обучающая выборка состоит из независимой выборки случаев, где каждый экземпляр помеченный правильным классом. Алгоритм обучения формулирует правила классификации после запуска на обучающей выборке, а оценка правила происходит на тестовой выборке, которая является отдельной независимой выборкой немеченых экземпляров.
Эта вероятностная модель не преобразуется легко в ранжированный список, однако, ее целью является прогноз порядка пар экземпляров. Естественный подход для двудольного случая будет предполагать заданное и неизвестное распределение D по X х X, пары из пространства экземпляра (Обратите внимание, что предположение распределения по X х Y упрощает проблему ранжирования: правила, которое всегда ранжирует второй экземпляр над первым, является совершенным).
Очевидно, следующим шагом следует объявить обучающую выборку коллекцией случайно выбранных экземпляров, согласно D. Обобщенные результаты классификации затем тривиально распространяются на ранжирование. Проблема состоит в том, что пары в обучающей выборке не являются независимыми: если (x1,y1) и (x2,y2) находятся в обучающей выборке, то (x1,y2) и (x2,y1) тоже.
Здесь мы представляем модифицированный подход, который позволяет выбирать независимые предположения. Вместо одного распределения D, мы предполагаем существование двух распределений, D0 по X и D1 по Y. Обучающие экземпляры являются объединением независимой выборки в соответствии с D0 и независимой выборки соответствии с D1. (Это похоже на «две кнопки» обучающей модели в классификации, как описано на Haussler и др.. 1991.). Обучающая выборка тогда состоит из всех пар обучающих экземпляров.
Рассмотрим задачу по рекомендации фильма в качестве примера для этой модели. Модель предполагает, что фильмы, просмотренные пользователем, можно разбить на независимую выборку хороших фильмов и независимую выборку плохих фильмов. Это предположение не совсем верное, так как люди обычно выбирают фильмы для просмотра, основываясь на том, какие фильмы они видели. Тем не менее, такие независимые предположения являются общими в области машинного обучения.
Задавая эту вероятностную модель проблемы ранжирования, мы можем теперь определить обобщенную погрешность. Конечное ранжирование по RankBoost имеет вид
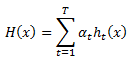
и упорядочивает экземпляры в соответствии с присвоенными значениями. Мы имеем здесь дело с прогнозами таких рейтингов по парам экземпляров, поэтому рассмотрим рейтинги в виде H: X x X → {-1,0,+1}, где
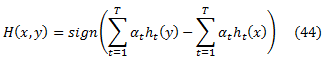
где ht берется из некоторого класса бинарных функций H. Пусть C будет множеством всех таких функций H. Функция H изменяет порядок (x,y) ∈ X x Y, если H(x,y) ≠ 1, что приводит нас к определению обобщенной погрешности Н как
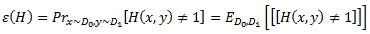
Проверим сначала, что это определение согласуется с нашим понятием ошибки тестирования. Для заданной контрольной выборки T0 x T1, где T0 = ‹x1,…,xp› и T1 = ‹y1,…,yq›, ожидаемая ошибка тестирования H равняется
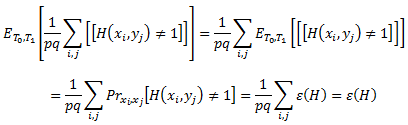
Аналогичным образом, если у нас есть обучающая выборка S0 x S1, где S0 = ‹x1,…,xm› и S1 = ‹y1,…,yn›, обучающая (или эмпирическая) погрешность Н равняется
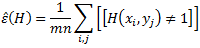
Наша цель заключается в том, чтобы показать, что, с большой долей вероятности, разница между εˆ(H) и ε(H) мала, а это означает, что производительность комбинированного рейтинга H на обучающей выборке будет такой же и на любой случайной выборке.
Теперь мы ограничиваем разницу между обучающей и тестированной погрешностями комбинированного рейтинга, полученного алгоритмом RankBoost с использованием стандартных методов анализа VC-размерности (Devroye соавт., 1996, Vapnik, 1982). Покажем, что, если обучающая выборка выбирается с большой долей вероятности, то эта разница мала для каждого H ∈ C. Если это произойдет, то независимо от того, какой комбинированный рейтинг выбирается нашим алгоритмом, обучающая погрешность комбинированного рейтинга точно оценит его обобщающую погрешность. Другой способ решения этой проблемы заключается в следующем. Пусть Z означает событие, когда существует такое H ∈ C, что εˆ(H) и ε (H) отличаются более чем на узко указанный интервал. Тогда вероятность (выбора обучающей выборки) из событий Z очень мала. Формально, мы покажем, что для каждого δ > 0, существует небольшоеε такое, что
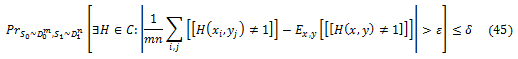
где выбор ε будет определен в ходе доказательства. Наш подход будет разделять уравнение (45) на две вероятности: одну для выбора S0, а другую для выбора S1, а затем ограничит каждую из них, используя теоремы классификации обобщенной погрешности. Для того чтобы использовать эти теоремы, нам нужно будет превратить H в бинарную функцию. Определить F: X x Y → {0,1} как функцию, которая показывает, изменяет ли H порядок пар (x,y), что означает, что F(x,y) = [[H(x,y) ≠1]]. Хотя H является функцией на X x X, мы заботимся только о том, как она работает на парах (x,y) ∈ X х Y, что означает, что она не имеет ошибки упорядочения двух экземпляров из X или Y. Величину внутри абсолютного значения уравнения (45) можно записать в виде
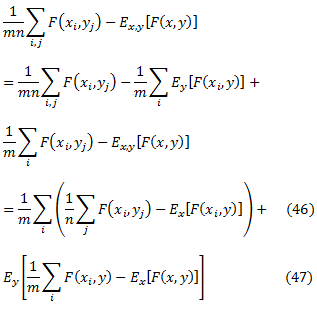
Так что, если мы докажем, что существуют такие ε0 и ε1, что ε0 +ε1 = ε и
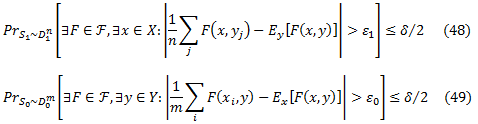
мы покажем с большой долей вероятности в уравнении (45), что слагаемое уравнения (47) будет меньше, чем ε1 для каждого xi, откуда следует, что среднее значение будет меньше, чем ε1. Кроме того, величина внутри ожидании уравнения (47) будет меньше, чем ε0 для каждого у и так ожидание будет меньше, чем ε0. Докажем уравнение (49) с использованием результатов стандартной классификации и уравнение (48), следуя аргументу симметрии. Рассмотрим уравнение (49) для фиксированного у, это означает, что F(x,y) является единственным аргументом бинарной функции. Пусть Fy будет множеством всех таких функций F при фиксированном у. Тогда выбор F в уравнении (49) возникает от UyFy. Теорема Вапника (1982) относится к уравнению (49) и дает выбор ε0, которая зависит от размера m обучающего множества S0, вероятности ошибки δ и сложности d’UyFy, и измеряется как VC-размерность (см. подробнее Vapnik 1982 или Devroye соавт., 1996). В частности, для любого δ > 0,
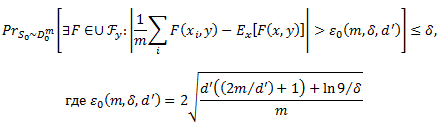
Заданы параметры m и δ; осталось вычислить d’, VC-размерность для UyFy. (Заметим, что хотя мы используем результат классификации для ограничения уравнения (49), вероятность соответствует своеобразной задаче классификации (пытаясь отличить X от Y, выбирая F и один у ∈ Y), что, кажется, не имеют естественной интерпретации). Определим вид функций в UyFy. Для заданного y ∈ Y,
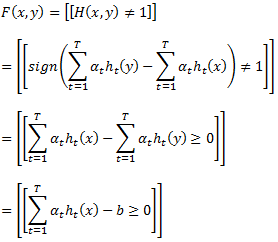
где b=∑Tt=1αtht(y) является константой, потому что у фиксировано. Таким образом, функции в UyFy представляют собой подмножество всех возможных порогов всех линейных комбинаций слабых рейтингов T. Теорема 8, предложенная Freud и Schapire (1997), ограничивает VC-размерность этого класса относительно T и VC-размерности класса слабого рейтинга H. Применяя их результат, мы получаем, что если H имеет VC-размерность d ≥ 2, то d’ по большей мере
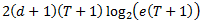
где e — основание натурального логарифма. На последнем шаге, повторяя те же обоснования для уравнения (48), поддерживая х фиксированным, и собирая все вместе, мы доказали, основной вывод данного раздела:
Теорема 8. Пусть С будет множеством всех функций вида, данного в уравнении (44), где все ht принадлежат к классу H VC-размерности d. Пусть S0 и S1 будут выборками размера m и n соответственно. Тогда с вероятностью выбора обучающей выборки не менее 1 — δ, все H ∈ C удовлетворяют
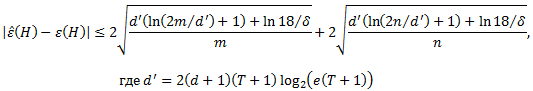
Обучение ранжированию I. Попарный подход. Часть 1: Ranking SVM
Обучение ранжированию I. Попарный подход. Часть 3: Экспериментальная оценка RankBoost
Оригинал: «An Efficient Boosting Algorithm for Combining Preferences»
Ссылки:
Brian T. Bartell, Garrison W. Cottrell, and Richard K. Belew. Automatic combination of multiple ranked retrieval systems. In Proceedings of the 17th Annual International ACM SIGIR Conference on Research and Development in Information Retrieval, 1994.
Peter L. Bartlett. The sample complexity of pattern classification with neural networks: the size of the weights is more important than the size of the network. IEEE Transactions on Information Theory, 44(2):525–536, March 1998.
Rich Caruana, Shumeet Baluja, and Tom Mitchell. Using the future to “sort out” the present: Rankprop and multitask learning for medical risk evaluation. In Advances in Neural Information Processing Systems 8, pages 959–965, 1996.
William W. Cohen, Robert E. Schapire, and Yoram Singer. Learning to order things. Journal of Artificial Intelligence Research, 10:243–270, 1999.
Michael Collins. Discriminative reranking for natural language parsing. In Proceedings of the Seventeenth International Conference on Machine Learning, 2000.
Luc Devroye, Lazlo Gyorfi, and Gabor Lugosi. A Probabilistic Theory of Pattern Recognition. Springer, 1996.
O. Etzioni, S. Hanks, T. Jiang, R. M. Karp, O. Madani, and O. Waarts. Efficient information gathering on the internet. In 37th Annual Symposium on Foundations of Computer Science, 1996.
Yoav Freund and Robert E. Schapire. A decision-theoretic generalization of on-line learning and an application to boosting. Journal of Computer and System Sciences, 55(1):119–139, August 1997.
David Haussler. Decision theoretic generalizations of the PAC model for neural net and other learning applications. Information and Computation, 100(1):78–150, 1992.
David Haussler, Michael Kearns, Nick Littlestone, and Manfred K.Warmuth. Equivalence of models for polynomial learnability. Information and Computation, 95(2):129–161, December 1991.
Will Hill, Larry Stead, Mark Rosenstein, and George Furnas. Recommending and evaluating choices in a virtual community of use. In Human Factors in Computing Systems CHI’95 Conference Proceedings, pages 194–201, 1995.
Raj D. Iyer, David D. Lewis, Robert E. Schapire, Yoram Singer, and Amit Singhal. Boosting for document routing. In Proceedings of the Ninth International Conference on Information and Knowledge Management, 2000.
Paul Resnick, Neophytos Iacovou, Mitesh Sushak, Peter Bergstrom, and John Riedl. Grouplens: An open architecture for collaborative filtering of netnews. In Proceedings of Computer Supported Cooperative Work, 1995.
Gerard Salton. Automatic text processing: the transformation, analysis and retrieval of information by computer. Addison-Wesley, 1989.
Gerard Salton and Michael J. McGill. Introduction to Modern Information Retrieval. McGraw-Hill, 1983.
Robert E. Schapire, Yoav Freund, Peter Bartlett, and Wee Sun Lee. Boosting the margin: A new explanation for the effectiveness of voting methods. The Annals of Statistics, 26(5):1651–1686, October 1998.
Robert E. Schapire and Yoram Singer. Improved boosting algorithms using confidence-rated predictions. Machine Learning, 37(3):297–336, December 1999.
Upendra Shardanand and Pattie Maes. Social information filtering: Algorithms for automating “word of mouth”. In Human Factors in Computing Systems CHI’95 Conference Proceedings, 1995.
V. N. Vapnik. Estimation of Dependences Based on Empirical Data. Springer-Verlag, 1982.
Marilyn A. Walker, Owen Rambow, and Monica Rogati. SPoT: A trainable sentence planner. In Proceedings of the 2nd Annual Meeting of the North American Chapter of the Associataion for Computational Linguistics, 2001.
Полезная информация по продвижению сайтов:
Перейти ко всей информации