SEO-Константа
Яндекс.Директ + оптимизация
Теперь, когда мы окончательно разобрались с оценками, давайте попытаемся подобрать наиболее оптимальную функцию доверия, сообразно логике следования от простого к сложному. В дальнейшем, собрав воедино все полученные данные, мы сможем построить сам алгоритм доверия TrustRank. Учитывая ограниченность наших с вами попыток L на вызов функции прогнозирования O (причины были указаны нами ранее), мы будем избирательно подходить к ее вызову для всех случайных документов из имеющейся выборки S (далее мы познакомим вас с методикой создания наиболее оптимальной выборки). После получения необходимых прогнозов, нашей задачей является мануальная пометка выявленного вероятностного набора плохих (S-) и хороших (S+) интернет-страниц, а также учет того, что оставшаяся часть непроверенных нашими экспертами документов в коллекции будет иметь показатель доверия равный 1/2. Как вы наверно уже поняли, основной причиной столь значительного урезания доверия к ним является недостаток имеющейся у нас информации об их содержимом. По причине нехватки знаний о подобного рода страницах, мы вводим в рассмотрение, так называемую, функцию условного доверия Τ0, определенную для любого Р ⊂ V следующим образом:
Функция условного доверия

Например, мы можем ограничить количество наших попыток L на вызов функции прогнозирования до 3-х и использовать сей метод применительно к тому ориентированному графу, который был изображен на нашем с вами Рис. 2 в предыдущей части данного материала. Следовательно, в случайным образом исследуемой выборке S = {A, C, F}, а векторами прогнозирования и условного доверия для каждой анализируемой страницы будут являться O и Τ0:
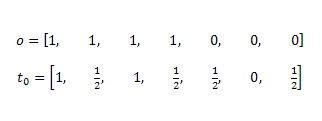
Для того чтобы мы могли оценить производительность функции условного доверия Τ0 давайте сделаем предположение, что в этой выборке χ имеются все наши 7 интернет-страничек (от A до G) из Рис. 2 и мы можем отсортировать все возможные 42 пары (7*6=42) по одному запросу. Тогда для функции условного доверия показатель попарного ранжирования составляет 17/21, пороговое значения δ будет равно 1/2, метрика точности и полноты составит 1 и 1/2 соответственно.
Распространение доверия
Воспользуемся аппроксимацией отчуждения хороших веб-документов от плохих. Для вызова функции прогнозирования доверия O, мы по прежнему будем выбирать документы из имеющейся выборки S случайным образом и, если в результате наших вызовов окажется, что хорошие документы вероятней всего ссылаются на точно такие же качественные источники информации (то есть, имеем связанный набор S+), мы присваиваем показатель доверия равным 1 всем страницам в пределах Μ -го перехода (шага) по ссылкам от одной вершины к другой. Соответственно:
Функция пошагового доверия

,где q → Μ p указывает на наличие максимально длинного пути Μ между страницами q и p, в достижимости которых исключается существование плохих документов. Сейчас мы опять вернемся к нашему замечательному Рисунку 2, а также к выборке S = {A, C, F}, и попытаемся рассчитать показатель траста для трех различных значений функции пошагового доверия:
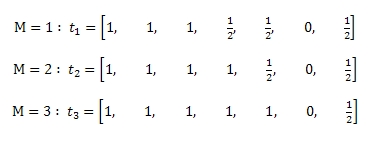
| M | pairord | prec | rec |
| 1 | 19 / 21 | 1 | 3 / 4 |
| 2 | 1 | 1 | 1 |
| 3 | 17 / 21 | 4 / 5 | 1 |
Мы ожидаем, что в отношении ряда метрик функция пошагового доверия покажет более точные результаты, нежели чем функция условного доверия. Действительно, в Таблице 1 наглядно продемонстрировано, что при Μ =1 и Μ =2, как попарное ранжирование, так и точность-полнота имеют показатели равные 1. Мы также можем засвидетельствовать, что по причине цитирования плохого документа E качественной страничкой D (данная дуга была помечена на нашем ориентированном графе звездочкой) при переходе к Μ =3 наблюдается снижение производительности функции доверия.
Единственное, что может вызывать у нас сомнения в плане эффективной применимости данного метода в сети заключается в том, что мы не можем со стопроцентной уверенностью утверждать факт наличия полностью идентичных по всем своим положительным свойствам страниц в существующей достижимости между хорошими вершинами q и p. На самом деле, чем более мы удаляемся от центра кластера хороших интернет-ресурсов, тем меньше наша уверенность в том, что каждый последующий процитированный сайт окажется хорошим. Если мы еще раз посмотрим на Рис. 2, то можно обнаружить примерно следующее: вероятность того, что мы останемся в пределах отмеченного набора S+ в два шага (пройдя по ссылке от документа A к странице B, а затем до документа D) составляет 1. Если же рассматривать три шага, то мы тотчас попадаем на третью вершину нашего ориентированного графа F, который является уже некачественным документом, поэтому вероятность выхода на хорошую HTML-страничку в этом случае снижается до 2/3.
Затухание доверия
Поскольку описанная выше ситуация демонстрирует нам затухание доверия по мере отдаления от центра кластера качественных веб-сайтов, мы постараемся описать несколько возможных методик для учета данного фактора. Первая из них может быть проиллюстрирована с помощью следующего рисунка:
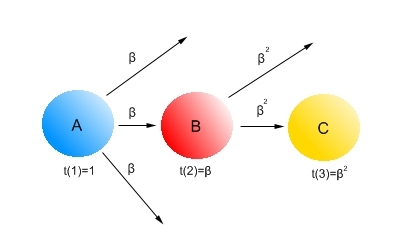
Рис. 3 Амортизация доверия
В наших расчетах мы будем учитываем не только качественную составляющую ссылок между страницами, но и их количественную сторону. Поэтому, если иметь в виду, что страницу B единожды процитировал качественный документ A, то нам следует присвоить данной связи и непосредственно веб-странице В значение затухания доверия равное β, где β < 1. Тогда, при втором переходе (шаге) по одиночному линку с документа B на страницу C показатель доверия составит β · β. В том же случае, если имеется несколько входящих ссылок на документ (например, за веб-страницу C проголосовал не только документ B, но и A), мы бы могли использовать первоначальное максимальное (было бы β) или усредненное значение доверия β, последнее в нашей схеме рассчитывалось бы как (β + β · β) / 2.
Для того, чтобы объяснить вам следующую методику учета затухающего доверия при каждом последующем переходе по ссылкам от одного документа к другому, обратимся к такому примеру из социальных сетей, как наличие у того или иного аккаунта определенного количества друзей. Логично предположить, что вероятность того, что мы встретим спамера при малом количестве друзей является достаточно незначительной, поскольку наш с вами аккаунт знаком с каждым из имеющегося у него в друзьях человеком и может за него поручиться. Однако, если у него будет очень много виртуальных друзей, то возможность появления в общем списке спамера существенно возрастает. Точно такую же картину мы можем наблюдать и в области проставления каким-либо сайтом ссылок на сторонние ресурсы. Если исходящих линков не так уж и много, то можно предположить, что владелец сайта тщательно выбирает соседей по сети, а, следовательно, есть вероятность того, что все они окажутся хорошими web-ресурсами. Эмпирические данные показывают, что сайты, содержащие большое количество исходящих ссылок (тщательность проверки цитируемых сайтов обратно пропорциональна их количеству), чаще других участвуют в передаче голосующей способности некачественным документам. Все это наводит на мысль о дроблении доверия в зависимости от распределения голосующей способности сайта между прочими ресурсами сети. Таким образом, если наш с вами документ p имеет показатель доверия Τ (p) и ссылается на какое-то число внешних страниц ω (p), то «голос» нашего доверия будет распределяется между всеми исходящими ссылками Τ(p)/ ω(p). В этом случае, реальное доверие ко всякой web-странице будет складываться из суммы дробных оценок голосующих за нее веб-ресурсов. Продолжая начатое логическое рассуждение можно придти к такому выводу, что накопленый показатель доверия (чем больше на нас ссылаются хороших сайтов или, при меньшем их количестве, каждый из них скупиться передавать свою голосующую способность, тем качественней будет осуществляться продвижение сайта) является для нас весомым аргументом для того, чтобы считать документ качественным. Суммирование дробных оценок будет осуществляться в стандартном диапазоне [0,1].
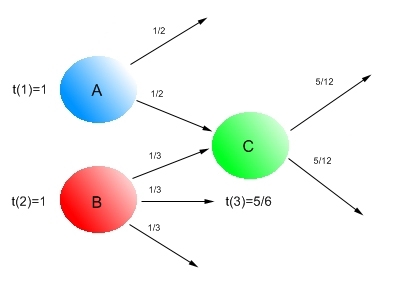
Рис. 4 Дробление (сплиттинг) доверия
Как вы можете видеть, Рис. 4 демонстрирует нам процесс дробления доверия между цитируемыми web-страницами. Поскольку страница A из набора S+ имеет два исходящих линка, то, соответственно, показатель доверия делится между этими ссылками пополам и документ C в этом случае получает только 1/2 необходимого ему доверия. Аналогично, документ B имеет уже три исходящие ссылки, поэтому каждая из них отдаст во внешнюю интернет-среду по 1/3 доверия. После всех произведенных подсчетов, наша HTML- страничка C в общей сложности накапливает 5/6 доверия (1/2+1/3=5/6). Помимо этого, мы также можем объединить процесс сплиттинга с амортизацией, тогда документ C будет иметь показатель доверия равный β · (1/2+1/3).

На Рис. 5 показана последовательность выполнения алгоритма доверия: на вход поступает ориентированный граф (матрица переходов, количество веб-страниц) и контролирующие данный процесс параметры (ограничение на вызов функции прогнозирования, коэффициент затухания, число итераций), а на выходе мы получаем значение TrustRank. В качестве первого шага алгоритм вызывает функцию SelectSeed, возвращающую вектор s. Это позволяет определить и сформировать набор наиболее предпочтительные страниц p для последующего анализа всех прочих документов. Более подробно функцию SelectSeed мы рассмотрим несколько позже, однако на данном этапе применимо к нашему с вами Рисунку 2 функция SelectSeed вернет следующий вектор:

На втором шаге функция Rank(x,s) осуществляет перестановку х’ вектора х, с элементами x’(i) в порядке убывающей s(x’(i)). Проще говоря, выполняется ранжирование элементов х в порядке убывающего значения вектора s. В нашем примере это будет выглядеть следующим образом:
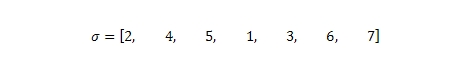
Определив наилучший по всем своим характеристикам интернет-документ (в нашей выборке им может считаться страница B, далее следует D и пр.), программа переходит к третьему шагу. Здесь для данного множества предпочтительных документов, определенного еще на первом этапе работы алгоритма, вызывается функция прогнозирования доверия. Тем элементам статистического распределения вектора d, которые соответствуют качественным HTML-страничкам, присваивается показатель доверия равный единице. Четвертый шаг нормализует статистическое распределение вектора d таким образом, чтобы в сумме его элементы давали бы нам 1. Предположим, что ограничение на вызов функции прогнозирования L составляет 3 раза, выборка тоже состоит из 3-х цифровых документов {B, D,E}. Тогда, если страницы B и D являются по всем своим характеристикам качественными ресурсами, мы получаем следующее статистическое распределение вектора:
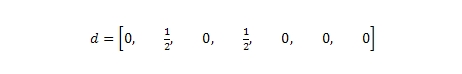
В завершении процесса, мы получаем значение TrustRank, сама математическая модель подсчета которого по сути является одной из модификаций алгоритма авторитетности PageRank. Обратите внимание, что при каждой осуществляемой итерации Mβ нашего алгоритма, во-первых, доверие к тому или иному узлу расщеплялось между всеми его соседями по сети (то есть, осуществлялся его сплиттинг), а во-вторых, учитывался коэффициент затухания αβ. Предположим, что он у нас составляет общепринятые 0.85, количество итераций алгоритма 20, тогда имеем:

Несмотря на тот факт, что после всех наших итераций показатели доверия наших страничек B и D заметно снизились, их значения все еще остаются достаточно высокими. Интересно также еще и то, что более низкое доверие к странице D по сравнению с документом B было обеспечено за счет того, что за последний проголосовала авторитетная страница C. Таким образом, алгоритм TrustRank по сути лишний раз подтверждает и, более того закрепляет, гипотезы, данные функции прогнозирования. При желании мы можем нормализовать итоговый вектор посредством деления всех полученных оценок на максимальное значение доверия (прировняв доверие страницы B к единице), но такая операция нисколько не повлияет на порядок документов и, соответственно, наши выводы. В любом случае, наибольшее доверие будет присвоено хорошим страницам (B,C,D), а плохие документы (F,G) будут иметь низкий бал. Однако нам не удалось дать адекватную оценку A и E страницам, поскольку для документа A в нашей модели не нашлось входящей ссылки и ей просто не откуда было накапливать свое доверие (0) — следовательно даже хороший документ без входящих ссылок получает априори заниженный бал. Плохая страница E, как ни странно это может прозвучать, получила завышенную оценку, поскольку на нее ссылается хороший документ D. Тем не менее, несмотря на подобного рода погрешности, в реально функционирующей интернет среде алгоритм TrustRank эффективно идентифицирует хорошие сайты от некачественных ресурсов, поэтому нам стоит полагаться на ту информацию, которую он сообщает разработчикам поисковых систем.
Как вы наверно помните, основная цель рассмотренной выше функции SelectSeed заключалась в поиске и формировании набора своего рода эталонных, предпочтительных веб-документов, которые помогли бы нам отыскать прочие хорошие страницы на основании присущих качественным документам характеристикам. Вместе с тем, мы также говорили о том, что у нас имеется очень жесткие ресурсные ограничения на количество вызовов функции прогнозирования, поэтому исследуемые набор предпочтительных страниц для ее вызова должен быть исключительно минимальным. Сейчас, помимо формирования набора для функции SelectSeed из случайных страниц мы рассмотрим еще несколько стратегий определения эталонов, которые основываются на показателе PageRank.
Инверсивный (обратный) PageRank
Как вы понимаете, основным источником доверия для любого сайта в сети будет являться входящая ссылка с какого-нибудь авторитетного ресурса, например, каталога DMOZ. Поэтому, если мы будем рассматривать вопрос передачи доверия в контексте наших с вами экспериментов (то есть, «от одного к множеству») и еще раз возвратимся к упрощенной модели ориентированного графа (Рис. 2) с набором хороших и плохих страниц, то для формирования выборки мы можем отдавать предпочтение тому авторитетному документу, который имеет множество исходящих ссылок на прочие web-странички. Теперь выберем из нашей выборки документы с наибольшим количеством исходящих ссылок B и E (то есть, S = {B, E} ) и установим ограничение на вызов функции прогнозирования L = 2. Если продолжить логику наших рассуждений, касательно данного метода, то можно придти к его гипотетической возможности осуществить вершинное покрытие, поскольку мы также можем учитывать те страницы, которые были процитированы этими двумя HTML-страничками, (то есть, выполняется условие, что каждое ребро инцидентно минимум одной вершине графа), и так далее. Все это приводит нас к модели, тесно связанной с алгоритмом PageRank, за тем исключением, что здесь речь идет не о входящих, передающих голоса ссылках, а об исходящих, отдающих свой авторитет. Именно по этой причине мы и называем данную схему обратным PR. Соответственно, для того, чтобы выявить значимость web-документа нам следуют выполнить расчет PageRank на нашем ориентированном графе ζ = (υ, ε ), где:

Рис. 6 Алгоритм обратного PageRank
Важно иметь ввиду, что в приведенном на Рисунке 6 алгоритме инверсивного PageRank мы, во-первых, используем не прямую, а обратную матрицу переходов, что несколько отличает текущий подсчет от классического подхода, а во-вторых, количество совершаемых итераций (ΜΙ = 20) и коэффициент затухания (αΙ = 0.85) могут отличаться от тех значений, которые мы использовали в алгоритме TrustRank. Поэтому для нашего Рисунка 2, показатель обратного PR будет давать следующие значения:

Теперь для новой выборки S = {B, D, E} установим ограничение на вызов функции прогнозирования L=3, но так как мы изначально знаем, что наибольшее количество исходящих ссылок имеют документы B и D, то используем их в качестве отправной точки и на этот раз. Отметим, что обратный PageRank не имеет четкого математического обоснования, но в то же время является эвристическим алгоритмом (их еще иногда называют эвристиками), то есть таким алгоритмом, который базируется на соображениях интуиции. Например, нам кажется, что подобная эвристика приведет к нас наиболее оптимальному решению, однако это может оказаться и ошибочным суждением. Безусловным плюсом эвристиков является то, что они быстро и/иногда часто работают, да и в целом применимы на практике. Именно по этой самой причине в решении подавляющего большинства практических задач наш обратный PageRank покажет превосходные результаты о чем мы вам впоследствии также подробно расскажем. В чем же выражается его эвристика более конкретно? Во-первых, он и не гарантирует нам максимальное покрытие вершин.
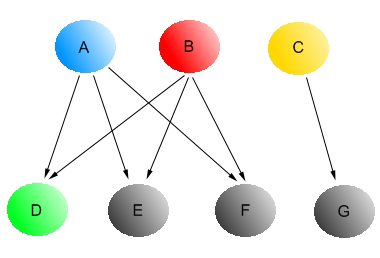
Рис. 7 Обратный PageRank в задаче максимального вершинного покрытия
Допустим, если мы обратимся к Рисунку 7 и установим ограничение на вызов функции прогнозирования L=2, то, максимальное вершинное покрытие реализуется за счет множества страниц {A, C} или {B, C}. Однако обратный расчет PR дает следующее значение вектора:
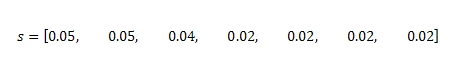
что приводит нас к выборке {A, B}. Невзирая на все это, обратный PageRank остается для нас очень полезным инструментом, поскольку время, которое мы потратим на выполнения поставленных перед нашим алгоритмом задач, будет зависеть в некоторой степени от их сложности. Говоря иными словами, оно полиноминально и частично увязано с количеством исследуемых страниц. В то время, как определение максимального вершинного покрытия является классическим примером NP-полной задачей, то есть такой задачи, для решения которой не найдены полиноминальные алгоритмы, но сей факт еще не дает нам права отрицать их существование вообще. Задача максимального вершинного покрытия сходна с задачей независимого множества вершин на ориентированном [1] графе. Стоит упомянуть, что независимым множеством называется произвольно избранное множество попарно не смежных, изолированных вершин графа, а суть данной задачи сводится к поиску наибольшего и/или максимального независимого множества. В случае использования для ее решения той же элементарной эвристики, мы приходим к созданию, так называемого, жадного алгоритма, который работает за полиноминальное время. Несмотря на свое оптимальное пошаговое исполнение, в конечном счете, такой полиноминальный алгоритм не может гарантировать нам оптимальное решение задачи, относящейся к упомянутому классу NP-полных.
Вторая причина, по которой мы можем отнести обратный PageRank к эвристическому подходу заключается в том, что поиск максимального вершинного покрытия является далеко не самой выгодной для нас стратегией и для того чтобы вам это доказать нам необходимо распространить доверие посредством вышеупомянутого расщепления (сплиттинга), игнорируя его затухание. Если мы вернемся к Рисунку 7 и попытаемся сравнить то доверие, которое передается документами B и C цитируемым web-страничкам, то окажется, что в первом случае страница B отдала D,E и F по 1/3 доверия, а документ C отдает странице G единицу. Соответственно, при втором варианте с меньшим покрытием, мы будем более уверены в качестве исследуемых страниц. Тем не менее, вопрос о предпочтении меньшего или большего (получить большее количество данных в ущерб их точности) покрытия должен зависеть от каждой конкретной ситуации и остаться в рамках текущей работы открытым.
Страницы с высоким PageRank
До сих пор мы предполагали, что оценка авторитетности того или иного веб-документа никак не скажется на его качестве. Однако, как мы с вами понимаем, та страничка, за которую проголосовали ее соседки по сети, должна занимать более высокие позиции (речь, естественно, идет о предоставлении пользователю документа, релевантного его поисковому запросу) в органическом поиске тех поисковых систем, которые используют такой алгоритм элементарнейшего статистического учета, как Google PageRank. Давайте попытаемся предложить формальное доказательство того, что HTML-страница с высоким значением PageRank имеет большую вероятность оказаться хорошей. Допустим, у нас есть релевантные какому-то запросу документы p, q, r и s. Упорядочивание же этих страниц в результатах выдачи будет осуществляться в порядке их убывающего PR: на первом месте окажется документ p, затем — q и т.д. Представим себе такую ситуацию, что пользователь нашел ответ на свой вопрос в содержимом страниц p и q, а r и s не были им рассмотрены и/или даже просмотрены, но на следующей странице результатов поиска. Как вы полагаете, есть ли рациональное зерно в том утверждении, что первые две страницы являются и в нашем случае более полезными для определения выборки хороших документов? Верна ли наша догадка о том, что авторитетная страница с высоким Google PR, если и будет на кого-то ссылаться, то, скорее всего, это будет не менее качественный веб-документ? Думаем, что да, и наш эвристический подход к подборке страниц для SelectSeed должен учитывать показатель PageRank. Хотя, стоит заметить, при выборе страниц на основании высокого PR (данные будут очень точными), мы получим куда меньшую выборку нежели чем при учете инверсионного показателя авторитетности.
Страница материала:
Детекция поискового спама. Часть 1: Введение в алгоритм Google TrustRank
Детекция поискового спама. Часть 2: Расчет алгоритма Google TrustRank
Детекция поискового спама. Часть 3: От TrustRank к алгоритмам HostRank и DirRank
Детекция поискового спама. Часть 4: HostRank или PageRank, вычисляемый по графу хостов
Детекция поискового спама. Часть 5: От DirRank к алгоритму Truncated PageRank
Детекция поискового спама. Часть 6: Truncated PageRank и Вероятностный Подсчет
Детекция поискового спама. Часть 7: Знакомство с алгоритмом BadRank, обнуляющим Google PageRank
Детекция поискового спама. Часть 8: Google BadRank и ParentPenalty
Детекция поискового спама. Часть 9. Введение в алгоритм SpamRank
Детекция поискового спама. Часть 10: От исследования SpamRank к алгоритму Anti-TrustRank
Детекция поискового спама. Часть 11: Эксперименты с алгоритмом недоверия Anti-TrustRank
Детекция поискового спама. Часть 12: Применение принципов термодиффузионной
Детекция поискового спама. Часть 13: Детальный анализ алгоритма ранжирования DiffusionRank
Детекция поискового спама. Часть 14: Вычисление AIR на веб-графе, эквивалентного электронной схеме
Детекция поискового спама. Часть 15: Применение искусственных нейронных сетей
Полезная информация по продвижению сайтов:
Перейти ко всей информации