Поведенческие факторы. Часть 1: Введение в алгоритм BrowseRank

В первой части нашего с вами материала, посвященного поведенческим факторам ранжирования, мы поговорим о новом способе оценки важности веб-страниц, который называется BrowseRank. Традиционный подход к расчёту важности использует ссылочную структуру Сети и строит модель, основанную на веб-графе. Например, PageRank – алгоритм, использующий дискретно-временной процесс Маркова в качестве модели для работы. К сожалению, ссылочный граф может быть неполным и неточным в рамках определения важности веб-страницы, так как ссылки могут быть легко добавлены и удалены веб-мастерами. Далее предлагается рассчитывать важность страниц с помощью графа сёрфинга пользователя, созданный на основе данных о поведении пользователя. В этом графе вершинами являются сами страницы, а ориентированными рёбрами – переходы по страницам в истории пользователя. Кроме того, принимается во внимание время, проведённое пользователем на странице. Граф сёрфинга пользователя более надёжен в определении важности веб-страниц по сравнению с ссылочным графом. Ниже предлагается применение непрерывно-временного процесса Маркова к графу сёрфинга пользователя в качестве модели для работы и расчёт стационарного распределения вероятностей процесса в виде важности веб-страницы. Так же был разработан эффективный алгоритм необходимых вычислений. Таким образом, появляется возможность учитывать неявное голосование сотен миллионов пользователей за важность той или иной веб-страницы. Результаты экспериментов показывают, что BrowseRank в действительности качественно превосходит такие алгоритмы PageRank и TrustRank в ряде задач.

Введение в алгоритм BrowseRank

Важность страницы, отражающая её «вес» в Сети, является ключевым фактором в веб-поиске, так как в современных поисковых машинах процессы краулинга, индексирования и ранжирования работают на данной метрике. Из-за огромного масштаба и постоянной эволюции Сети точная оценка веса веб-страниц становится критически важной и представляет собой серьёзную задачу для поисковых систем. В текущей работе мы предлагаем новое решение этой задачи. На данный момент важность веб-страниц рассчитывается при использовании ссылочного графа Сети и процесса анализа ссылок. Широко известны такие алгоритмы ссылочного анализа как HITS [15] и PageRank [5,18] (прочие [4, 8, 9, 11, 12, 16, 17, 20]). Большинство алгоритмов предполагают, что если много важных страниц ссылаются на страницу в графе, то последняя также важна с высокой вероятностью. Тогда важность страницы рассчитывается на основе модели, заданной в ссылочном графе. Сегодня алгоритмы ссылочного анализа успешно применяются в веб-поиске. К примеру, PageRank применяет дискретно-временной процесс Маркова к ссылочному графу Сети для расчёта важности страниц, что, фактически, имитирует процесс случайного блуждания (сёрфинга) пользователя по гиперссылкам в Интернете. Несмотря на свои очевидные преимущества, PageRank обладает рядом недостатков.

• Ссылочный граф, на который опирается PageRank, недостаточно надёжен, так как ссылки можно добавлять и удалять по желанию. Например, целенаправленное создание большого количества гиперссылок является излюбленной техникой спамеров (см. линкофермы и обмен ссылками). Такие ссылки, естественно, не подходят для расчёта важности веб-страниц.
• PageRank моделирует процесс случайного блуждания по ссылочному графу, но не берёт в расчёт время, которое пользователь проводит на веб-страницах во время сёрфинга. Однако эта информации может быть хорошим показателем качества и, следовательно, важности веб-страницы.

Для решения этих проблем мы предлагаем использование более надёжного источника информации и применение более мощной математической модели. Сразу же встаёт вопрос – какой источник информации лучше ссылочного графа? Предлагается использование графа сёрфинга пользователя, сгенерированного из данных о поведении пользователя. Следует заметить, что для расчёта важности веб-страниц можно совмещать ссылочный граф и данные о поведении пользователя, но в данной работе это совмещение не рассматривается. Информация о поведении пользователя может быть записана расширениями в интернет-браузерах (например, тулбары Google, Yandex и Yahoo!) и отправлена на сервер. Пример показан на рисунке 1.

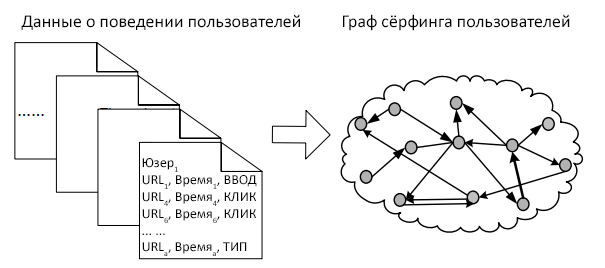
Каждая запись в данных содержит информацию о визитах анонимного пользователя: URL, время на странице, вид перехода (ввод ссылки в адресную строку или клик по ссылке на предыдущей странице). В нашем эксперименте подобные данные были легально записаны и собраны с очень большой группы пользователей с их согласия. Персональные данные, с помощью которых можно установить личность пользователей, не были включены в эксперимент. Используя данные сотен миллионов пользователей возможно построить граф сёрфинга пользователей, в котором вершинами являются веб-страницы, а ориентированными рёбрами – реальные переходы между веб-страницами самими пользователями и длительность посещения. Граф сёрфинга пользователя может более точно отражать процесс случайного блуждания и, следовательно, повысить точность расчёта важности веб-страниц. Чем больше посещений страницы и чем дольше пользователи на ней оставались, тем более вероятно, что страница имеет высокую важность. При помощи данного графа мы можем оценить неявное голосование за важность веб-страницы сотнями миллионов пользователей.

Другим вопросом является выбор алгоритма для обработки новых данных. Очевидно, что использование дискретно-временного процесса Маркова не будет достаточным. В настоящей работе мы используем непрерывно-временной процесс Маркова [23] в качестве модели для графа сёрфинга пользователей. Если считать процесс однородным по времени (что резонно, см. раздел BrowseRank), то стационарное распределение вероятностей может быть использовано для оценки важности веб-страниц. Мы используем алгоритм, называемый BrowseRank для эффективного расчёта стационарного распределения вероятностей в непрерывно-временном процессе Маркова. Так же используется аддитивная (добавочная) шумовая модель (additive noise model) для независимой последовательной оценки параметров в процессе Маркова. Кроме того, мы применяем технологию цепи Маркова (последовательности случайных событий с конечным числом исходов, где при фиксированном настоящем будущее не зависит от прошлого) для ускорения расчёта стационарного распределения. Далее по тексту мы будем называть и алгоритм и выходное значение алгоритма одинаково – BrowseRank.

Результаты экспериментов показывают, что BrowseRank способен достичь более высокой производительности по сравнению с существующими методами оценки, включая PageRank и TrustRank [8], в задачах поиска и ранжирования интернет-страниц; детекции поискового спама; объективной оценки тех ранговых показателей ресурса, которые завышаются коммерческими организациями в том случае, если их интересует продвижение сайтов в органической выдаче. Инновация нашего подхода заключается в следующих утверждениях. Во-первых, мы предлагаем использование графа сёрфинга пользователей, созданного с учётом поведенческих факторов, для расчёта важности веб-страницы, что само по себе надёжнее веб-графа. Во-вторых, мы предлагаем использовать непрерывно-временной процесс Маркова для моделирования случайного блуждания по графу сёрфинга, что более точно отразит важность веб-страниц. И, наконец, в-третьих, нами предлагается алгоритм BrowseRank для эффективного расчёта оценок важности веб-страниц.

PageRank [5, 18] и HITS [15] являются популярными алгоритмами ссылочного анализа. Главная идея PageRank такова: ссылка с одной страницы на другую является поддержкой (одобрением) последней. Чем больше ссылок с других страниц, тем выше вероятность важности страницы. Эта информация может быть распределена по вершинам в графе. Дискретно-временной процесс Маркова в качестве модели сёрфинга имитирует случайное блуждание пользователя по графу и после этого рассчитывается важность веб-страницы как стационарное распределение вероятностей процесса Маркова. HITS основан на хабах и авторити-документах для моделирования двух аспектов важности веб-страницы. Hub-страница – это та, с которой идёт много ссылок на другие страницы, а authority-страница – та, на которую ссылаются множество Hub-страниц. Принципиально, хорошие хабы ссылаются на хорошие authorities и наоборот. Исследования показали, что HITS так же хорош, как и PageRank [1]. Было разработано много алгоритмов для улучшения точности и эффективности PageRank. Одни работы концентрировались на ускорении вычислений [9, 17], другие – на совершенствовании и расширении алгоритма, например, тематический PageRank [12] и запросо-зависимый PageRank [20]. Основной идеей этих алгоритмов является учёт темы и предположение, что если одобрение (ссылка) страницы находится на странице с такой же темой, то вес поддержки увеличивается. Прочие варианты PageRank включают модификацию «персонализированного вектора» [11], изменение «дэмпинг-фактора» [4] и вводят понятие кросс- и внутри-доменного веса ссылок [16]. Кроме того, существуют работы по теоретическим проблемам PageRank [3, 10]. Так же были разработаны алгоритмы ссылочного анализа, направленные против ссылочного спама, к примеру, TrustRank [8] – технология, учитывающая надёжность веб-страниц при расчёте важности. В TrustRank ряд надёжных страниц определяется как seed-страницы. Далее, доверие (trust) seed-страниц распространяется на другие страницы в графе. Так как распространение начинается с доверенных страниц, TrustRank обладает более высоким сопротивлением спаму по сравнению с PageRank.

Поведение пользователя

Многие веб-сервисы обеспечивают помощь пользователям при работе в Сети. Иногда они записывают поведение пользователей с их согласия. Обычно пользователь сёрфит (блуждает) по Сети с потребностью в какой-либо информации. Для захода на новую страницу пользователь может либо кликнуть на гиперссылку на другой странице, либо ввести URL в адресную строку. Пользователь повторяет эти действия до тех пор, пока не найдёт необходимую информацию (или же пока не сдастся). Данные о поведении пользователя могут быть записаны и отражены триадой URL + ВРЕМЯ + ТИП (см. примеры в Таблице 1). Здесь URL отражает адрес посещённой страницы, ВРЕМЯ – длину посещения, а ТИП показывает тип перехода (ВВОД в случае ввода адреса в браузере, КЛИК в случае перехода с предыдущей страницы). Записи сортируются в хронологическом порядке.

Таблица 1. Примеры данных о поведении пользователя.

Из этой информации мы получаем переходы пользователя от страницы к странице и время, проведённое на странице в следующем виде:

Сегментация сессии. Мы обозначаем сессию за логическую единицу сёрфинга пользователя. В данной работе мы используем два правила сегментации сессии. Во-первых, если время старта данной записи составляет 30 минут после предыдущей, то мы считаем данную запись стартом новой сессии [24]. Во-вторых, если типу записи соответствует «ВВОД», то мы считаем данную запись стартом новой сессии. Эти два правила далее называются правило времени и правило типа.

Конструкция пар URL. В каждой сессии мы создаём пары URL из смежных запросов. Пара URL показывает, что пользователь перешёл с первой страницы на вторую при помощи клика по гиперссылке.

Оценка вероятности сброса. Для каждой сессии, сегментированной правилом типа, первый URL напрямую вводится пользователем. Следовательно, такой URL «безопасен» и называется зелёным трафиком (green traffic). Стоит отметить, что пользователи часто посещают страницы, набирая URL из закладок в браузерах. Эти страницы классифицируются как зелёный трафик, так как они безопасны, интересны и/или важны для пользователей. При обработке поведенческих данных мы считаем такие URL целями случайного сброса (когда пользователь больше не хочет блуждать по сети по гиперссылкам). Мы нормализуем частоты первых URL в таких сессиях для получения вероятности сброса (reset probability) соответствующих веб-страниц.

Извлечение времени посещения. Для каждой пары URL мы используем разность во времени между посещением второй и первой страницы. Эта разность является наблюдаемым временным интервалом посещения первой страницы. Для последней страницы в сессии мы используем для расчёта времени посещения следующую логику: если сессия сегментирована правилом времени, мы случайным образом выбираем временной промежуток из распределения наблюдаемых интервалов посещения. Если же сессия сегментирована правилом типа, мы используем разность между временем посещения последней страницы и стартом новой сессии (страница типа ВВОД) в качестве времени посещения.

Обобщая информацию о переходах и времени посещения, мы способны построить граф сёрфинга пользователей (см. Рисунок 1). Каждая вершина графа отражена URL в данных о поведении пользователя, объединёнными с вероятностью сброса и временем посещения в виде мета-данных. Каждое ориентированное ребро отражено переходом между двумя вершинами, объединённым с числом переходов в виде веса. Другими словами, граф сёрфинга пользователей является взвешенным графом с вершинами, содержащими мета-данными, а рёбрами – содержащими веса. Мы определили его как G = <V, W, T, σ>, где V = {v_i}, W = {w_ij}, T = {T_i}, σ = {σ_i}, (i,j = 1,…, N) являются соответственно вершинами, весами рёбер, интервалами посещения и вероятностями сброса. N является числом веб-страниц в графе сёрфинга пользователя.

Модель

Для более точной обработки информации о времени посещения мы предлагаем ввести непрерывно-временной однородный по времени процесс Маркова для имитации случайного блуждания по графу сёрфинга.

Допущения

При использовании новой модели, необходимо сделать ряд следующих допущений:

1. Независимость пользователей и сессий. Процессы блуждания разных пользователей в разных сессиях не зависят друг от друга. Другими словами, мы рассматриваем блуждание по сети как стохастический процесс, в котором данные пользователя в каждой сессии являются i.i.d. (независимыми и одинаково распределёнными) образцами процесса. Это допущение независимости широко используется в статистике при оценке параметров в данных.
2. Свойство Маркова. Страница, которую пользователь посетит следующий зависит только от нынешней страницы и не зависит от ранее посещённых страниц. Это допущение является основным в алгоритме PageRank.
3. Однородность во времени. Поведение пользователей в сёрфинге (т.е. переходы и длительность посещения) не зависит от времени суток. И хотя в действительности это допущение не совсем верно, оно важно для технической стороны задачи. Стоит отметить, что оно так же является основным допущением в алгоритме PageRank.

На основе этих допущений можно создать непрерывно-временной однородный во времени процесса Маркова для имитации случайного блуждания по графу сёрфинга. Сходно с алгоритмом PageRank, можно использовать стационарное распределение вероятностей этого процесса для оценки важности страниц.

Непрерывно-временная модель Маркова

Предположим, что пользователь в Сети блуждает по всем страницам. За X_s принимаем страницу, которую пользователь посещает за время s, s > 0. Тогда с учётом трёх вышеупомянутых допущений, процесс X = {X_s, s ≥ 0} является непрерывно-временным однородным во времени процессом Маркова. Пусть p_ij(t) будет вероятностью перехода от страницы i к странице j за временной интервал (также называемый временным инкрементом в статистике) t в этом процессе. Можно доказать, что существует стационарное распределение вероятности π, которое является уникальным и не зависит от t [23], объединённое с P(t) = [p_ij(t)]_NxN таким образом, что для любого t > 0 верно

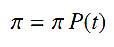
Каждая i-тая запись в распределении π соответствует отношению времени, которое пользователь провёл на i-той странице к времени, проведённому на всех страницах при t → ∞. В таком случае, распределение π является метрикой важности веб-страницы. Для расчёта стационарного распределения вероятностей необходимо определить вероятность в каждой записи матрицы P(t). Однако на практике такую матрицу сложно получить, так как сложно собрать данные обо всех возможных временных интервалах. Для решения этой проблемы мы предлагаем новый алгоритм, который основан на матрице скорости переходов (так же называемой матрицей интенсивности) [23].

Алгоритм BrowseRank

Обзор

Мы используем матрицу скорости переходов для вычисления стационарного распределения вероятностей P(t), чтобы измерить важность веб-страницы. Соответствующий алгоритм называется BrowseRank. Матрица скорости переходов определяется как производная от P(t), где t стремится к нулю, если существует. Тогда Q = P'(0). Мы называем матрицу Q = (qij)NxN Q-матрицей для краткости. Доказано, что когда пространство состояний конечно, существует прямая зависимость между Q-матрицей и P(t), а -∞ < q_ii < 0; Σ_j q_ij = 0 [23]. Из-за зависимости используется Q-процесс для отражения исходного непрерывно-временного процесса Маркова, который является процессом сёрфинга X = {X_s, s ≥ 0}. Он определяется до Q-процесса из-за конечности пространства состояний. У использования Q-матрицы есть два преимущества.

• Параметры Q-матрицы могут быть успешно получены из данных о поведении пользователей.
• На основе Q-матрицы можно эффективно рассчитывать стационарное распределение вероятностей P(t) в соответствии с нижеследующей теоремой.

До рассмотрения теоремы эффективного расчёта стационарного распределения вероятностей Q-процесса, необходимо рассмотреть концепцию встроенной цепи Маркова (embedded Markov chain, EMC) [22] в соответствии с Q-процессом. Так называемая встроенная цепь Маркова – это дискретно-временной процесс Маркова, описанный матрицей вероятностей переходов с нулевыми значениями во всех диагональных позициях и –q_ij/q_ii во всех недиагональных, где параметры имеют те же определения, что были описаны выше.

Теорема 1. Допустим, X – Q-процесс, а Y – EMC, полученная из Q-матрицы. Пусть π = (π₁, … π_N) и аналог с диакритическим знаком ~ определяют стационарное распределение вероятностей процессов X и Y, тогда:

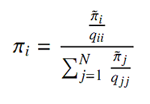
См. [22] для доказательства теоремы.

Стоит отметить, что процесс Y является дискретно-временной цепью Маркова, значит его стационарное распределение вероятностей π^~ может быть легко рассчитано, как в [6].

Расчёт q_ii

В соответствии с [22] для Q-процесса, длительность посещения, равная Ti на i-той вершине, регулируется экспоненциальным распределением q_ii:

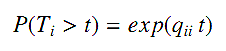
Это значит, что возможна оценка q_ii из большого количества данных о длительности посещений. Однако задача нетривиальна, так как в данных присутствует шумовая погрешность, зависящая от скорости Интернет-соединения, размера страницы, её структуры и прочих факторов. Другими словами, наблюдаемые значения удовлетворяют экспоненциальное распределение не полностью. Чтобы решить эту проблемы, мы используем аддитивную шумовую модель для выражения данных и расчёта независимой и последовательной оценки параметра q_ii. Допустим, дана страница i и есть m_i число наблюдений длительности посещения из данных о поведении пользователя, определённых как Z₁, Z₂, …, Z_mi с таким же распределением, как случайная переменная Z. Без потери общего смысла, мы предполагаем, что Z является комбинацией реальной длительности посещения T_i и шума U.

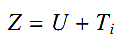
Предположим, что U определяется как распределение хи-квадрат Chi(k), тогда его ожидание и дисперсия равны k и 2k соответственно. Далее, предположим, что ожидание и дисперсия Z равны μ и σ². Допуская, что U и Ti независимы, получаем:

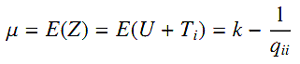
Отметим, что ожидание образца и дисперсия образца независимы и последовательны для μ и σ². Тогда можно оценить qii решив:

Оценка вероятности перехода в EMC

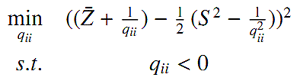
Вероятности перехода в EMC описывают «чистые» переходы пользователя по графу сёрфинга. Их оценка может быть основана на наблюдаемых переходах по страницам в данных о поведении. Так же, можно считать такие переходы зелёным трафиком. Мы используем нижеописанный подход для введения этих двух типов информации в оценку. Допустим, есть пользователь, блуждающий по графу G = [V,W,T,σ]. Мы добавляем псевдо-вершину (N + 1) к G и два типа рёбер: рёбра с последней страницы каждой сессии к псевдо-вершине, связанные с числом кликов последней страницы в виде веса; и рёбра от псевдо-вершины к первой странице каждой сессии в связи с вероятностью сброса. Мы определяем новый граф как G^~ = [V^~,W^~,T,σ^~], где |V|=N+1, σ^~= <σ^~₁,…, σ^~_N,0>. Далее используется модель EMC для случайного блуждания по новому графу G^~. Полагаясь на закон больших чисел, вероятности перехода в EMC будут оценены как:

[Закон больших чисел в теор.вер. утверждает, что среднее арифметическое в большой выборке близко к математическому ожиданию данного распределения.] Очевидное объяснение перехода таково: при блуждании пользователя по графу возможно два варианта. Первый предполагает переход по рёбрам с вероятностью α, второй же – начало новой сессии с вероятностью (1 – α). Выбор новой страницы определяется вероятностью сброса. Одним из преимуществ использования этой формулы для оценки является то, что оценка не будет зависеть от ограниченного числа наблюдаемых переходов. Другим преимуществом является то, что соответствующая EMC примитивна и, как следствие, имеет уникальное стационарное распределение.

Теорема 2. Допустим, X – Q-процесс, а Y – его EMC. Если записи в матрице вероятностей переходов Pтильда определяются как в последней формуле, то процесс Y примитивен, т.е. граф переходов процесса Y сильно связан (что означает наличие прямого пути от любого узла к любому другому узлу в графу).

Доказательство:

Для графа сёрфинга пользователя у нас есть три наблюдения.

1. Имеется вероятность сброса σ_i ≥ 0 для каждого i = 1,2,…,N. Предположим, что среди них есть T строго положительных записей и все сессии имеют первой страницей T-страницу.
2. Так как все страницы в пространстве состояний V рассматриваются из данных о поведении, то они все принадлежат сессии.
3. Сессия соответствует пути в графе переходов: от первой страницы в сессии существует путь ко всем остальным страницам в этой же сессии.

Для любого i, j ∈ V, основанного на втором наблюдении, предполагается, что страница i находится в сессии с первой страницей b_i, а страница j в сессии с первой страницей b_j. Если страница i является последней страницей в сессии, то в соответствии с правилом сброса и первым наблюдением имеется путь перехода с i к b_j с вероятностью σ_bj > 0. Тогда на основании третьего наблюдения, может быть найден путь от b_j к j. В результате имеется прямой путь от i к j. Если страница i не является последней страницей в сессии, то на основании третьего наблюдения, будет иметься путь от i к последней странице в сессии. Так как есть путь от последней страницы в сессии к странице j, фактически можно заключить, что есть прямой путь от i к j. Суммируя, для алгоритма BrowseRank необходимо:

1. Создать граф сёрфинга пользователя на основе данных о его поведении
2. Рассчитать q_ii для всех страниц
3. Рассчитать матрицу вероятностей переходов по цепи Маркова и получить стационарное распределение вероятностей
4. Рассчитать стационарное распределение вероятностей Q-процесса, используя формулу из Теоремы 1