SEO-Константа
Яндекс.Директ + оптимизация
Сетевая структура гиперссылочной среды может быть богатым источником информации о содержании среды, при условии, что у нас есть эффективные средства для ее понимания. Мы разрабатываем комплект инструментов алгоритма для извлечения информации из структуры ссылок таких сред, а также отчет об экспериментах, которые демонстрируют свою эффективность в различных контекстах всемирной паутины. Основной вопрос посвящен очистке широких тем поиска, благодаря открытию «авторитетных» источников информации по таким темам. Мы предложим и проверим принцип разработанного алгоритма авторитетности, основанного на взаимосвязи между количеством релевантных авторитетных страниц и множеством «хаб-страниц», что объединяет их в структуру ссылок. Наша разработка связана с собственными векторами некоторых матриц, которые взаимосвязаны с ссылками графа; эти связи в свою очередь, мотивируют дополнительные эвристические правила для анализа ссылок.
Сетевая структура гиперссылочной среды может быть богатым источником информации о содержании среды, при условии, что у нас есть эффективные средства для ее понимания. В этой работе, мы разрабатываем комплект инструментов алгоритма для извлечения информации из структуры ссылок таких сред, а также отчет об экспериментах, которые демонстрируют свою эффективность в различных контекстах всемирной паутины [4]. В частности, мы обращаем внимание на использование ссылок для анализа набора страниц, относящихся к обширной теме поиска, и для выявления самых «авторитетных» страниц для таких тем.
Хотя наши методы не являются специфическими для веб-сети, проблемы поиска и структурного анализа особенно актуальны для данной области. Интернет является гипертекстовой базой данных огромной сложности, и она продолжает расширяться феноменальными темпами. Кроме того, его можно рассматривать как сложную форму популистской гиперсреды, в которой миллионы онлайн-участников с разнообразными и зачастую противоречащими друг другу целями, постоянно создают гиперссылочный контент. Таким образом, в то время как люди могут навести порядок на весьма локальном уровне, глобальная организация сети совсем не спланированная –– структуры высокого уровня могут выявиться в результате апостериорного анализа.
Наша работа начинается с проблемы поиска в Интернете, которую мы могли бы определить примерно как процесс обнаружения страниц, которые имеют отношение к данному запросу. Качество метода поиска обязательно требует оценки человека, в связи с субъективностью, присущей таким понятиям, как релевантность. Начнем с наблюдения, что улучшение качества методов поиска в сети, в настоящее время, большая и интересная проблема, которая во многом ортогональна вопросам алгоритмической эффективности и сохранения. В частности, считается, что текущая поисковая система обычно занимает значительную часть сети и находит ответ за считанные секунды. Но она была бы весьма полезной для инструментов поиска с более длительным временем реакции, при условии, что результаты будут иметь достаточно большую ценность для пользователя. Но трудно сказать, что такой инструмент поиска должен вычислить в это дополнительное время. Ясно, что нам не хватает критериев выбора, которые определяются конкретно и соответствуют человеческим представлениям о качестве.
Запросы и авторитетные источники. Мы рассматриваем поиск, начиная с запроса от пользователя. Кажется, что лучше всего не унифицировать точки зрения на разные типы запросов, если их количество более чем один, потому что на обработку каждого типа могут потребоваться различные методы. Рассмотрим, например, следующие типы запросов:
Сосредотачиваясь только на первых двух типах запросов на данный момент, мы видим, что они представляют собой разные виды трудностей. Трудность в решении конкретных запросов сконцентрирована, грубо говоря, вокруг того, что можно назвать «Дефицитной проблемой»: существует очень мало страниц, которые содержат необходимую информацию, и часто трудно определить идентичность этих страниц.
Для обширных запросов, с другой стороны, можно найти много тысяч соответствующих страниц, такой набор страниц генерируется вариантами соответствующих терминов (например, кто-то вводит в строку поиска, такие неоднозначные запросы как «Гейтс», «поисковые системы», или «цензура» в поисковых системах, таких как AltaVista [17]), или более сложными способами. Таким образом, проблемы дефицита в данном случае не существует. Вместо этого, основная трудность заключается в том, что можно было бы назвать проблемой избытка: количество страниц, которые можно было бы разумно отнести к релевантным, является слишком большим для восприятия человека. Для обеспечения эффективного метода поиска в этих случаях, необходим способ фильтрации, что бы из огромного числа страницах выбрать небольшой набор самых «авторитетных» или «точных».
Это понятие авторитетности, по отношению к обширным запросам, служит центром внимания нашей работы. Одним из основных трудностей, с которыми мы сталкиваемся в решении этого вопроса, является точное моделирование авторитетности в контексте конкретной темы запроса. Как мы можем определить авторитетная ли страница, что мы отобрали?
Полезно обсудить некоторые из трудностей, которые возникают здесь. Во-первых, рассмотрим непосредственную цель поиска harvard.edu, домашней страницы Гарвардского университета, как одной из наиболее авторитетных страниц для запроса «Гарвард». К сожалению, есть более миллиона страниц в сети, которые используют термин «Гарвард», и в harvard.edu этот термин не используется чаще остальных, ни в качестве текста сайта, ни в любой другой форме, которые способствуют его текстовой ранжирующей функции. Действительно, можно ожидать, что нет чисто внутренней меры страницы, которая позволяет правильно оценить авторитетность. Во-вторых, рассмотрим проблему нахождения домашних страниц основных поисковых систем сети. Можно было бы начать с запроса «поисковики», но непосредственная трудность заключается в том, что многие естественные авторитетные страницы (Yahoo!, Excite, AltaVista) не используют этот термин на своих страницах. Это фундаментальное и повторяющееся явление — другой пример того, что нет оснований ожидать, что домашние страницы Honda или Toyota содержат термин «автопроизводители».
Анализ гиперссылочной структуры. Анализируя гиперссылочную структуру среди веб-страниц, можно прийти к решению многих трудностей, описанных выше. Гиперссылки кодируют значительное количество скрытых человеческих мнений, и мы утверждаем, что такого рода мнения — это именно то, что нужно, чтобы сформулировать понятие авторитетности. В частности, создание ссылки на сайт представляет собой конкретное указание следующих типов суждений: создатель страницы р, ссылаясь на страницу q, возлагает в какой-то мере авторитетность на q. Кроме того, ссылки дают нам возможность найти потенциальную авторитетность чисто по страницам, которые указывают на них; это способствует обходу проблемы, которая обсуждалась выше, так что многие приметные страницы не являются самостоятельно описанными в достаточной мере.
Конечно, есть ряд подводных камней при применении ссылки для таких целей. Прежде всего, ссылки создаются для различных причин, многие из которых не имеют ничего общего с присвоением авторитетности. Например, большое количество ссылок создаются преимущественно для целей навигации («Нажмите здесь, чтобы вернуться в главное меню»), другие представляют собой платную рекламу и/или имеют своей целью продвижение сайтов в поиске.
Другой проблемой является трудность в нахождении необходимого баланса между критериями значимости и популярности, каждый из которых вносит свой вклад в наше интуитивное представление авторитетности. Весьма познавательно рассмотреть серьезные проблемы, присущие следующим простым эвристическим процедурам размещения авторитетных страниц: из всех страниц, содержащих строку запроса, вернуть те, у которых наибольшее количество входящих ссылок. Мы уже утверждали, что для большинства запросов («поисковики», «автопроизводители», …), ряд наиболее авторитетных страниц не содержит соответствующие строки запроса. Наоборот, эта эвристическая процедура будет рассматривать наиболее популярные страницы, такие как yahoo.com или netscape.com, которые являются наиболее авторитетными в отношении любой строки запроса, что в нем содержится.
В этой работе мы предлагаем модель на основе ссылок для присвоения авторитетности, и покажем, как это приводит к методу, который последовательно определяет соответствующие авторитетные веб-страницы для широкого поиска. Наша модель основана на взаимосвязи, которая существует между авторитетными страницами для темы и теми страницами, которые ссылаются на авторитетные — мы называем страницы последнего типа, как хабы. Заметим, что существует некоторое непосредственное равновесие между хабами и авторитетными страницами в графе, который определяется ссылочной структурой, и мы используем это, что бы разработать алгоритм, который одновременно идентифицирует оба типа страниц. Алгоритм сосредоточен на подграфах сети, которые мы строим из выхода текстовой поисковой системы сети, наша методика построения таких подграфов предназначена для создания небольших наборов страниц, которые могут содержать наиболее авторитетные страницы для заданной темы.
Обзор. Наш подход к поиску авторитетных источников сети учитывает ее глобальный характер: мы хотим определить наиболее главные страницы для широкого поиска в контексте сети в целом. Глобальные подходы включают основные проблемы представления и фильтрации больших объемов информации, поскольку весь набор страниц, относящихся к широкому запросу, может иметь размер в миллион страниц. Это отличается от локальных подходов, которые стремятся уловить взаимосвязь между множеством веб-страниц, принадлежащих к одному логическому сайту или интрасети, в таком случае объем данных значительно меньший, а зачастую преобладает другой набор вариантов.
Важно также отметить смысл, в котором наши основные проблемы принципиально отличаются от задач группирования. Группирование рассматривает вопрос о разбивании неоднородной совокупности на подгруппы, которые являются в некотором роде более связанными; в контексте сети, это может быть связано отличием страниц, связанных с различными значениями или смыслами запроса. Таким образом, группирование по своей сути отличается от вопроса извлечения обширных тем путем установления авторитетности, хотя в следующем разделе будет показана некоторая связь. Ибо даже если бы мы могли прекрасно разбивать смыслы неоднозначных терминов запроса (например, «Windows» или «Гейтс»), мы бы до сих пор остались с теми же основными проблемами представления и фильтрации огромного количества страниц, которые имеют отношение для каждого основного смысла этого термина запроса.
Структура работы следующая. Во 2 разделе обсуждается метод, с помощью которого мы создаем сфокусированный подграф сети по отношению к обширному поиску, создавая набор релевантных страниц с большой вероятностью авторитетности. В 3 и 4 разделах мы рассмотрим наш основной алгоритм для определения хабов и авторитетных страниц в таком подграфе, и некоторые применения этого алгоритма. В 5 разделе рассматривается связь с соответствующими работами в области веб-поиска, библиометрическими, и изучением социальных сетей. В 6 разделе описывается, как расширение нашего основного алгоритма создает несколько наборов хабов и авторитетных страниц в рамках общей ссылочной структуры. Наконец, в 7 разделе исследуется вопрос о том, какой должна быть «обширная» тема, чтобы наш метод был эффективным, и в 8 разделе рассматриваются некоторые работы, которые были проделаны для оценки представленного здесь метода.
Мы можем рассматривать любой набор гиперссылочных страниц V, как ориентированный граф G = (V, E): узлы соответствуют страницам, и направленное ребро (p, q) ∈ E указывает на наличие связи от р к q. Можно сказать, что исходящая степень узла p — это число узлов, которые имеют исходящие ссылки, и входящая степень узла р — число узлов, которые имеют входящие ссылки. От графа G, мы можем выделить небольшие части, или подграфы, следующим образом. Если W ⊆ V является подмножеством страниц, мы используем G [W], чтобы граф, связанный с W: его узлы – это страницы в W, а его ребра соответствуют всем ссылкам между страницами в W.
Пусть дан обширный запрос, заданный строкой запроса σ. Мы хотим определить авторитетные страницы, анализируя ссылочную структуру, но сначала мы должны определить подграф сети, на которой будет работать наш алгоритм. Наша цель — сосредоточить вычислительные усилия на соответствующих страницах. Так, например, мы могли бы ограничиться рассмотрением множества Qσ всех страниц, содержащих строку запроса, но это имеет два существенных недостатка. Во-первых, этот набор может содержать более миллиона страниц, и, следовательно, влечет за собой значительные вычислительные затраты, а во-вторых, как мы уже говорили, большинство из лучших авторитетных страниц не принадлежит этому множеству.
В идеале, мы хотели бы сосредоточить внимание на множестве страниц Sσ со следующими свойствами:
Поддерживая небольшой размер Sσ, мы можем позволить себе вычислительные затраты для применения нетривиальных алгоритмов, обеспечив большое количество соответствующих страниц, нам легче будет найти качественные авторитетные страницы, так как они, вероятно, будут сильно связаны в Sσ.
Как мы можем подобрать такой набор страниц? Для параметра t (обычно составляет около 200), мы сначала собираем t страницы с наиболее высоким рейтингом для запроса σ из текстовых поисковых систем, таких как AltaVista [17] или Hotbot [57]. Мы будем обращаться к этим t страницам в качестве корневого набора Rσ. Этот корневой набор удовлетворяет условиям (1) и (2), перечисленным выше, но он совсем не соответствует требованию (3). Чтобы убедиться в этом, заметим, что важнейшие t страницы, что возвращаются текстовыми поисковыми системами, которые мы используем, будут содержать строку запроса σ и, следовательно, Rσ является подмножеством набора Qσ всех страниц, содержащих σ. Выше мы утверждали, что даже Qσ часто не удовлетворяют условию (3). Интересно также заметить, что часто ссылок между страницами в Rσ крайне мало, что делает его по существу «бесструктурным». Например, в наших экспериментах, корневой набор для запроса «Java» содержал 15 ссылок между страницами в различных доменах; корневой набор для запроса «цензура» содержал 28 ссылок между страницами в различных доменах. Эти цифры являются типичными для различных испробованных запросов, их можно сравнить с 200 • 199 = 39 800 потенциальными ссылками, которые могут существовать между страницами в корневом наборе.
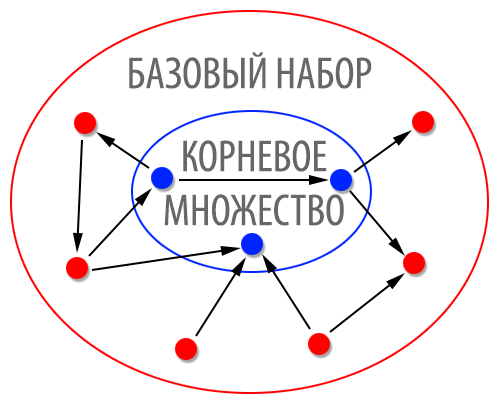
Рис 1. Расширение корневого множества релевантных страниц в базовом наборе.
Мы можем использовать корневой набор Rσ, однако, что бы составить набор страниц Sσ, которые будут удовлетворять нашим условиям поиска. Рассмотрим наиболее авторитетную страницу для темы запроса — хотя ее может и не быть в наборе Rσ, но она должна соответствовать, по меньшей мере, одной странице в Rσ. Следовательно, мы можем увеличить число наиболее авторитетных страниц в нашем подграфе за счет расширения входящих и исходящих ссылок Rσ. Конкретно это определяется следующим образом:

Таким образом, мы получаем Sσ, путем роста Rσ, что бы включить любую страницу, на которую ссылается страница в Rσ, и страницу, которая ссылается на страницу в Rσ — с условием, что мы допускаем одну страницу в Rσ, которая дает больше d страниц, указывающих на них в Sσ. Этот последний пункт имеет решающее значение, поскольку на ряд веб-страниц указывают несколько сотен тысяч страниц, и мы не можем включить их всех в Sσ, если мы хотим, чтобы его размер был достаточно малым.
Для нас Sσ — базовое множество для σ; в наших экспериментах мы построим его, применяя процедуры подграфа с помощью поисковой системы AltaVista, t = 200, d = 50. Мы считаем, что Sσ обычно удовлетворяет требованиям пунктов (1), (2) и (3), описанных выше — его размер, как правило, находится в диапазоне 1000-5000; и, как мы упоминали выше, на наиболее авторитетную страницу должна ссылать хотя бы одна из 200 страниц в корневом наборе Rσ для того, чтобы она была добавлена к Sσ.
В следующем разделе мы опишем наш алгоритм для вычисления хабов и авторитетных страниц в базовом множестве Sσ. Прежде чем перейти к этому, мы обсудим эвристические процедуры, которые очень полезны для противостояния действию ссылок, которые имеют лишь навигационную функцию. Во-первых, пусть G[Sσ] обозначает, как и выше, подграф, индуцированный на страницах Sσ. Мы различаем два типа связей в G[Sσ]. Можно сказать, что ссылка является поперечной, если она находится между страницами с различными доменными именами, и внутренней, если она находится между страницами с одинаковым доменным именем. Под «доменным именем» мы имеем в виду здесь первый уровень в URL строке, связанной со страницей. Поскольку внутренние ссылки очень часто существуют чисто для обеспечения навигации по инфраструктуре сайта, то они передают гораздо меньше информации, чем поперечные ссылки об авторитетности страниц, на которые они указывают. Таким образом, мы удаляем все внутренние ссылки с графом G[Sσ], сохраняя только ребра, соответствующие поперечным ссылкам, в результате чего мы получаем граф Gσ.
Это очень простая эвристическая процедура, но мы находим ее эффективной для устранения многих отклонений, вызванных обработкой навигационных ссылок тем же способом, что и для других ссылок. Есть и другие простые эвристические процедуры, которые могут быть полезны для устранения ссылок, которые, интуитивно не относятся к авторитетным. То, что стоит упомянуть, основано на следующем наблюдении. Предположим, что большое количество страниц с одного домена указывают на одну страницу р. Довольно часто это соответствует нагромождению поддержек, рекламы, или какого-то другого типа «соглашений» между ссылающимися страницами, например, фраза «Этот сайт разработан …» и соответствующие ссылки внизу каждой страницы в данном домене. Для устранения этого явления, мы можем ввести параметр m (обычно m ≈ 4-8) и он соответствует только страницам из одного домена, чтобы указать на любую данную страницу p. Опять же, это может быть эффективной эвристической процедурой, в некоторых случаях, хотя мы не использовали это при выполнении следующих экспериментов.
Метод, описанный в предыдущем разделе, включает создание небольшого подграфа Gσ, который относительно сосредоточен на теме запроса — он имеет много релевантных и достаточно авторитетных страниц. Обратимся теперь к проблеме извлечения этих авторитетных страниц из общего набора, непосредственно основываясь на анализе ссылочной структуры Gσ.
Самый простой подход, возможно, упорядочивал бы страницы по их входящей степени в Gσ (количеству ссылок, указывающих на них). Мы отказались от этой идеи раньше, когда она была применена к набору всех страниц, содержащих слова запроса σ, но теперь мы явно построили небольшой набор соответствующих страниц, содержащих большее количество авторитетных страниц, которые мы хотели бы найти. Таким образом, эти авторитетные страницы принадлежат к Gσ и на них, в значительной степени, ссылаются страницы в Gσ.
Действительно, подход ранжирования по входящей степени обычно работают намного лучше в контексте Gσ, чем по предыдущим параметрам, которые мы рассмотрели; в некоторых случаях, он может дать очень качественные результаты. Тем не менее, подход все же имеет некоторые существенные проблемы. Например, на запрос «java», страницы с большой входящей степенью состоит из gamelan.com и java.sun.com, вместе со страницами, рекламирующими отдых на Карибах, и главной страницей Amazon Books. Это смешение является типом проблем, которые возникают при этой простой схеме ранжирования. В то время как первые две из этих страниц, безусловно, следует рассматривать как «хорошие» ответы, другие не относятся к теме запроса; они имеют большую входящую степень, но не имеют тематического единства. Эта основная трудность влечет за собой напряжение в подграфе Gσ между авторитетными страницами и страницами, которые являются просто «общепопулярными»; мы ожидаем, что последний тип страниц будут иметь большую входящую степень независимо от заданной темы запроса.
Можно подумать, что избежание этих трудностей требует дальнейшего использования текстового содержимого страниц в базовом наборе, а не только ссылочной структуры. Покажем, что это не так — на самом деле можно извлечь информацию из ссылок более эффективно — и мы начнем со следующего наблюдения. Авторитетные страницы, имеющие отношение к первоначальному запросу должны не только иметь большую входящую степень; а так как все они являются авторитетными для общих тем, должно быть значительное перекрытие в наборе страниц, которые ссылаются на них. Таким образом, в дополнение к наиболее авторитетным страницам, мы ожидаем найти то, что можно было бы назвать хабами: эти страницы имеют ссылки на несколько соответствующих авторитетных страниц. Именно этим страницы, которые «сближают» авторитетные страницы для общих тем, и позволяют исключать несвязанные страницы с большой входящей степенью. (Основной пример изображен на рисунке 2; в реальности, конечно, картина не такая четкая).
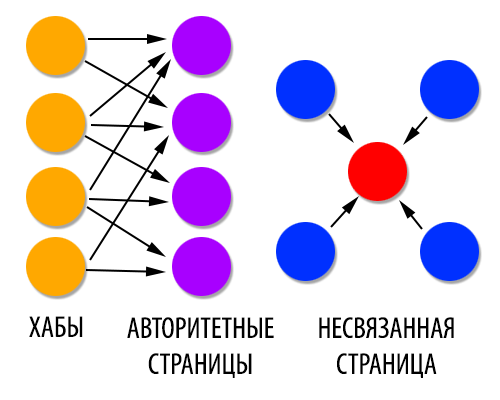
Рис. 2. Плотно связанный набор хабов и авторитетных страниц
Хабы и авторитетные страницы демонстрируют то, что можно было бы назвать взаимодополняющей взаимосвязью: «хороший» хаб –– это страница, которая ссылается на много авторитетных страниц; «хорошая» авторитетная страница –– это страница, на которую ссылаются много «хороших» хабов. Ясно, что если мы хотим определить хабы и авторитетные страницы в подграфе Gσ, нам нужен метод для взлома этого замкнутого круга.
Итерационный алгоритм. Мы используем связь между хабами и авторитетными страницами с помощью итерационного алгоритма, который поддерживает и обновляет численный вес каждой страницы. Таким образом, с каждой страницей р, мы связываем неотрицательный вес авторитетной страницы x(p) и неотрицательный вес хаба y(p). Мы сохраняем постоянность так, что веса каждого типа, нормированные следующим образом и их квадраты ровняются 1: ∑p∈Sσ(x(p))2=1 и ∑p∈Sσ(y(p))2=1. Мы считаем, что страницы с большими х-и у-значениями являются «лучшими» авторитетными страницами и хабами соответственно.
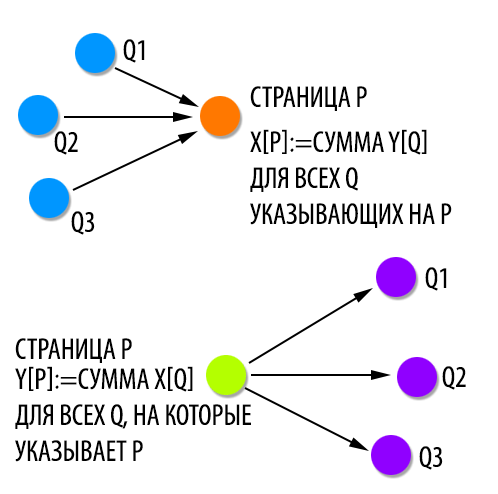
Естественно численно выражать взаимодополняющие связи между хабами и авторитетными страницами следующим образом: если р ссылается на многие страницы с большим х-значением, то она должна иметь большое y-значение; и наоборот, если р ссылается на многие страницы с большим у-значением, то она должна иметь большое х-значение. Это мотивирует двух операций определения веса, которые мы обозначим как I и O. Учитывая веса {x(p)}, {y(p)}, I операция обновляет х-веса следующим образом:
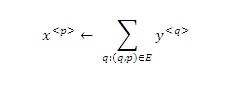
O операция обновляет y -веса следующим образом:
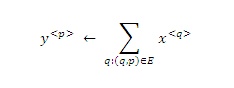
Таким образом, I и O являются основным средством взаимного усиления хабов и авторитетных страниц. (см. рисунок 3).
Теперь, чтобы найти нужное значение «равновесия» для весов, можно применить I и O операции двусторонним способом, и убедиться в том, что будет достигнута реперная точка. Теперь мы можем сформулировать версию нашего основного алгоритма. Мы представляем множество весов {x(p)} в качестве вектора х с координатой для каждой страницы в Gσ; аналогично, мы представляем множество весов { y(p)} как вектор у.

Эту процедуру можно использовать, чтобы удалить максимум c авторитетных страниц и максимум c хабов следующим простым путем.

Мы будем применять процедуру удаления с G равным Gσ, и обычно с с ≈ 5-10. Для решения вопроса о том, как лучше выбрать значение к (число итераций), мы впервые показали то, что если применять итерацию со сколь угодно большим значением к, последовательности векторов {х} и {у} сходятся к фиксированным точкам х* и у*.
Нам понадобятся следующие понятия из линейной алгебры, и мы отсылаем читателя к литературе, такой как [30] для пополнения знаний. Пусть М – симметричная матрица n х n. Собственное значение M представляет собой число λ с тем свойством, что для некоторого вектора ω, мы имеем Мω = λω. Множество всех таких ω является подпространством Rn, которое мы называем собственным пространством, связанным с λ; размерность этого пространства будет определяться кратностью λ. Стандартным является факт, что M имеет не более n различных собственных значений, каждое из которых является действительным числом, и сумма их кратности и есть n. Мы обозначим эти собственные значения λ1(M),λ2(M),…,λn(M), которые индексируются в порядке убывания абсолютной величины, и с каждое собственное значение, перечисленное несколько раз, равняется его кратности. Для каждого отдельного собственного значения, выбираем ортонормированный базис собственного пространства, учитывая, векторы во всех этих базах, мы получим множество собственных векторов ω1(M),ω2(M),…,ωn(M), которые мы можем индексировать таким образом, что ωi(M) принадлежит собственному пространству λi(M).
Для простоты, мы проделаем следующие технические предранжирование для всех матриц, с которыми мы имеем дело: (†)|λ1(M)|>|λ2(M)|.
Если это предположение справедливо, то принимаем ω1(M) в качестве основного собственного вектора, а все остальные ωi(M) как неосновных собственных векторов. Если предположение не выполняется, анализ становится менее аккуратным, но это не влияет никаким существенным образом.
Докажем, что итерация сходится при произвольном увеличении k.
Теорема 3.1. Последовательности x1,x2,x3,… и y1,y2,y3,… сходятся (в пределах х* и у* соответственно).
Доказательство. Пусть G = (V, E), с {p1,p2,…,pn}, и пусть А – матрица смежности графа G; (i,j)-ые элементы А равны 1 если (pi,pj) является ребрами G, и равны 0 в противном случае. Легко проверить, что I и O операции могут быть записаны как х ← ATy и у ← Ах соответственно. Таким образом, хк –– единичный вектор в направлении (ATA)k−1ATz, и ук –единичный вектор в направлении (AAT)kz.
Теперь, стандартный результат линейной алгебры (например, [30]) утверждает, что если M является симметричной n х n матрицей, а v – не ортогональный вектор к главному собственному вектору ω1(M), то единичный вектор в направлении Mkv сходится к ω1(M), если к возрастает неограниченно. Также (как следствие), если M имеет только неотрицательные элементы, то главный собственный вектор M имеет только неотрицательные значения.
Следовательно, z не ортогональна ω1(AAT), и, следовательно, последовательность {yk}сходится к пределу y∗. Аналогично можно показать, что если λ1(ATA) ≠ 0 (как это обусловлено гипотезой (†)), то ATz не ортогонально ω1(ATA). Отсюда следует, что последовательность {xk} сходится к пределу х*.
Доказательство теоремы 3.1 дает следующие дополнительные результаты (в приведенных выше обозначениях).
Теорема 3.2 (С учетом предранга (†).)x∗ является главным собственным вектором ATA, и у* является главным собственным вектором AAT.
В наших экспериментах, мы установим, что сходимость итераций происходит достаточно быстро; практически всегда считается, что к = 20 является достаточным для наибольших значений координат каждого вектора, чтобы они стали неизменными, для значений с в диапазоне, который мы используем. Конечно, теорема 3.2 показывает, что можно использовать любой собственный вектор алгоритма для вычисления реперных точек х* и у*; мы придерживались вышесказанного изложения с точки зрения процедуры итерации по двум причинам. Во-первых, это подчеркивает основную мотивацию нашего подхода с точки зрения усиления I и O операций. Во-вторых, не нужно запускать вышеуказанный процесс повторных I/O операций для конвергенции; нужно просто вычислить веса {x(p)} и {y(p)}, исходя из любого начального вектора x0 и y0, а также найти постоянные лимитированные числа I и O операций.
Основные результаты. Приведем теперь некоторые примеры результатов, полученных с помощью алгоритма, используя некоторые запросы, приведенные во введении.




Среди всех этих страниц, была всего одна, что входит в соответствующий корневой набор Rσ, –– roadahead.com/, при запросе «Гейтс», она заняла в рейтинге сто двадцать третье место при поиске в AltaVista. Это естественно, учитывая тот факт, что многие из этих страниц не содержат никаких признаков начальной строки запроса.
Здесь стоит поразмыслить о двух дополнительных точках. Во-первых, наша единственная польза текстового содержимого страниц заключалась в том, что первоначальный «черный ящик» обращается к текстовой поисковой системе, которая создала корневой набор Rσ. После этого, анализ проигнорировал текстовое содержание страницы. То, что мы хотим сделать здесь, не является тем текстом, который больше всего игнорируется при поиске авторитетных страниц; ясно, что это может быть достигнуто путем интеграции текстового и ссылочного анализов, и мы рассмотрим это в следующем разделе. Тем не менее, результаты, указанные выше, показывают, что значительное количество может быть достигнуто путем только одного анализа ссылочной структуры.
Во-вторых, для многих обширных тем поиска, наш алгоритм выдает страницы, которые могут законно считаться авторитетными по отношению к сети в целом, несмотря на то, что они действует без прямого доступа к крупномасштабному индексу сети. Скорее, есть только «глобальный» доступ к сети через текстовые поисковые системы, такие как AltaVista, от которых достаточно трудно непосредственно получить «адекватных» кандидатов на авторитетные страницы для большинства запросов. Какие результаты означают, что можно надежно оценить некоторые виды глобальной информации в сети, используя только стандартный интерфейс поисковой машины? Глобальный анализ полной ссылочной структуры сети может быть заменен гораздо более локальным методом анализа узко сосредоточенным на подграфе.
Алгоритм, разработанный в предыдущем разделе, может быть применен для других типов проблем — использования ссылочной структуры, что бы получить понятие «сходство» между страницами. Предположим, что мы нашли страницу p, которая представляет интерес — возможно, это авторитетная страница на интересующую нас тему — и мы хотели бы задать вопрос следующего типа: Что пользователями сети считают связанным с р, когда они создают страницы и гиперссылки?
Если р является страницей, которая имеет много ссылок, то считается, что есть проблема избытка: окружающая ссылочная структура будет косвенно представлять собой большое число независимых мнений о взаимосвязи p с другими страницами. Используя наши понятия хабов и авторитетных страниц, мы можем обеспечить подход к вопросу о сходстве страниц, задаваясь вопросом: какие страницы являются наиболее авторитетными в локальной области ссылочной структуры вблизи к р? Такие авторитетные страницы могут потенциально выступать в качестве сводки обширных тем для страниц, связанных с р.
В самом деле, метод, описанный в 2 и 3разделах, может быть адаптирован к этим условиям практически без изменений. Ранее, мы начинали поиск со строки запроса σ; наша просьба от основной поисковой машины была «Найти t страницы, содержащие строку σ». Сейчас мы начинаем со страницы р и ставим следующий запрос к поисковой системе: «Найти t страницы, указывающие на р». Таким образом, мы собираем корневой набор Rp, состоящий из t страниц, которые ссылаются на р; это разрастается в базовый набор Sp как и раньше; и в результате получится подграф Gp, в котором мы можем искать хабы и авторитетные страницы.
На первый взгляд, набор вопросов при работе с подграфом Gp несколько отличается от тех, что участвуют в работе с подграфом, который определяется строкой запроса; однако, мы обнаружили, что большинство из основных выводов, которые мы сделали в двух предыдущих разделах, продолжают применяться. Во-первых, заметим, что рейтинг страниц в Gp в полустепени захода еще не удовлетворителен; рассмотрим, например, результаты этой эвристической процедуры, когда начальная страница р была honda.com, на домашней странице компании Honda Motor.

В большинстве случаях, «топовые» хабы и авторитетные страницы, вычисленные с помощью нашего алгоритма на графе Gp могут быть достаточно очевидными. Мы покажем «топовые» авторитетные страницы, полученные для начальной страницы p honda.com и nyse.com, домашней страницы New York Stock Exchange.

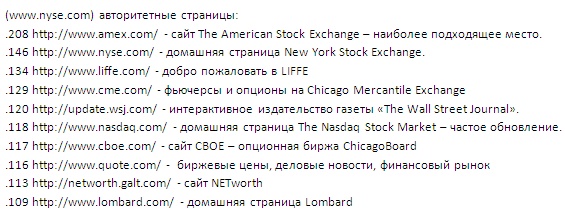
Обратите внимание на трудности, связанные с составлением таких списков при помощи текстовых методов: многие из перечисленных выше страниц почти полностью состоят из фотографий и имеют очень мало текста; а текст, который они содержат, слабо совмещенный. Наш подход, с другой стороны, заключается, через наличие ссылок, в определении того, что создатели веб-страниц, как правило, «классифицируют» вместе с данными страницами honda.com и nyse.com.
Анализ ссылочных структур с целью понимания их социальной или информационной организации был проблемой в ряде взаимных областей. В этом разделе мы рассмотрим некоторые подходы, которые были предложены и разделены на три основных направления. Первое, и наиболее тесно связанное с нашей работой, мы обсудим исследования по использованию ссылочной структуры для определения понятия ранга, эффекта и влияния — мер, с той же мотивацией, как и наше представление об авторитетности. Затем мы обсудим другие способы, в которых ссылки были интегрированы в гипертекст и методы сетевого поиска. Наконец, мы рассмотрим некоторые работы, которые использовали ссылочную структуру для точного группирования данных.
Социальные сети. С помощью изучения социальных сетей было разработано несколько способов измерения относительного ранга — грубо говоря, «значения» — физических лиц в косвенно заданной сети. Мы можем представить сеть, как и выше, графом G = (V, E); ребро (i, j) примерно соответствует «подтверждению» j от i. Это согласуется с нашей интуицией, о которой мы уже упоминали при рассмотрении роли веб гиперссылок в качестве представителя авторитетной страницы. Ссылки могут иметь разные (неотрицательные) веса, соответственно с потенциалом различных подтверждений; пусть А – матрица, чьи (i, j)-ые элементы представляют потенциал подтверждения от узла i ∈ V к узлу j ∈ V.
Кац [35] предложил способ измерения ранга на основе расчетного пути, обобщая его на основе рейтинга полустепени захода. Для узлов, i и j, давайте обозначим Pij(r) числом путей с длиной равной r от i к j. Пусть b<1 – константа, с достаточно малым значением, чтобы Qij=∑r=1∞brPij(r) сходилось для каждой пары (i, j). Теперь Кац определяет sj, ранг узла j, как ΣiQij — ранг в данной модели, основан на общем числе путей, которые заканчиваются в узле j и взвешиваются экспоненциально убывающим коэффициентом затухания. Не трудно получить формулировку сквозной матрицы для этого измерения: sj пропорционально сумме j-ых столбцов матрицы (I − bA)−1 − I, где I обозначает единичную матрицу, а все элементы А равны 0 или 1.
Хаббл [32] предложил аналогичную модель ранга путем изучения равновесия схемы расширения веса на узлах сети. Напомним, что Aij, (i, j)-ые элементы нашей матрицы А, представляют собой потенциал подтверждения от i к j. Пусть ej обозначает априорную оценку состояния узла j. Тогда Хаббл определяет ранги {sj} как множество значений, так что процесс подтверждения вводит тип равновесия — общее «количество» подтверждений входа в узел j, взвешенное по рангу подтверждения; равное рангу j. Таким образом, ранги являются решением системы уравнений sj = ej +ΣiAijsi, для = 1, …, n. Если е обозначает вектор значений {ej}, то вектор ранга в этой модели может быть показан как (I − AT)−1e.
Прежде чем говорить о связи этих измерений с нашей работой, мы рассмотрим, каким образом были продолжены исследования в области библиометрии.
Научные источники. Библиометрия [22] изучает письменные документы и их структуру цитирования. Исследования в библиометрии давно связаны с использованием цитат, чтобы провести количественную оценку важности и «эффекта» отдельных научных работ и журналов, аналогов нашему понятию авторитетности. В этом смысле они касаются оценки ранга конкретного типа социальной сети, которые как газеты или журналы, связаны цитатами (ссылками).
Наиболее известными методами измерения в этой области являются импакт-фактор Гарфилда [26], который используется для численной оценки журналов в издательстве Института научной информации «Journal Citation Reports». Согласно стандартному определению, импакт-фактор журнала j в данном году – это среднее число цитирований статьями, опубликованных за предыдущие два года в журнала j [22]. Оставим сейчас вопрос о том, является ли срок в два года соответствующим периодом для измерения (см., например, работы Егга [21]). Мы видим, что импакт-фактор –– это ранжированное измерение, основанное, в основном, на чистом подсчете входящей полустепени узлов в сети.
Пинский и Нарин [45] предложили более очевидное измерение ранга, основанное на цитатах, вытекающие из наблюдения того, что не все ссылки одинаково важны. Они утверждали, что журнал является «влиятельным», если он, рекурсивно, сильно цитируется другими влиятельными журналами. Можно различить естественную параллель между этой и нашей самоссылающейся конструкции хабов и авторитетных станиц; мы обсудим взаимосвязь ниже. Конкретная конструкция Пинского и Нарина с изменениями, внесенными Геллером [27], заключается в следующем. Измерение ранга журнала называться весом влияния и обозначается wj. Матрица А прочности связи будет иметь элементы заданные следующим образом: Aij обозначает долю цитат из журнала i к журналу j. Согласно неформальному определению, приведенному выше, влияние j должна равняться сумме влияния всех цитирований журнала j, с суммой взвешенной количеством каждый цитаты j. Таким образом, множество мер влияния {wj} создано, чтобы не было нулевого или отрицательного решения системы уравнений wj = ΣiAijwi; и, следовательно, если w — вектор меры влияния, то w ≥ 0, w ≠ 0, и ATw = w. Это означает, что w является основным собственным вектором AT. Геллер [27] заметил, что веса влияние соответствуют стационарному распределению следующего случайного процесса: начиная с произвольного журнала j, выбирается случайная ссылка, которая появилась в j и производится переход в журнал, указанный в ссылке. Дориан [19, 20] показал, что можно измерить ранг, что очень близко соответствует мере влияния, путем неоднократной итерации вычислений, лежащих в основе измерений ранга по методике Хаббла: в первой итерации вычисляются ранги Хаббла {sj} из априорных весов {ej}; {sj} затем становится априорным оцениванием для следующей итерации. Наконец, была работа, направленная на решение вопроса о том, как справиться с самоцитированием журнала (диагональные элементы матрицы A); см., например, де Солла Приса[15] и Нома [42].
Рассмотрим связь между этой и предыдущими работами и нашим алгоритмом для вычисления хабов и авторитетных страниц. Мы также начнем с рассмотрения того, что в чистый подсчет входящей полустепени, что используется в импакт-факторе, является слишком грубым измерением для наших целей, и мы стремимся найти равновесие между относительными рангами узлов, основанных на ссылках. Но сеть и научная литература руководствуются совсем разными принципами, и этот контраст сильно заметен в различии между методикой Пинского и Нарина о вычислении веса влияния и весами хаб / авторитетная страница, которые мы вычисляем. Журналы в научной литературе, на первый взгляд, имеют общую цель, и традиции, такие как процесс экспертной оценки обычно обращает внимание на то, что весьма авторитетные журналы ссылаются друг на друга достаточно часто. Таким образом, есть смысл рассмотреть одноуровневую модель, в которой авторитетные источники напрямую поддерживают другие авторитетные страницы. С другой стороны сеть гораздо более разнородна, веб-страницы имеют множество различных функций – персональные пользователи AOL имеют домашние страницы, и транснациональные корпорации имеют домашние страницы. Кроме того, для широкого круга вопросов, самые авторитетные источники сознательно не связываются друг с другом — сравните, например, домашние страницы поисковых систем и автомобильных производителей, перечисленные выше. Таким образом, они могут быть связаны промежуточным слоем относительно анонимными хабами, которые ссылаются коррелированным способом с тематически связанными наборами авторитетных источников; и наша модель для определения авторитетных страниц сети принимает это во внимание. Существует два уровня ссылочной структуры как среди множества хабов, которые могут не знать о существовании друг друга, и множества авторитетных страниц, которые не желают признавать существования друг друга.
Гипертекст и ранжирование. Существовало несколько методов ранжирования страниц в контексте гипертекста и веба. В работе, предшествовавшей появлению веба, Ботафого, Ривлин, а Шнейдерман [7] работали с целенаправленной автономной средой гипертекста. Они определили понятие индексных узлов и исходных узлы — индексным узлом является тот, у которого исходящая полустепень значительно больше средней исходящей полустепени, а исходным узлом является тот, у которого входящая полустепень значительно больше средней входящей полустепени. Они также предложили измерение, полностью основанные на расстоянии между узлами, которые определяются в графе ссылочной структурой.
Карьер и Казман [9] предложили измерение рангов веб-страниц в целях переупорядочивания результатов поиска. Ранг страниц в их модели равен сумме их входящей и исходящей полустепеней; так используется «хаотическая» версия ссылочной структуры веба.
Оба эти метода в основном основаны на полустепенях узла, параллельно структуры импакт-фактора по Гарфильду. С другой стороны, Брин и Пейдж [8] недавно предложили a измерение рангов, основанное на схеме распределения весов от узла к узлу и ее анализе при помощи собственных векторов. Они начали с модели случайного перехода пользователя по гиперссылкам: на каждой странице пользователь либо выбирает случайную исходящую ссылку, либо (с вероятностью p<1) переходит к новой случайной веб-странице. Стационарная вероятность узла i в этом случайном процессе будет соответствовать “рангу” i, которая является рангом страницы.
С другой стороны можно рассмотреть ранг страниц как соотношение аналогичного процесса в определении веса ранга Пинского-Нарина, с учетом “случайного перехода” к выбранной странице. Если предположить, что веб содержит n страниц, то пусть A обозначает матрицу инцидентности сети n х n, и пусть di обозначает исходящую полустепень узла i, вероятность перехода от страницы i к странице j в модели Брина-Пейджа равняется A´ij = pn−1 +(1− p)di−1Aij. Пусть А’ — матрица, элементами которой являются A’ij. Тогда вектор рангов не ровняется нулю и имеет неотрицательный результат для (A´)Tr = r, и, следовательно, соответствует основному собственному вектору (A´)T.
Одной из основной разницей между нашим подходом и методом PageRank является то, что (согласно формулировке Пинского и Нарина веса влияния) последний основан на модели, в которой авторитетный источник передается непосредственно от одних авторитетных источников к другим, без промежуточных хабов. Использование модели случайного перехода Брина и Пейджа для равномерно выбранных страниц является способом решения полученной проблемы того, что многие авторитетные страницы являются по существу «тупиками» в процессе их распознавания.
Стоит также отметить, основное отличие в применении этих подходов для веб-поиска. В работах [8], алгоритм page-rank применяется для вычисления рангов всех узлов в 24 миллионов веб-страницах; эти ранги затем используются для упорядочения результатов последующих текстовых поисков. Наше использование хабов и авторитетных страниц, с другой стороны, происходит без прямого доступа к веб-индексу; в ответ на запрос, наш алгоритм сначала применяет текстовый поиск, а затем вычисляет численные значения страниц в относительно небольшом подграфе, построенном на результатах первого поиска.
Фриз [25] рассмотрел проблему поиска документов в единоличных и самостоятельных работах гипертекста. Он предложил основные эвристические процедуры, с помощью которых гиперссылки могут повысить понятие актуальности и, следовательно, провести выборочные эвристические процедуры. В частности, в его концепции, актуальность страниц в гипертексте к конкретному запросу основана частично на актуальности тех страниц, на которые они ссылаются. Алгоритм гипертекстового поиска по Маркиори [39] основан на следующей методологии, которая применяется к веб-страницам: коэффициент релевантности для страницы р вычисляется методом, который включает в себя достижимую актуальность страницы р, уменьшающуюся коэффициентом затухания, что убывает экспоненциально от расстояния страницы р.
Наша модель направлена на подграфы результатов поиска во 2разделе, подчеркивая мотивацию изменения и в противоположном направлении. В дополнение к тому, на что ссылается страница р, что бы увеличить наше понимание ее содержания, мы неявно используем текст на страницах, которые ссылаются на р (ибо если страницы в корневом наборе для «поисковых машин» ссылаются на yahoo.com, то мы включим yahoo.com в наш подграф). Это понятие имеет отношение к поиску, основанном на текстах ссылок, в котором рассматривается окружающий текст гиперссылки как ключевое слово страницы, которое указывает на значимость этой страницы. Использование текста ссылок появилось в одной из старейших поисковых машинах McBryan’s World Wide Worm Web-[40]; что также использовалось в работах [8, 11, 10].
Еще одним направлением работы по интеграции ссылок при веб-поиске является создание поисковых формализмов, способных обрабатывать запросы, связанные с предикатами как текстов, так и ссылок. Аросена, Мендельсон и Миаила [1] разработали концепцию поддержки веб-запросов, которые сочетают в себе стандартные ключевые слова с условиями в окружающей ссылочной структуре.
Группирование ссылочных структур в контексте библиометрии, гипертекста и сети было сосредоточено в основном на проблеме разложения множества узлов в «сплоченные» подмножества. В основном это применялось к незначительным множествам объектов, например, уделялось внимание сборникам научных журналов, или множеству страниц одного веб-сайта. Ранее мы указали, в чем принципиальное отличие нашего изучения этого вопроса от тех, которые встречаются в группировках другого рода: наша главная задача состоит в том, чтобы представлять огромное множество страниц в неявном виде, путем создания хабов и авторитетных источников для этого множества. Теперь мы обсудим некоторые предыдущие работы, основанные на цитатах и гипертекстовом группировании, чтобы лучше выяснить его связь с методами, которые мы здесь разрабатываем. В частности, это также будет полезно в 6Разделе, когда мы будем обсуждать методы расчета нескольких множеств хабов и авторитетных источников в рамках одной ссылочной структуры, это можно рассматривать как способ представления нескольких потенциально очень больших неявных группировок.
На очень высоком уровне, группирование требует сходства между объектами и метода группирования по этим сходствам. Двумя основными функциями сходства документов, исходя из библиометрии, являются библиографическая связь (согласно Кесслеру [36]) и совместное цитирование (согласно Смолу [52]). Для пары документов p и q, первыми будут документы, на которые ссылаются p и q, а последними — документы, на которые ссылаются p и q. Совместное цитирование было использовано в качестве измерения сходства веб-страниц, Ларсоном [37], Питковым и Пиролли [47]. Вайс и соавт. [56] определяют измерение сходства на основе ссылок для страниц в гипертекстовой среде, обобщая совместное цитирование и библиографическую связь, для обеспечения сколь угодно длинной цепочки ссылок.
Несколько методов были предложены в этом контексте для формирования групп из множества узлов с некой похожей информацией. Смол и Гриффит [54] используют поиск в ширину для вычисления связанных компонентов неориентированного графа, в котором два узла соединены ребром, тогда и только тогда, когда они имеют положительные значение совместного цитирования. Питков и Пиролли [47] применяют этот алгоритм для изучения ссылочной связи между множеством веб-страниц.
Можно также использовать анализ главных компонент [31, 34] и связанных методов понижения размерности, таких как многомерное шкалирование, для группирования множества узлов. В связи с этим, все начинается с матрицы М, содержащей похожую информацию между парами узлов, и представления (на основе этой матрицы) каждого узла i как высоко-мерного вектора {vi}. Затем используются первые несколько неглавных собственных векторов матрицы подобия М, чтобы определить низко-мерное подпространство, в котором могут быть спроектированы векторы {vi}; различные геометрические или визуальные методики могут использоваться для выявления плотных групп в этом низко-мерном пространстве. Стандартные теоремы линейной алгебры (например, [30]) на самом деле дают однозначные значения, в которых проекция на первый собственный вектор k вызывает минимальные искажения по всей к-мерной проекции данных. Смол [53], Маккейн [41] и др. применили этот метод для журнала и данных совместного цитирования авторов. Применение методов понижения размерности в группировании веб-страниц на основе совместного цитирования было использовано Ларсоном [37], Питковым и Пиролли [47].
Группирование документов или страниц с гиперссылками, конечно, может быть обусловлено комбинациями текстовой и ссылочной информации. Такие комбинированные измерения были изучены Шоу [50, 51] в контексте библиометрии. Совсем недавно Пиролли, Питков и Рао [46] использовали комбинацию ссылочной топологии и текстового сходства, чтобы сгруппировать и классифицировать веб-страницы.
Наконец, мы обсудим два других метода группирования, основанных на собственных векторах, которые были применены к ссылочной структуре. Сфера спектрального разбиения графа была начата работами Доната, Хоффмана [18] и Фидлера [23]; см. последнюю книгу Чанга [12] для обзора. Методы спектрального разбиения графа устанавливают соотношения между слабосвязанными частями неориентированного графа G в собственных значениях и собственными векторами их матрицы инцидентности A. Каждый собственный вектор А имеет одну координату для каждого узла G, и, следовательно, может рассматриваться как распределение весов узлов G. Каждый неглавный собственный вектор имеет как положительные, так и отрицательные координаты; одной из фундаментальных эвристических процедур, вытекающей из исследования этих спектральных методов, является то, что узлы, которые соответствуют положительным координатам с большим значением, заданным собственным вектором, как правило, очень редко связаны с узлами, которые соответствуют отрицательным координатам с большим значением одного и того же собственного вектора.
С другой стороны, центроидное шкалирование является методом группирования, предназначенным для представления двух типов объектов в общем пространстве [38]. Рассмотрим, например, множество людей, которые ответили на анкетные вопросы. Можно представить людей и возможные ответы в общем пространстве, в некотором смысле так, что каждый человек является «приближенным» к ответам, которые он или она выбрали, и каждый ответ является «приближенным» к людям, которые выбрали его. Центроидное шкалирование обеспечивает метод, основанный на собственном векторе, для этого осуществления. Данная формулировка похожа на наш метод определения хабов и авторитетных страниц, в котором использовался метод собственных векторов для создания соответствующих множеств весов для двух различных типов объектов. Принципиальное различие, однако, состоит в том, что метод центроидного шкалирования, как правило, не связан с интерпретацией только координаты с большим значением в проведенной выборке; скорее, целью является ввести понятие сходства между набором объектов при помощи среднего геометрического значения. Центроидное шкалирование было применено Нома к цитированным данным [43], для совместного группирования цитирований и цитируемых документов. В контексте поиска информации, метод скрытого семантического индексирования по Дирвестеру и соавт. [16] применял метод центроидного шкалирования для модели векторного пространства документов [48, 49]. Это позволяет им представлять условия и документы в общем низко-мерном пространстве, в котором геометрическое группирование часто разделяет множественные значения термина запроса.
Алгоритм, представленный в 3 разделе, в некотором смысле, является поиском наиболее плотно связанных наборов хабов и авторитетных источников в подграфе Gσ, который определен строкой запроса σ. Однако, существует ряд наборов, в которых может быть интересным поиск нескольких плотно связанных множеств хабов и авторитетных источников между тем же набором страниц Sσ. Каждый такой набор потенциально может иметь отношение к теме запроса, но они легко могут быть отделены друг от друга в графе Gσ по целому ряду причин. Например,
В каждом из этих примеров, релевантные документы могут быть объединены в несколько групп. Проблема при запросах на обширную тему, однако, состоит не только в том, что бы достичь разделения умеренных групп, надо также иметь дело с проблемой избытка. Каждая группа, в контексте целого веба, является огромной, и поэтому нам необходим способ извлечь небольшой набор хабов и авторитетных источников из каждой из них. Таким образом, можно рассматривать такие наборы хабов и авторитетных источников как однозначное представление выдержки для обширной темы из набора больших групп, которые мы никогда однозначно не представляли. На очень высоком уровне, наша мотивация в этом смысле аналогична технике поиска информации, такой как Скейтера/Гейзера [14], которые стремятся представить очень большие группы документов через методы, основанные на текстах.
В 3 разделе, мы вычислили хабы и авторитетные источники по главным собственным векторам матриц ATA и AAT, где А является матрицей инцидентности Gσ. Неглавные собственные векторы ATA и AAT предоставляют нам естественный способ извлечения дополнительных плотно связанных наборов хабов и авторитетных источников из базового набора Sσ. Прежде всего отметим следующие основные факты.
Предположение 6.1. ATA и AAT имеют одинаковое мультимножество с собственными значениями, и их собственные векторы могут быть выбраны так, чтобы ωi(AAT)=Aωi(ATA).
Таким образом, каждая пара собственных векторов xi∗ = ωi(ATA), yi∗ = ωi(AAT), связанная как в предположении 6.1, имеет следующие свойства: применение I операции к (xi∗, yi∗) удерживает х-веса параллельно к xi∗, и применение O операции к (xi∗, yi∗) удерживает у-веса параллельно к yi∗. Таким образом, каждая пара весов (xi∗, yi∗) имеет точную взаимоусиляющую связь, к который мы стремимся в паре хаб/авторитетный источник. Кроме того, применение I•O (соответственно O • I) увеличивает значение xi∗ (соответственно yi∗) с коэффициентом |λi|; поэтому |λi| дает точную степень взаимного усиления весов хабов yi∗ и весов авторитетных источников xi∗.
Теперь, в отличие от главного собственного вектора, неглавные собственные вектора имеют как положительные, так и отрицательные элементы. Следовательно, каждая пара (xi∗, yi∗) обеспечивает нас двумя плотно связанными наборами хабов и авторитетных источников: те страницы, которые соответствуют с-координатами с наиболее положительными значениями, и те страницы, которые соответствуют с-координатам с наиболее отрицательными значениями. Эти наборы хабов и авторитетных источников имеют одинаковый интуитивный смысл, приведенный в 3 разделе, хотя алгоритм их поиска, основанный на неглавных собственных векторах, по идее является менее «чистым» чем метод итераций I и O операции. Отметим также, что поскольку степень, с которой веса в xi∗ и yi∗ усиливают друг друга, хабов и авторитетных источников, связанных с собственными векторами, выше абсолютной величины, и как правило, будет «плотнее», как у подграфов в ссылочной структуре и, следовательно, будет часто иметь более интуитивный смысл.
В 5 разделе мы рассмотрели, что спектральные эвристические процедуры разделения неориентированных графов [12, 18, 23] указывали на то, что узлы с большими положительными координатами в неглавных собственных векторах часто хорошо отделяются от узлов с большими отрицательными координатами в тех же собственных векторах. Согласно нашему контекст, который занимается неориентированными, а не неориентированными графами, можно задаться вопросом: есть ли естественное «разделение» между этими двумя наборами авторитетных источников, связанных с тем же неглавным собственным вектором. Мы увидим, что в некоторых случаях существует различие между этими двумя наборами, в том смысле, что касается темы запроса. Стоит отметить, что значения координат в любом неглавном собственном векторе представляют собой чисто условное решение следующих симметрий: если xi∗ и yi∗ являются собственными векторами, связанными с λi, то получаем − xi∗ и − yi∗.
Основные результаты. Приведем теперь некоторые примеры того, каким образом применение неглавных собственных векторов приводит к созданию многократных наборов хабов и авторитетных источников. Возникает следующее интересное явление. Страницы с большими значениями координат в первых нескольких неглавных собственных векторах будут повторяться, так что по существу тот же набор хабов и авторитетных источников будет часто образовываться за счет нескольких сильнейших неглавных собственных векторов. (Несмотря на то, что они имеют похожие большие значения координат, эти собственные векторы остаются ортогональными благодаря различиям в меньших абсолютных значениях координат). Таким образом, получается меньшее количество определенных наборов хабов и авторитетных источников, чем можно было бы ожидать от множества неглавных собственных векторов. Это понятие также отражено в приведенном ниже примере, где мы выбрали (вручную) несколько определенных наборов из числа первых неглавных собственных векторов.
Мы задаем первый запрос, как «ягуар*», просто как один из способов поиска самого слова или его множественного числа. Для этого запроса наиболее стойкие наборы авторитетных источников касаются продукции Atari Jaguar, НФЛ футбольной команды из Джэксонвилля, и автомобиля.



По запросу «рандомизированные алгоритмы», ни один из наиболее стойких наборов хабов и авторитетных страниц не соответствуют в точности теме запроса, хотя все они состоят из тематически связанных страниц тесно связанной темы. Они включали в себя домашние страницы ученых-теоретиков в области компьютерных наук, сборники математического программного обеспечения и страницы по вейвлет-преобразованию.



Мы также сталкиваемся с примерами, где страницы с положительными и отрицательными концами тех же неглавных собственных векторов изображают естественное разделение. Единственный случай, в котором значение этого разделения особенно заметно, проявляется при запросе «аборт». Возникает естественный вопрос, производит ли один из неглавных собственных векторов разделение между авторитетными источниками сторонников и противников. Вопрос осложняется существованием хабов, активно ссылающихся на страницы обеих сторон, но на самом деле 2-й неглавных собственный вектор дает очень четкое разделение:


Вернемся к методу 3 раздела, в котором мы определили разовый набор хабов и авторитетных страниц в подграфе Gσ, связанный со строкой запроса σ. Алгоритм вычисляет плотно связанный набор страниц, независимо от их содержания; дело в том, что эти страницы, имеющие отношение к теме запроса, часто основаны на том, как мы построили подграф Gσ, убедившись, что он содержит много релевантных страниц. Можно рассмотреть этот вопрос следующим образом: многие различные темы, представленные в Gσ, и каждая из них сосредоточена вокруг альтернативного набора плотно связанных хабов и авторитетных страниц. Наш способ получения целенаправленного подграфа Gσ направлен на заверение того, чтобы наиболее важные наборы такие же «наиболее плотные», и, следовательно, будут сгенерированы при итерации I и O операций.
Когда начальная строка запроса σ определяет тему, которая не является достаточно широкой, однако, часто не имеет достаточное количество релевантных страниц в Gσ, из которого извлекается достаточно плотный подграф соответствующих хабов и авторитетных страниц. В результате, авторитетные страницы, соответствующие альтернативным «широким» темам, будут иметь преимущество над страницами, имеющим отношение к σ, и будут возвращены с помощью алгоритма. В таких случаях мы говорим, что этот процесс распределяется от первоначального запроса.
Хотя это ограничивает возможности нашего алгоритма в порске авторитетных страниц для узких или конкретных тем запроса, распределение может быть интересным процессом. В частности, широкая тема, которая заменяет оригинальный и достаточно конкретный запрос σ, очень часто представляет собой естественное обобщение σ. Как таковое, это обеспечивает простой способ абстрагирования определенной темы запроса от более широкой и связанной.
Рассмотрим, например, запрос «Интернет-конференции». В то время как мы повторили этот запрос, AltaVista выдала примерно 300 страниц, содержащих строку; однако конечный подграф Gσ, содержащий страницы, связанные с хостом общих веб-тем, и главные авторитетные страницы на самом деле оказались общими веб-ресурсами.

В контексте запросов подобных страниц, запрос типа «слишком специфический» примерно соответствует странице р, которое не имеет достаточно высокой входящей степени. В таких случаях процесс распределения может также обеспечить уточнение обширной темы более значимых страниц, связанных с р. Рассмотрим, например, результаты, когда р — sigact.acm.org, главная страница ACM специальной группы по теории алгоритмов и вычисления, которая сосредотачивается на теоретической информатике.

Проблема поиска более конкретных ответов является предметом текущей работы; в 8 и 9 разделах, мы кратко обсудим текущую работу по использованию текстового контента с целью сосредоточения нашего подхода к анализу ссылок [6, 10, 11]. Использование неглавных собственных векторов в сочетании с основным термином соответствия может быть простым способом извлечения наборов авторитетных страниц, которые более релевантные для конкретной темы запроса. Например, рассмотрим следующий факт: среди множества хабов и авторитетных страниц, которые соответствуют первым 20 неглавным собственным векторам, в котором страницы совместно содержат строку » Интернет-конференции», следующие:

Оценка методов, представленных здесь, является сложной задачей. Прежде всего, конечно, мы пытаемся определить и вычислить меру «авторитетности», которая по своей сути основана на человеческих суждениях. Кроме того, сущность интернета усложняет задачу оценки — это новый домен, с отсутствием стандартных критериев; разнообразие стилей авторитетных страниц намного большее, чем у аналогичных сборников опубликованных документов. Интернет является очень динамичным, с часто обновляемым новым материалом и без подробного индекса полного содержания.
В предыдущих разделах статьи мы привели ряд примеров, исходящих из нашего алгоритма. Это было сделано, чтобы показать читателю полученные результаты, и потому, что мы считаем, что есть неизбежный компонент, говорящий сам по себе об общей оценке. Наши ощущения дают весьма яркий результат весьма на очевидном уровне.
Однако есть и более принципиальные способы оценки алгоритма. С момента появления опубликованного варианта этого документа, три различных исследования, которые проводились при помощи двух различных групп [6, 10, 11], помогли оценить стоимость нашего метода в контексте инструмента для поиска информации на интернете. Каждое из этих исследований использовало системы, основанные в основном на описанном здесь алгоритме, для размещения хабов и авторитетных страниц в подграф Gσ с помощью методов, описанных в 2 и 3 разделах. Тем не менее, каждая из этих систем также использовала дополнительные эвристические процедуры для дальнейшего повышения значимости суждения. Самое главное то, что они включали измерения на основе текста, такие как оценка текста ссылки для дифференцированного взвешивания вклада отдельных ссылок. Таким образом, результаты этих исследований не должно быть истолкованы как предоставление прямой оценки чисто ссылочного метода, описанного здесь, скорее, они оценивают его работу в качестве основного компонента инструмента веб-поиска.
Мы кратко рассмотрим структуру и результаты последние из этих трех исследований, включая систему Clever, разработанную Чакрабарти и соавт. [10]. Для более подробной информации ознакомьтесь с указанной работой. Основная задача в этом исследовании состояла в автоматической компиляции источников (структура списков высококачественных веб-страниц, связанных с обширной темой поиска) и целью было увидеть результат для набора из 26 тем от Clever и сравнить со списком, скомпилированным вручную при помощи таких систем как поисковый сервис Yahoo! [58].
Таким образом, результатом Clever для каждой темы был список из десяти страниц: пятерка «лидеров» хабов и пятерка «лидеров» авторитетных страниц. Yahoo! была использована в качестве основной точки сравнения, так как ее списки, сгенерированные вручную, можно рассматривать как эквивалент суждения «авторитетности» людей, которые компилировали их. Были выбраны первые десять страниц, найдены при помощи AltaVista, так чтобы получить репрезентативные страницы, полностью сгенерированные при помощи автоматических текстовых поисковых систем. Все эти страницы были собраны в единый список тем для каждой темы в исследовании, без указания того, какой метод использовался для каждой страницы. Был собран набор из 37 пользователей; пользователи должны были быть знакомы с использованием веб-браузера, но не должны были быть экспертами в области компьютерных наук или в 26 темах поиска. Затем пользователей попросили ранжировать страницы из списка тем, которые они посетили, как «плохие», «удовлетворительные», «хорошие» или «отличные» с точки зрения их полезности в изучении этой темы. Это дало 1369 ответов, которые затем были использованы для оценки относительного качества Clever, Yahoo! и AltaVista по каждой теме. Для, примерно, 31% тем оценки Yahoo! и Clever были эквивалентны и находились в пределах порога статистической значимости; примерно 50% оценивали выше Clever; а оставшиеся 19% оценивали выше Yahoo!.
Конечно, трудно делать окончательные выводы из этих исследований. Службы, такие как Yahoo!, действительно, по своей природе предусматривают тип человеческого суждения о том, какие страницы являются «хорошими» для конкретной темы. Но даже характер качества оценки, конечно, не очень хорошо определен. Кроме того, многие данные в Yahoo! взяты из внешних ссылок и, следовательно, представляют собой менее непосредственное «авторитетное» суждение сотрудников Yahoo!.
Многие пользователи в этих исследованиях сообщали, что они использовали списки в качестве отправной точки изучения, но они побывали на многих страницах, которые не находились в оригинальных списках тем, созданными различными методами. Это, конечно, естественный процесс в исследовании широкой темы в интернете, и цель списка источников состоит в облегчении этого процесса, а не его замены.
Мы обсудили методы локализации высококачественной информации, связанной с широкой темой поиска в Интернете, основанные на структурном анализе топологии ссылок «авторитетных» страниц этой темы. Можно выделить четыре основные составляющие нашего метода.
Для широких тем в Интернете, количество соответствующей информации растет очень быстро, что утрудняет для отдельных пользователей фильтрацию доступных ресурсов. Чтобы справиться с этой проблемой, необходимо ввести понятия релевантности и группирования. Необходимо профильтровать широкую тему запроса, в которой могут находиться миллионы релевантных страниц, вплоть до представления ее в достаточно компактном виде. Именно для этой цели мы ввели понятие «авторитетные» источники, основанное на структуре ссылок веба.
Мы заинтересованы в получении наиболее качественных результатов из доступной по всему вебу информации. Наш основной домен не ограничивается целевым набором страниц, или теми, кто постоянно посещает один и тот же веб-сайт.
В то же время, мы делаем вывод о глобальном понятии структуры без непосредственного использования веб-индекса или ссылочной структуры Интернета. Нам необходимы только базовый интерфейс для любого количества стандартных веб-поисковых систем и методы получения «улучшенных» образцов веб-страниц для определения понятия структуры и качества, которые имеют смысл в глобальном масштабе. Это помогает решить проблемы работы с темами, которые имеют огромное представление в Интернете.
Нашей первоначальной целью был обнаружение авторитетных страниц, но наш подход на самом деле идентифицирует более сложную картину общественной организации сети, в которой хабы плотно ссылаются на набор тематически связанных авторитетных страниц. Это равновесие между хабами и авторитетными станицами – это явление, которое повторяется в контексте широкого круга вопросов в сети. Измерение эффективности и влиятельности в библиометрии, как правило, не полноценное и имеет аналогичное формулирование роли, которую выполняют хабы; Интернет очень отличается от научной литературы, и наша основа представляется целесообразным в качестве модели отображения авторитетных страниц в среде, такой как Интернет.
Эта работа была дополнена несколькими способами с момента первого доклада на конференции. В 8 разделе мы упоминали о системах для компиляции списков высококачественных веб-ресурсов, которые были созданы с использованием расширений разработанных здесь алгоритмов (см. Барат и Хенцингер и др. [6] и Чакрабарти [10, 11]). Реализация системы Барат-Хенцингера использовала недавно разработанную Connectivity Server (Барат с соавт. [5]), которая обеспечивает довольно эффективный поиск для связанной информации, содержащейся в индексе AltaVista.
С Гибсоном и Рагхаваном, мы использовали алгоритмы, описанные здесь, чтобы изучить структуру «объединений» хабов и авторитетных страниц в сети [28]. Мы считаем, что понятие обобщения темы, которое обсуждалось в 7 разделе, обеспечивает единую точку зрения, которая находит точки пересечения таких «объединений». В другом направлении, также с Гибсоном и Рагхаваном, мы исследовали развитие настоящей работы для анализа связанных данных, и рассмотрели естественный нелинейный аналог спектральных эвристических процедур для этой ситуации [29].
Много интересных дальнейших направлений появились в связи с этими исследованиями, в дополнение к упомянутым выше. Мы ограничимся здесь лишь тремя такими направлениями.
Во-первых, мы использовали структурную информацию о графе, определенную веб-ссылками, но мы не использовали особенности их трафика и путей, по которым пользователи неявно переходят в этом графе, и как они посещают последовательность страниц. Есть целый ряд интересных и фундаментальных вопросов, которые можно задать о веб-трафике, включая моделирование такого трафика и разработку алгоритмов и инструментов для использования информации, полученной от трафика (см., например, [2, 3, 33]). Было бы интересно узнать, как разработанный подход может быть интегрирован в изучение множества пользовательского трафика в сети.
Во-вторых, мощность эвристических процедур, основанных на собственных векторах, не до конца понятная на аналитическом уровне, и было бы интересно заниматься этим вопросом в контексте алгоритмов, представленных здесь. Одно из направлений сконцентрировано на рассмотрение случайных моделей графа, которые содержат достаточную структуру для охвата определенных глобальных свойств веб-сети, и все же достаточно просты, чтобы можно было проанализировать их с помощью наших алгоритмов. В более общем плане разработка достаточно точной случайной модели графа для веб-сети может быть чрезвычайно ценной для понимания ряда алгоритмов, основанных на ссылках. Некоторые работы этого типа были проведены в контексте метода латентно-семантический анализа поиска информации [16]: Пападимитриу с соавт. [44] предоставили теоретическое применение латентно-семантического анализа для основных статистических моделей использования терминов в документах. Другое направление, частично мотивированное в нашей работе. Фриз, Каннан и Вемпала проанализировали довольно эффективную методологию выборки в соответствии с аппроксимацией сингулярного разложения большой матрицы [24]. Понимание конкретных связей между их работой и нашей методикой выборки во 2 разделе было бы весьма интересно.
И наконец, дальнейшее развитие методов, основанных на ссылках для обработки информационных потребностей, кроме запросов обширных тем в веб-сети, ставит много интересных задач. Как отмечалось выше, работа была проделана по включению текстового содержания в нашу схему как способа «конкретизации» обширных тем поиска [6, 10, 11], но можно задаться вопросом, что другие основные информационные структуры могут выделить, кроме хабов и авторитетных страниц, из топологии ссылок гипермедиа, таких как веб-сеть. Средства, с помощью которых взаимодействие со ссылочной структурой может способствовать изучению информации, являются общим и далеко идущим понятием, и нам кажется, что оно будет продолжать предлагать ряд интересных алгоритмических возможностей.
На ранних этапах работы, я премного благодарен за дискуссии Прабхакару Рагхавану и Роберту Клайнбергу; я признателен Сумену Чакрабарти, Бирону Дому, Девиду Гибсону, С. Равви Кумару, Прабхакару Рагхавану, Сридхару Раджагопалану и Эндрю Томкинсу для совместную работу по расширению и улучшению этой работы; и я благодарю Ракешу Агравалу, Тригу Агеру, Робу Баретту, Маршаллу Берну, Тиму Бернер-Ли, Ашоку Чандару, Монике Хенцигер, Алану Хоффману, Девид Каргер, Лилиану Ли, Нимроду Мегиддо, Кристосу Пападимитриу, Питеру Пиролли, Теду Селкеру, Эли Упфалу и анонимным рецензентам этой работы за их ценные замечания и предложения.
Перевод материала «Authoritative Sources in a Hyperlinked Environment» выполнил Сергей Неиленко
Полезная информация по продвижению сайтов:
Перейти ко всей информации