SEO-Константа
Яндекс.Директ + оптимизация
Граф веб-ссылок имеет вложенные компоненты двусвязаности: подавляющее большинство гиперссылок связывают страницы на хосте с другими страницами того же хоста, но многие из них не связывают страницы в пределах одного домена. Мы покажем, как можно использовать эту связь, чтобы ускорить вычисления Google PageRank 3-этапным алгоритмом при котором (1) локальный PageRank страниц для каждого хоста рассчитываются независимо, используя связь ссылок этого хоста, (2) эти локальные PageRank затем анализируются касательно «важности» соответствующего хоста, и (3) затем выполняется стандартный алгоритма PageRank с использованием, в качестве исходного вектора, взвешенной сети локального PageRank. Эмпирически, этот алгоритм в реальных условиях ускоряет вычисления PageRank в 2 раза. Кроме того, мы разрабатываем вариант данного алгоритма, который эффективно вычисляет множество различных «персонализированных» PageRank, и вариант, который эффективно пересчитывает PageRank после обновлений узла.
Быстро растущий веб-граф содержит несколько миллиардов узлов, что делает вычисления на графах очень дорогим. Один из самых известных вычисления на графах — Google PageRank, алгоритм определения «важности» веб-страниц [14]. В основу алгоритма Google PageRank положена многократная итерация связей веб-графа до получения стабильного значения важности страницы. Так как это вычисление может занять несколько дней на веб-графах с несколько миллиардами узлов, разработка методов для снижения вычислительной сложности алгоритма становится необходимым по двум причинам. Во-первых, ускорение этого вычисления является частью общей эффективности, необходимой для получения актуального значения данных веб-индекса. Во-вторых, современные подходы к схемам персонализированного и Topic-sensitive PageRank [8, 10, 16] требуют вычисления комбинации векторов PageRank, вызывая острую необходимость в более быстрых методах вычисления PageRank.
Предыдущие подходы к ускорению вычислений PageRank использовали общие методы разряженного графа. Arasu и др. [1] чаще используют значения текущей итерации, как только она становится доступной, нежели только значения предыдущей итерации. Также считается, что использование конфигурации веба в «форме бабочки» [3] будет полезным в вычислении PageRank. Тем не менее, этот метод не практикуется, так как упорядочение веб-матрицы в соответствии с его структурой требует поиска в глубину, который является чрезмерно дорогостоящим. Совсем недавно, Kamvar и соавт. [11] предложили использовать последовательные промежуточные итерации, что бы экстраполировать последовательно лучшую оценку истинного значения PageRank. Тем не менее, быстродействие, обозначенное в последних работах, незначительное для задания параметров, которые обычно используются для PageRank. 1
В этой статье предлагается использование подробной типологии веб-графа. Анализ структуры веб-графа сконцентрирован на определении различных свойств графов, таких как степень распределения и связанность статистики, а также на моделировании создания веб-графа [12, 2]. Тем не менее, эти исследования не рассматривают непосредственно, как эта характерная структура может быть эффективно использована для ускорения анализа ссылок. Рагхаван и Гарсиа-Молина [15] использовали имя хоста (или, в общем, URL)-индуцированную структуру веба, что бы эффективно представить веб-граф. В этой статье мы непосредственно рассматриваем использование этого вида структуры для достижения большего ускорения по сравнению с предшествующими алгоритмами для вычисления PageRank, путем:
В следующих разделах мы исследуем структуру веба, рассматривая алгоритм вычисления PageRank, и обсудим ускорение этого алгоритма, которое достигается на массиве реальных данных. Наша экспериментальная модель описана далее. Для наших экспериментов мы использовали два массива данных различной величины. Граф ссылок STANFORD/BERKELEY был создан из поиска доменов stanford.edu и berkeley.edu, созданных в декабре 2002 года в рамках Стэнфордского проекта WebBase. Этот граф ссылок (после удаления висячего узла, см. ниже) содержит около 683500 узлов, с 7,6 миллионами ссылок, и требует 25Мб памяти. Мы использовали STANFORD/BERKELEY при разработке алгоритмов, чтобы понять их действие. Для практической оценки эффективности мы используем граф ссылок LARGEWEB, полученный из поиска Web, который был создан в январе 2001 года в рамках Стэнфордского проекта WebBase [9]. Полная версия этого графа, называемая FULL-LARGEWEB, содержит примерно 290 миллионов узлов, чуть более миллиарда ребер, и требует 6 ГБ памяти. Многие из этих узлов – висячие узлы (страницы без исходящей связи), либо потому, что страницы действительно не имеют исходящей связи, или потому, что это страницы, которые были открыты, но не были добавлены в поиск. При расчете PageRank, эти узлы будут исключены из веб-графа до нескольких последних итераций, поэтому мы также рассматриваем версию LARGEWEB с удалением висячих узлов, так называемая DNR-LARGEWEB, которая содержит примерно 70 миллионов узлов, с более чем 600 млн. ребер, и требует 3,6 ГБ памяти. Графы ссылок хранятся с использованием отображения списка смежных ребер вместе с отображением страниц в виде идентификатора 4-байтовых целых чисел. На машине AMD Athlon 1533MHz с 6- way RAID-5 томным диском и 3,5 Гб оперативной памяти, каждая итерация PageRank массива данных на 70 миллионах страниц DNR-LARGEWEB занимает примерно 7 минут. Учитывая, что для вычисления Google PageRank обычно необходимо до 100 итераций, актуальной является потребность в быстрых вычислительных методах для больших графов. Наш критерий для определения сходимости следующих алгоритмов использует L1 норму вектора невязок, т. е. ||Ax→(k) — x→(k)||1. Мы отсылаем читателя к [11] для обсуждения, почему невязка L1 является надлежащей мерой для измерения сходимости.
Основные термины, которые мы используем далее в обсуждении, приведены в Таблице 1.
| Термин | Пример cs.stanford.edu/research/ |
| Домен верхнего уровня | edu |
| Домен | stanford.edu |
| Имя хоста | cs |
| Хост | cs.stanford.edu |
| Путь | /research/ |
Таблица 1 Пример, иллюстрирующий нашу терминологию с использованием образца URL cs.stanford.edu/research/
Для исследования структуры веба, мы провели следующий простой эксперимент. Мы охватили все гиперссылки FULL-LARGEWEB, и посчитали, сколько из этих ссылок являются «внутрихостовыми» (ссылки с одной страницы на другую в том же хосте) и сколько «межхостовыми» (ссылки со одной страницы на другую в другом хосте). Таблица 2 показывает, что 79,1% ссылок в этом массиве данных являются внутрихостовыми ссылками, а 20,9% — межхостовые ссылки. Эта статистика связанности внутрихостовых ссылок не далека от более ранних результатов Bharat соавт. [2]. Мы также исследовать количество внутридоменных и междоменных ссылок. Обратите внимание в таблице 2, что большинство ссылок являются внутридоменными (83,9%).
| Домены | Хост | |
| Full Intra | 953 миллиона ссылок (83,9%) | 899 миллиона ссылок (79,1%) |
| Full Inter | 183 миллиона ссылок (16,1%) | 237 миллиона ссылок (20,9%) |
| DNR Intra | 578 миллиона ссылок (95,2%) | 568 миллиона ссылок (93,6%) |
| DNR Inter | 29 миллиона ссылок (4,8 %) | 39 миллиона ссылок (6,4%) |
Таблица 2 Статистика гиперссылок на LARGEWEB для полного графа (Full: 291 миллионов узлов, 1.137 миллиардом ссылок) и для графа с удалением висячих узлов (DNR: 64.7 миллионов узлов, 607 миллионов ссылок)
Эти результаты интуитивно очевидны. Возьмем в качестве примера домен cs.stanford.edu. Большинство из ссылок в cs.stanford.edu являются ссылками сайта cs.stanford.edu (например, cs.stanford.edu/admissions, или cs.stanford.edu/research). Кроме того, почти все не навигационные ссылки – это ссылки на другие хосты Stanford, такие как www.stanford.edu, library.stanford.edu или WWW-CS-students.stanford.edu. Как ожидается, существует эта структура даже в более низких уровнях иерархической структуры веба. Например, можно ожидать, что страницы cs.stanford.edu/admissions/ тесно взаимосвязаны между собой, и очень слабо связаны со страницами в других подуровнях, что приводит к вложенным компонентам двусвязаности. Этот тип вложенных компонентов двусвязаности может быть обнаружен путем сортирования графа ссылок, что бы построить матрицу ссылок следующим образом. Мы сортируем URL лексикографически, за исключением того, что в качестве ключа сортировки мы реверсируем компоненты домена. Например, ключом сортировки для URL www.stanford.edu/home/students/ будет edu.stanford.www/home/students. При построении матрицы ссылок URL присваиваются последовательные идентификаторы. Матрица ссылок содержит в качестве элементов (i,j) — 1, если есть ссылка от i до j, или 0 в противном случае. URL можно сгруппировать в свою очередь по домену верхнего уровня, домену, хосту, и, наконец, по пути. Подграф страниц в stanford.edu выступает в качестве субблока матрицы целостных ссылок. В свою очередь, подграф для страниц WWW-db.stanford.edu выступает в качестве вложенного субблока.
Мы можем затем получить сведение о структуре веба с помощью точечных диаграмм для визуализации матрицы ссылок. Если существует ссылка со страницы i на страницу j, то точка (i,j) изображается на точечной диаграмме цветной, в противном случае точка (i,j) – белая. Если наш массив данных являются слишком большим, чтобы различить отдельные пиксели, мы рассматриваем несколько фрагментов веба (Рис.1). Обратите внимание на три вещи:
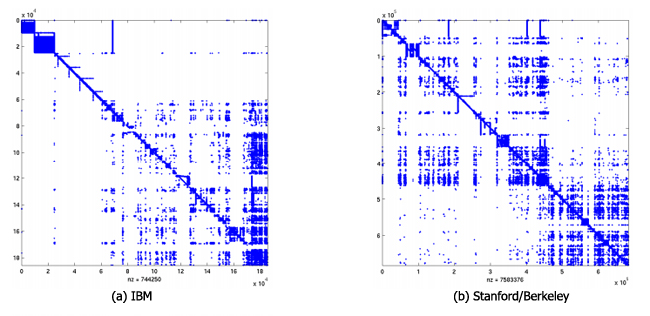
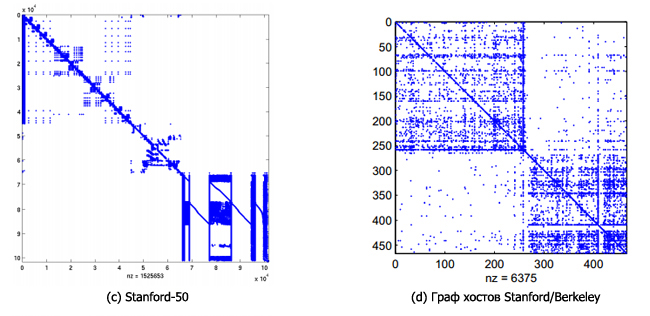
Рис. 1: Вид 4 разных фрагментов веба: (a) домен, (b) все хосты в доменах Stanford и Berkeley, (c) первые 50 доменов Stanford, по алфавиту, и (d) хост-граф доменов Stanford и Berkeley.
На рисунке 1 (а) показана точечная диаграмма для домена ibm.com. Обратите внимание, что существуют отчетливые компоненты, которые соответствуют различным хостам ibm.com, например, верхний левый блок соответствует хостам almaden.ibm.com (хосты для IBM Almaden Research Center). Обратите внимание, что страницы в самом конце диаграммы (страницы i ≥ 18544) имеют значительную входящую связь (вертикальные линии в нижнем правом углу диаграммы). Эти страницы относятся к хосту www.ibm.com, и считается, что они будут иметь значительную входящую связь. Также обратите внимание, что есть 4 модели, которые выглядят как перевернутая буква «L». Эти сайты, которые имеют неглубокую иерархию; корневой узел связывает большинство страниц в хосте (горизонтальные линии) и связан с большинством страниц в хосте (вертикальная линия), но взаимосвязей внутри самого сайта не так уж и много (пустой блок). Наконец, заметьте, что область вокруг диагонали очень плотная, что соответствует сильной внутрикомпонентной двусвязаности, особенно в меньших компонентах.
На рисунке 1 (b) показана точечная диаграмма для STANFORD/BERKELEY. Обратите внимание, что она также имеет вполне определенную связанность компонентов и плотную диагональ. Кроме того, эта диаграмма проясняет вложенные компоненты двусвязаности веба. Суперблок на верхней левой стороне является доменом stanford.edu, а суперблок на нижней правой части является доменом berkeley.edu. На рисунке 1 (с) крупным планом изображены первые 50 хостов в алфавитном порядке домена stanford.edu. Большая часть этой диаграммы состоит из 3 крупных хостов: acomp.stanford.edu (академических сайте обработки данных в Стэнфорде) в левом верхнем углу; cmgm.stanford.edu (интернет-ресурс биоинформатики) в середине и daily.stanford.edu (веб-сайт Stanford Daily — студенческая газета Стэнфорда) в правом нижнем углу. Есть много интересных структурных мотивов в этой диаграмме. Во-первых, это длинные вертикальные линии в левом верхнем углу. Это соответствует сайту acomp.stanford.edu, большинство страниц в хосте acomp.stanford.edu указывает на этой корневой узел. Кроме того, есть отчетливые вложенные компоненты двусвязаности в acomp.stanford.edu на уровне различных директорий в URL иерархии.
На сайте Stanford Daily можно увидеть диагональные линии, длинные вертикальные блоки, основной блок центре, и короткие тонкие блоки. Первые несколько веб-страниц daily.stanford.edu отображают титульную страницу газеты в течение последних нескольких дней. Каждая титульная страница ссылается на титульную страницу предыдущего выпуска, и поэтому отображается небольшая диагональ в левом верхнем углу блока Stanford Daily. Благодаря URL соглашению об наименованиях Stanford Daily диагонали способствуют лексикографическому упорядочению URL, чтобы упорядочить статьи в хронологическом порядке. Титульные страницы ссылаются на статьи, которые являются средними страницами блока. Таким образом, мы видим, что горизонтальную полосу вверху посередине. Эти статьи имеют обратную ссылку на титульные страницы газет, и поэтому мы видим вертикальные полосы посередине слева. Статьи ссылаются друг на друга, поскольку каждая статья связана с другими статьями той же тематики и того же автора. На это указывает квадратный блок в центре. Длинные вертикальные полосы отображают страницы, которые находятся на стандартном меню каждой страницы сайта (некоторые страницы этого меню являются страницами «Подписки», «Отправьте сообщение редактору» и «Объявления»). Наконец, диагональные линии, которые окружают середину блока, являются страницами, такими как «Отправьте эту статью другу на e-mail» или «Оставить комментарий к этой статье», которые связаны только с одной статьей.
Рисунок 1 (d) изображает гиперграф доменов stanford.edu и berkeley.edu, в которых каждый хост рассматривается как единый узел, а ребра помещаются между хостами i и j, если есть связь между любой страницей в хостах i и j. Опять же, мы наблюдаем прочную структуру компонентов на уровне домена, и плотная диагональ указывает также на прочную структуру компонентов на уровне хоста. Вертикальные и горизонтальные линии возле нижнего ребра правой части доменов Stanford и Berkeley представляют собой хосты www.stanford.edu и www.berkeley.edu, как и ожидалось, эти хосты тесно связаны с большинством других хостов в пределах их собственного домена.
Мы исследуем здесь размеры хостов в сети. Рисунок 2 (а) показывает распределение числа (поисковых) страниц хостов в LARGEWEB. Обратите внимание, что большинство сайтов — небольшие, порядка 100 страниц. Рисунок 2 (б) показывает размеры компонентов хоста в сети, когда удаляются подвисшие узлы. При удалении подвисших узлов, компоненты становятся меньше, а распределение по-прежнему смещается в сторону небольших компонентов. Крупнейших компонент имел 6000 страниц. В следующих разделах мы увидим, как использовать небольшие размеры компонентов, по отношению к массиву данных в целом, для ускорения анализа связи ссылок.
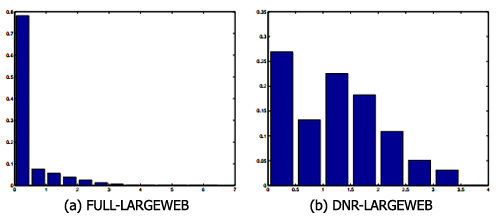
Рис.2. Гистограмма распределения хоста в сети по размерам. Оси х характеризирует размер области памяти для log10 размера компонентов хоста, а ось у — долю компонентов хоста того же размера.
Можно было бы ожидать, что большинство доменов имеют высокую внутригрупповую плотность связи ссылок, как и в cs.stanford.edu, но есть некоторые домены, которые, как предполагается, имеют низкую внутригрупповую плотность связи ссылок, например pages.yahoo.com (ранее называвшийся www.geocities.com). Веб-сайт pages.yahoo.com является корневой страницей Yahoo! GeoCities, бесплатной услугой Веб-хостинга. Нет никаких оснований предполагать, что люди, которые имеют веб-сайты на GeoCities, предпочитают внутренние, а не внешние ссылки GeoCities. 2 На рисунке 3 показана гистограмма внутридоменной плотности сети. На рисунке 3 (а) представлен пик около 0% внутрихостовой связи, характеризирующий, что многие хосты не достаточно взаимосвязаны. Однако когда мы удаляем хосты, которые имеют всего 1 страницу (рис. 3 (b)), этот пик значительно уменьшается, и когда мы исключаем хосты с менее чем 5 страницами, то пик исчезает. Это показывает, что хосты в LARGEWEB, которые не сильно взаимосвязаны, очень малы по размеру. Если удалить очень малые хосты, внутрихостовая плотность большинства хостов становится высокой, и лишь небольшая часть хостов зависит от эффекта GeoCities.
Приведем теперь алгоритм BlockRank, который использует эмпирические результаты из предыдущего раздела, чтобы ускорить вычисления PageRank. Эта работа мотивирована и опирается на методах агрегирования/дезагрегирования [5, 17] и методе разделения областей [6] в численных методах линейной алгебры. 2 и 3 шаги алгоритма BlockRank похожи на метод Релея-Ритца [13]. Мы начнем с обзора PageRank в разделе 4.1.
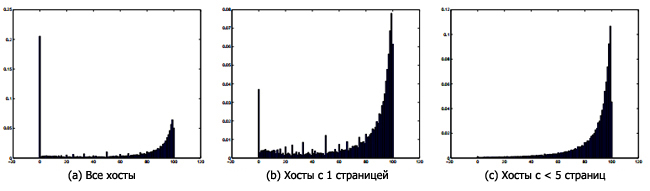
Рисунок 3: Распределение по взаимосвязанности блоков хостов для массива данных DNR-LARGEWEB. X-ось каждого рисунка отображает процентиль памяти для внутрихостовой плотности связи ссылок (процент ребер, которые возникают или завершаются в данном хосте, и находятся во внутрихостовой связи), а Y-ось отображает часть хостов конкретной плотности связи. На рисунке 3 (а) изображено распределение всех хостов во внутрихостовой плотности связи, 3 (б) показывает, то же для хостов, которые имеют более 1 страницы, и 3 (с) показывает, то же для хостов, которые имеют 5 и более страниц.
В этом разделе мы резюмируем определение PageRank [14] и рассмотрим математический аппарат, который будет использоваться нами для анализа и улучшения стандартного итерационного алгоритма для вычисления PageRank. В основе определения PageRank является следующе основное предположение. Ссылки от страниц u ∈ Web к страницам v ∈ Web можно рассматривать как свидетельство того, что v является «важной» страницей. В частности, значение важности приданое v от u пропорционально важности u и обратно пропорциональна количеству страниц u. Поскольку сама важность u неизвестна, определение важности каждой страницы i ∈ Web требует итерационного вычисления с фиксированной запятой.
Для обеспечения более тщательного анализа необходимых вычислений, мы опишем эквивалентную формулировку относительно метода случайного поиска ориентированного веб-графа G. Пусть u → v обозначает существование ребер от u до v в G. Пусть deg(u) будет полустепенью исхода страницы u в G. Рассмотрим случайное пользовательское посещение страницы u в момент к. На следующем интервале времени, пользователь выбирает узел vi из внешних соседних ссылок u в случайном порядке (равномерно). Иными словами, в момент к+1, пользователь находится в узле ui ∈ {u|u → u} с вероятностью 1/deg(u).
PageRank страницы в i определяется как вероятность того, что в какой-то конкретный интервал времени к > K, пользователь находится на странице i. При достаточно больших K, и с незначительными изменениями случайного поиска, эта вероятность является особенной, как проиллюстрировано ниже. Рассмотрим цепь Маркова вызванную случайным поиском G, где состояния задаются узлами в G, и вероятностной матрицей переходов, описывая переход от i к j, который задается P при Pij = 1/deg(i).
Для вероятностной матрицы допустимого перехода, каждый узел для P должен иметь, по крайней мере, 1 исходящий переход, то есть, P не должно иметь строки, состоящие из всех нулей. Это условие выполняется, если G не имеет никаких страниц с полустепенью исхода 0, но оно не относится к веб-графу. P может быть преобразовано в матрицу допустимого перехода, путем добавления полной системы исходящих переходов на страницы с полустепенью исхода 0. Другими словами, мы можем определить новую матрицу Р’, в которой все состояния имеют, по крайней мере, один исходящий переход следующим образом. Пусть n — это число узлов (страниц) в веб-графике. Пусть u→ — это n-мерный вектор столбцов, представляющий равномерное распределение вероятностей по всем узлам:
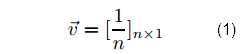
Пусть d→ n-мерный вектор столбцов, определяющий узлы с полустепенью исхода 0:

Затем мы создаем Р’ следующим образом:
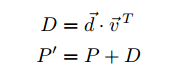
Относительно случайного поиска, эффект от D изменяет вероятности перехода, так что пользователь при посещении висячих страниц (т. е. страниц не имеющих внешних ссылок) случайно переходит на страницу, на следующем интервале времени, используя распределение заданное вектором u→. Согласно эргодической теореме для цепей Маркова [7], цепь Маркова, которая определяется Р’, имеет единственное локальное распределение вероятностей, если Р’ является апериодическим и неприводимым. Это положение справедливо для цепи Маркова касательно веб-графа. Последнее имеет место только в том случае, когда G тесно связана, что, как правило, не относится к веб-графу. В случае вычисления PageRank, стандартным способом обеспечить это свойство является добавление нового массива исходящих переходов с малыми вероятностями перехода для всех узлов, создавая полный (и, следовательно, сильно связный) граф переходов. В матричной форме, мы создадим неразложимую матрицу Маркова Р», следующим образом:
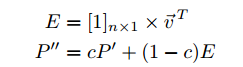
Относительно случайного блуждания, эффект от E следующий. На каждом интервале времени с вероятностью (1-с), пользователь, который посещает любой узел, перейдет к случайной веб-странице (нежели переходя по внешней ссылке). Адрес случайного скачка выбирается в соответствии с распределением вероятностей данной u→. Искусственный переход происходит по причине так называемой операции телепортации E. В работе [14], величина с принималась равной 0,85, и мы используем это значение для всех экспериментов этой работы. Путем повторного определения вектора u→, данного в Уравнении 1 для неоднородности, так что D и E расширяют искусственные переходы с неоднородной вероятностью, результирующий вектор PageRank может быть субъективным, предпочитая определенные виды страниц. По этой причине мы называем u→ вектором персонализации.
Для простоты и согласованности с предыдущей работой, оставшаяся часть обсуждения будет касаться транспонированной матрицы, A = (Р»)T, т. е. распределение вероятностей перехода для пользователя в узел i будет задаваться строкой i для Р», и столбцом i для А. Обратите внимание, что ребра, которые искусственно введены D и E, не нуждаются в явной материализации, поэтому данная конструкция не влияет на эффективность или разреженность матриц, используемых в расчетах. В частности, матрично-векторное умножение y→ = Ax→ может быть реализовано эффективно, используя Алгоритм 1.
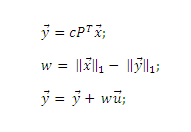
Алгоритм 1. Вычисление y→ = Ax→

Алгоритм 2. Вычисление РageRank
При условии того, что распределение вероятностей расположения пользователя, на момент 0 представляется как x→(0), распределение вероятностей расположения пользователя в момент k представляется как x→(k) = Akx→(0). Уникальное стационарное распределение для цепи Маркова определяется как limk → ∞ х(к), что эквивалентно limk → ∞ Аkх→(0), и не зависит от начального распределения x→(0). Это стационарное распределение является простым главным собственным вектором матрицы A = (P»)T, что является вектором PageRank, который мы хотели бы вычислить. Стандартный алгоритм PageRank вычисляет главный собственный вектор, начиная с равномерного распределения x→(0) = u→ и расчета последовательных итераций x→(k+1) = Ax→(k) до сходимости (то есть, используется степенной метод). Этот алгоритм обобщен в Алгоритме 2. В то время как многие алгоритмы были разработаны для быстрого вычисления собственного вектора, многие из них не подходят для этой задачи из-за размеров и разреженности матрицы Web (см. [11] в обсуждении).
Компоненты двусвязаности веба требуют быстрого алгоритма вычисления PageRank, при котором «вектор локального PageRank» вычисляется для каждого узла, что дает относительную важность страницы в пределах хоста. Эти локальные векторы PageRank затем могут быть использованы
для аппроксимации глобального вектора PageRank, который используется в качестве начального вектора для стандартного вычисления PageRank. Это основная идея алгоритма BlockRank, которую мы резюмируем и излагаем в этом разделе.
Алгоритм выполняется следующим образом:
Этапы мы опишем подробно позже, а некоторые обозначения приведем сейчас. Мы будем использовать знаки нижнего регистра (например, i и j), чтобы представлять показатели отдельных веб-сайтов, и знаки верхнего регистра (I, J), чтобы представлять показатели компонентов. Мы будем использовать сокращенное обозначение i ∈ I, чтобы обозначить ,что страница i ∈ компонент I. Число элементов в компоненте J обозначается nj. Граф данного блока J задается nj х nj субматрицей Gjj матрицы G.
В этом разделе мы рассмотрим вычисление вектора локального PageRank для каждого компонента веба. Так как большинство компонентов слабо взаимосвязаны с внутренними и внешними ссылками блока, по сравнению с общим количеством ссылок блока, кажется правдоподобным, что относительные рейтинги большинства страниц в блоке определяется межблочными связями. Мы определяем вектор локального PageRank l→J блока J (Gjj), что бы применить алгоритм PageRank только для компонента J, будто блок J представляет весь веб, и как если бы ссылки на страницы в других компонентах не существуют. То есть: l→J = pageRank(GJJ, s→J, u→J), где начальный вектор s→J является постоянным вектором вероятности nJ x 1 страниц компонента J ([1/nJ]nx1), а персонализированный вектор u→J — это nJ x 1 вектор, элементы которого одни нули, за исключением элементов, отвечающих за корневой узел компонента J, значение которого 1.
4.3.1. Точность Local PageRank
Чтобы установить, насколько хорошо эти локальные векторы PageRank приближены к относительным величинам истинных векторов PageRank в пределах данного хоста, мы проделаем следующий эксперимент. Вычислим локальные векторы PageRank l→J для каждого хоста в STANFORD/BERKELEY. Мы также вычислим глобальный вектор PageRank x→ для STANFORD/BERKELEY, используя стандартный алгоритм PageRank, вектор персонализации u→ которого является равномерным распределением для корневых узлов. Затем мы сравниваем данные локального PageRank для страниц данного хоста и глобального PageRank для страниц в том же хосте. Точнее говоря, мы берем элементы, соответствующие страницам в хосте J глобального вектора PageRank x→, и формируем вектор g→J из этих элементов. Мы нормализуем g→J так, чтобы сумма его элементов равнялась 1 для того, чтобы сравнить его с локальным вектором PageRank l→J, который также имеет L1 норму 1. А именно, g→J = x→(j ∈ J) / ||x→(j ∈ J)||1. Мы именуем этот вектор нормализированными глобальными сегментами PageRank или просто глобальными сегментами PageRank. Результаты представлены в Таблице 3. Абсолютная погрешность ||l→J — g→J||1 составляет в среднем 0,2383 для хостов STANFORD/BERKELEY.
| Аппроксимация | Мера погрешности | Среднее значение |
| l→J | ||l→J — g→J||1 | 0,2383 |
| l→J | KDist(l→J,g→J) | 0,0571 |
| u→J | ||u→J — g→J||1 | 1,2804 |
| u→J | KDist(u→J,g→J) | 0,8369 |
Таблица 3 «Точность», измеренная средней абсолютной погрешностью (а), и (б) KDist расстоянием локальных векторов PageRank l→J и глобальных сегментов PageRank g→J, по сравнению с точностью между равномерными векторами u→J и глобальными сегментами PageRank g→J для массива данных STANFORD/BERKELEY.
Мы сравниваем погрешность локальных векторов PageRank l→j с погрешностью пропорционального вектора u→J = [1/nJ]nx1 для каждого хоста J. Погрешность ||u→J − g→J||1 составляет в среднем 1,2804 для хостов STANFORD/BERKELEY. Очевидно, что вектора локальных PageRank гораздо ближе к глобальным сегментам PageRank, чем пропорциональные векторы. Таким образом, конкатенация локальных векторов PageRank может создать лучший начальный вектор для стандартной итерации PageRank, нежели пропорциональных векторов. Относительная упорядоченность страниц в пределах хоста, вызванная значениями локального PageRank, как правило, близка к внутрихостовой упорядоченности, вызванной значениями глобального PageRank. Для сравнения упорядоченности, мы измеряем среднее «расстояние» между локальными векторами l→J и глобальными сегментами PageRank g→J. Измерение KDist расстояния, основано на τ-коэффициенте ранговой корреляции Кендалла, используется для сравнения приведенной упорядоченности и определяется следующим образом:
Рассмотрим два частично упорядоченных списка URL, τ1 и τ2, длина каждого равняется m. Пусть U — объединение URL-адресов в τ1 и τ2. Если δ1 является U — τ1, то пусть τ’1 будет продолжением τ1, где τ’1 содержит δ1, которое появляется после всех URL-адресов в τ1. 3 Мы продолжаем τ2 аналогично с продолжением τ’2. KDist затем определяется таким образом:
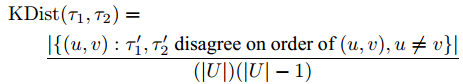
Иными словами, KDist (τ1, τ2) — это вероятность того, что τ’1 и τ’2 расходятся в относительной упорядоченности случайно выбранных пар различных узлов (u,v) ∈ U х U. В данной работе мы только сравниваем списки, содержащие одинаковые наборы элементов, так что KDist идентичен τ-коэффициенту расстояния Кендалла. Среднее расстояние KDist(l→J,g→J) составляет 0,0571 для хостов в STANFORD/BERKELEY. Обратите внимание, что это расстояние небольшое. Это означает, что упорядоченность, вызванная локальными PageRank, близка к правильной, и, следовательно, предполагается, что большинство L1 погрешностей в сравнение локальных и глобальных PageRank происходит от раскалибровки нескольких страниц на каждом хосте. Действительно раскалибровка может произойти с одной из важных страниц, как мы рассмотрим далее, это раскалибровка корректируется на последнем шаге нашего алгоритма. Кроме того, относительный рейтинг страниц на разных хостах неизвестен в этой точке. По этим причинам, мы не рекомендуем использовать локальные PageRank для ранжирования страниц, мы используем их только как более эффективный инструмент для вычисления глобального PageRank.
Таблица 4 подтверждает это наблюдение для хоста aa.stanford.edu. Обратите внимание, что упорядоченность сохраняется, и большая часть несоответствий обусловлена aa.stanford.edu. Вычисление локального PageRank дает слишком мало веса корневому узлу. Так как элементы локальных векторов равняются 1, ранги всех других страницах имеют повышенный вес.
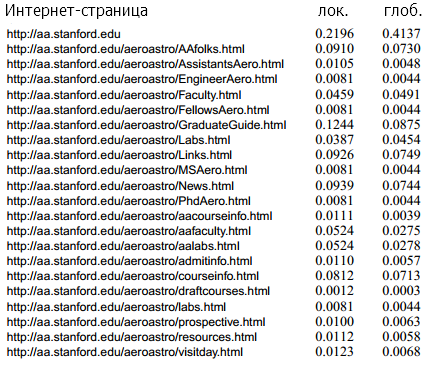
Таблица 4. Вектор локального PageRank для домена aa.stanford.edu (слева) по сравнению с глобальным сегментом PageRank, который соответствует тем же страницам. Вектор локального PageRank имеет аналогичный порядок согласно с нормированными компонентами глобального вектора PageRank. Расхождение фактических рангов во многом это связано с тем, что вектор локального PageRank не имеет достаточного веса корневого узла aa.stanford.edu.
Следует отметить, что погрешности этой модели (где большинство погрешностей L1 происходят из-за раскалибровки нескольких страниц) исправляются легко, так как эти раскалиброванные страницы устраняются (путем, например, нескольких итераций глобального PageRank), остальные страницы становятся на места. Погрешности, которые являются более случайными, занимают больше времени для устранения. Мы наблюдаем это эмпирически, но не включаем эти эксперименты здесь для общего рассмотрения. Это подразумевает критерий остановки для вычисления локальных PageRank. На каждом этапе вычисления локального PageRank, можно высчитать остаточный τ-коэффициент Кендалла (коэффициент расстояния Кендалла τ между текущей итерацией l→(k)J и предыдущей итерации l→(k−1)J). Если остаточный τ-коэффициент Кендалла равен 0, это означает, что упорядочение является правильным, и вычисление локального PageRank можно остановить.
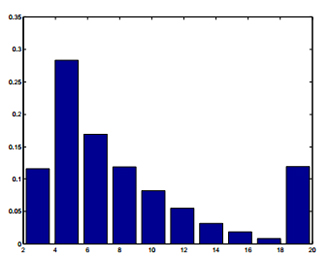
Рис. 4. Скорость сходимости локального PageRank для хостов в DNR-LARGEWEB. Ось х представляет число итераций до сходимости с допустимым значением 10-1, и y-ось — часть хостов, которые сходятся в заданном числе итераций.
4.3.2. Скорость сходимости Local PageRank
Еще один интересный вопрос для исследования, состоит в том, что бы узнать, как быстро сходятся значения локального PageRank. На рисунке 4 показана, гистограмма числа итераций, необходимых для оценки локального PageRank каждого хоста в DNR-LARGEWEB, что бы невязка сходимости в L1 составляла < 10-1. Обратите внимание, что эта невязка сходимости для большинства хостов достигается менее чем за 12 итераций. Интересно, что нет никакой корреляции между скоростью сходимости и размером хоста. Скорость сходимости в первую очередь зависит от распространения вложенных компонентов двусвязаности хоста. То есть, хосты с множеством вложенных компонентов, скорее всего, сходятся медленно, так как они представляют собой медленно развивающиеся цепи Маркова. Хосты с более случайной схемой соединения сходятся быстрее, так как они представляют собой быстро развивающиеся цепи Маркова. Это наблюдение показывает, что можно было бы сделать вычисления локального PageRank даже быстрее, тщательней выбирая компоненты. То есть, если хост имеет множество вложенных компонентов, используйте директории в хостах в качестве ваших компонентов. Тем не менее, это не важнейший вопрос, потому что мы покажем в разделе 5, что вычисления локального PageRank могут быть выполнены в группированном режиме параллельно с поиском. Таким образом, снижение затрат на вычисления локального PageRank не является проблемой для вычисления PageRank при помощи нашей схемы, так как локальные вычисления можно выполнять конвейерным способом вместе с краулингом. 4
В этом разделе мы опишем вычисление относительной важности, или BlockRank, каждого компонента. Предположим, имеются k компонент веба. Что бы вычислить BlockRank’и, для сначала, мы создаем компонент графа В, в котором каждая вершина графа соответствует компоненту веб-графа. Ребро между двумя страницами в вебе можно представить как ребро между соответствующими компонентами (или петлю, если обе страницы находятся в одном компоненте). Взвешенность ребра между компонентами I и J определяется как сумма взвешенности ребер от страницы I к страницам J в веб-графе, взвешенные локальным PageRankом для соединенных страниц в компоненте I. То есть, если A — это веб-граф, а li — локальный PageRank страницы i в компоненте I, то вес ребра BIJ определяется по формуле:
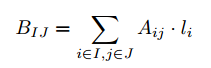
Мы можем записать это в матричной форме следующим образом. Матрица L локального PageRank определяется как n х k матрица, столбцы которой являются векторами локального PageRank l→J.
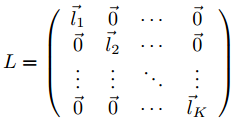
Матрица S — это n х k матрица, которая имеет ту же структуру, как L, но все ненулевые элементы которой заменены на 1. Тогда блочная матрица B является n х k матрицей: B = LTAS. Обратите внимание, что B является матрицей перехода, где элемент BIJ представляет собой вероятность перехода от компонента I к компоненту J. То есть: BIJ = p(J|I). После того как мы получили k х k матрицу перехода B, мы можем использовать стандартный алгоритм PageRank на этой приведенной матрице для вычисления вектора BlockRank b→. То есть:b→ = pageRank(B, u→k, u→k), где u→k постоянный k-вектор [1/k]kx1. Отметим, что вычисление такое же, как для стационарного распределения матрицы перехода c·B+(1−c)Ek, где мы определяем Ek по формуле: Ek = [1]kх1 х u→kT. Аналогия модели случайного пользователя [14] следующая: мы представляем себе, что случайный пользователь переходе от компонента к компоненту в соответствии с вероятностной матрицей перехода B. На каждом этапе, пользователю станет скучно с вероятностью 1 — с и он перейдет к другому компоненту.
В этом разделе мы обнаружим значение глобального вектора PageRank x→. На данный момент, у нас есть два варианта рейтингов. В каждом компоненте J, у нас находится вектор локального PageRank l→J для страниц компонента. У нас также есть вектор BlockRank b→, элементами bJ которого являются BlockRank’и для каждого компонента J, и который определяется измерением относительной важности компонентов. Мы можем теперь провести аппроксимацию глобального PageRank страницы j ∈ J как локального PageRank lj, взвешенного BlockRankа bj компонента, в котором она находится. То есть, x(0)j = lj bJ. В матричной форме это записывается как: x→(0) = Lb→. Напомним, что локальные PageRank каждого компонента равняются 1. Кроме того, BlockRankи равняются 1. Таким образом, наши аппроксимированные глобальные PageRankи также будут равняться 1. Отсюда истекает, что сумма наших аппроксимированных глобальных сумма PageRankов sum(xj) = Σjxj можно записать в виде суммы по компонентам sum(xj) = Σj Σj∈Jxj. Наше определение для xj используем из Уравнения 4.5 sum(xj) = Σj Σj∈Jljbj = ΣJbJ Σj∈JlJ. Так как локальные PageRank и каждого домена равняются 1 (Σj∈Jlj = 1), то sum(xj) = ΣjbJ; и так как BlockRank также равняется 1 (ΣJbj = 1), то sum(xj) = 1. Таким образом, мы можем использовать наш аппроксимированный вектор глобального PageRank x→(0) в качестве начального вектора для стандартного алгоритма PageRank.
Для того чтобы вычислить истинный вектор глобального PageRank x→ из наших аппроксимированных векторов PageRank x→(0), мы просто используем его в качестве начального вектора для стандартных PageRank. То есть: x→ = pageRank(G, x→(0), u→), где G — веб-граф, а u→ равномерное распределение корневых узлов. В разделе 7 мы покажем, как быстро вычислить различные персонализации, если вычислен . BlockRank алгоритм для вычисления PageRank, который представленный в предыдущих разделах, входит в Алгоритм 3, который приведен в Приложении.
Алгоритм BlockRank имеет четыре основных преимущества по сравнению со стандартным алгоритмом PageRank.
Преимущество 1. В основном ускорение нашего алгоритма возникает из-за кэширования. Все компоненты хоста в наших поисках достаточно малы, так что каждый компонент графа помещается в основную память, а вектор рангов для активного компонента в значительной степени вписывается в кэш процессора. Так как полный график не помещается в основной памяти, то итерации локального PageRank требуют меньше дискового ввода/вывода, чем расчеты глобального PageRank. Полные векторы рангов же помещаются в основной памяти, однако, используя отсортированную структуру ссылок 5, значительно улучшают схему доступа к памяти для вектора рангов. В самом деле, если мы будем использовать отсортированную структуру ссылок, предназначенную для BlockRank, в качестве начального вместо стандартного алгоритма PageRank, расширенная локальность ссылок для вектора рангов сокращает время, необходимое для каждой итерации стандартного алгоритма, более чем в 1/2: с 6,5 минут до 3,1 минуты для каждой итерации DNR-LARGEWEB!
Преимущество 2. В нашем алгоритме BlockRank, вектора локального PageRank для многих компонентов будут сходиться быстрее, поэтому вычисления этих блоков могут быть завершены всего после нескольких итераций. Это повышает эффективность вычисления локального PageRank, позволяя тратить больше время вычисления на медленно сходящиеся компоненты, и ускорить расчет быстрый сходящихся компонентов. Обратите внимание, например, на рисунке 4, что существует широкий диапазон скоростей сходимости для компонентов. В стандартном алгоритме PageRank, итерации действуют на весь граф, поэтому сходимость усложняется в значительной степени из-за самых медленных компонентов. Много вычислений тратится на пересчет компонентов PageRank, локальные вычисления которых уже сходились.
Преимущество 3. Вычисление локального PageRank на 1 этапе алгоритма BlockRank может быть проведено в параллельном и распределенном режиме. То есть, локальные PageRankи для каждого компонента могут быть вычислены на отдельном процессоре, или компьютере. Необходимо только, что бы в конце 1-го этапа, каждый компьютер посылал свои вектора локального PageRank l→j на центральный компьютер, который будет вычислять вектор глобального PageRank. Если наш граф состоит из общего количества страниц n, то стоимость обмена связи сети состоит из 8n байтов (при использовании 8-байтовой удвоенной значения с плавающей запятой). Упрощенная параллелизация вычислений, которая не использует компоненты двусвязаности, требует передачи 8n байтов после каждой итерации, что является значительным недостатком. Кроме того, вычисления локального PageRank можно проводить конвейерным способом с веб-поиском. Это означает, что вычисление локального PageRank для хоста может начаться как отдельный процесс, как только заканчивается поиск хоста. В этом случае только недостатки на 2-4 этапах алгоритма BlockRank влияют на ограничение скорости.
Преимущество 4. В нескольких ситуациях, вычисления PageRank (например, результаты 1 этапа) могут быть повторно использованы в течение последующего применения алгоритма BlockRank. Рассмотрим, например, новостные сайты, такие как cnn.com, которые посещают чаще остальных. В этом случае, если мы хотим пересчитать вектор глобального PageRank после поиска cnn.com, мы можем повторить алгоритм BlockRank, кроме того, что на 1 этапе нашего алгоритма, необходимо пересчитать только локальные PageRank для компонента cnn.com. Остальные локальные PageRank не изменятся, и смогут быть использованы на 2-3 этапах. Таким образом, мы можем повторно использовать вычисления локального PageRank для вычисления нескольких «персонализированных» векторов PageRank. Мы обсудим персонализированные PageRank в разделе 7, и обновления графа в разделе 8.
| Шаг | Физическое время |
| 1 | 17 мин. 11 сек. |
| 2 | 7 мин. 40 сек. |
| 3 | 0 мин. 4 сек. |
| 4 | 56 мин. 24 сек. |
| Итого | 81 мин. 19 сек. |
Таблица 5. Время прохождения задания для отдельных этапов BlockRank с с=0,85 для достижения окончательной невязки в масштабах <10-3.
В этом разделе мы исследуем ускорение BlockRank по сравнению со стандартным алгоритмом вычисления PageRank. Ускорение нашего алгоритма для типичных ситуаций происходит из-за первых трех преимуществ, перечисленных в разделе 5.Ускорения связаны с более простыми итерациями, также как с меньшим общим количеством итераций. (Преимущество 4 обсуждается в последующих разделах). Начнем со случая, в котором PageRank рассчитывается после завершения поиска, мы считаем, что только 0 этап алгоритма BlockRank вычисляется одновременно со поискм. Как уже упоминалось в Преимуществе 1 предыдущего раздела, простое улучшение локальности ссылок из-за блочности, под действием лексикографической сортировки матрицы ссылок, обеспечивает ускорение времени в 2 раза, необходимого для каждой итерации стандартного алгоритма PageRank. Это ускорение совершенно не зависит от значения, выбранного для с, и не влияет на скорость сходимости, измеряемую в количествах итераций, необходимых для достижения конкретной невязки L1.
Если вместо стандартного алгоритма PageRank, мы используем алгоритм BlockRank для матрицы компонентов двусвязаности, мы получить максимальную выгоду от 1 и 2 преимуществ, каждый компонент помещается в основной памяти, и многие компоненты сходятся быстрее. Мы сравнивали физическое время, необходимое для вычисления PageRank с использованием алгоритма BlockRank в данном случае, где вектора локального PageRank рассчитывается повторно после завершения поиска. Физическое время, необходимое для вычисления PageRank с использованием стандартного алгоритма приведено в литературе [14]. В таблице 5 приведено время счета для 4 этапов алгоритма BlockRank на массиве данных LARGEWEB. Первые 3 строки в таблице 6 демонстрируют физическое время счета для стандартного PageRank, стандартный PageRank с использованием ссылок, отсортированных по url, и полный алгоритм BlockRank, вычисленный после поиска. Мы наблюдаем небольшое дополнительное ускорение для BlockRank в добавление к описанному ранее ускорению. Затем мы опишем случай, в котором недостатки на 1-3 этапах становятся несущественными, что обеспечивает дальнейшее эффективное ускорение.
| Алгоритм | Физическое время |
| Стандартный | 180 мин 36 сек. |
| Стандартный (используя ссылки отсортированные по url) | 87 мин 44 сек. |
| BlockRank (без конвейеризации) | 81 мин 19 сек. |
| BlockRank (с конвейеризацией) | 57 мин 06 сек. |
Таблица 6 Физическое время для 4 алгоритмов для вычисления PR c = 0.85 с невязкой меньше 10−3.
В следующем случае мы предполагаем, что недостатки на 1 этапе можно сделать незначительными одним из двух способов: вектора локальных PageRank можно вычислять с конвейеризацией вместе с веб-краулингом, или они могут быть вычислены параллельно после сканирования. Что вектора локальных PageRank рассчитывать как можно скорее (например, как только хост будет полностью отсканирован), большинство векторов локальных PageRank будут рассчитаны на момент завершения краулинга. Аналогичным образом, если вектора локальных PageRank рассчитывать после сканирования, но рассредоточенным образом, используя несколько процессоров (или машин) для вычисления векторов PageRank самостоятельно, время, необходимое для вычисления локального PageRank будет ниже по сравнению со стандартным вычислением PageRank. Таким образом, только время вычисления 2-4 этапов для BlockRank будут значимыми при расчете ускорения. Структура B является значительным недостатком 2 этапа, но это тоже можно вычислить конвейерным способом; 3 этап имеет незначительные недостатки. Таким образом, ускорение BlockRank в этом случае определяется увеличением скорости сходимости на 4 этапе, что возникает в результате использования аппроксимации BlockRank x→(0) как начального вектора. Теперь тщательно рассмотрим относительную скорость сходимости. На рисунке 5 (а), показана скорость сходимости стандартных PageRank, по сравнению со сходимости 4 этапа BlockRank для массива данных STANFORD/BERKELEY при вероятности случайного прыжка 1-с = 0,15 (т. е. с = 0,85). Обратите внимание, что достижение значения невязки сходимости 10-4, используя начальный вектор BlockRank, приводит к ускорению вычисления массива данных STANFORD/BERKELEY в 2 раза. Набор данных Массив данных LARGEWEB привел к увеличению скорости сходимости в 1,55 раза. Эти результаты приведены в таблице 7. В сочетании с первым эффектом (сортирования структуры ссылок), описанным выше, наш алгоритм обеспечивает ускорение более чем в 3 раза. (Для более высоких значений с, исследованных в литературе [11], ускорение является еще более значительным, например, мы получили 10-кратное ускорение на массиве данных STANFORD/BERKELEY, когда с = 0,99).
| Google PageRank | BlockRank | |
| STANFORD/BERKELEY | 50 | 27 |
| LARGEWEB | 28 | 18 |
Таблица 7 Количество итераций, необходимых для сходимости стандартного PageRank и BlockRank (с допустимым значением 10−4 для STANFORD/BERKELEY и 10−3 для LARGEWEB).
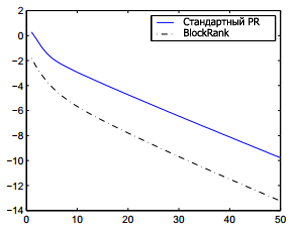
Рис. 5. Скорость сходимости для стандартного PageRank (сплошная линия) по сравнению с BlockRank (пунктирная линия). Ось х — число итераций, а y-ось – логарифм невязки L1. Массив данных STANFORD/BERKELEY; с = 0,85.
Эти результаты ускорения для вычисления PageRank являются наибольшими на сегодняшний день, значительное ускорение наблюдается только при с = 0,85 для больших массивов данных. Кроме того, следует отметить, что алгоритм BlockRank можно использовать в сочетании с другими методами ускорения PageRank, такими как квадратичная экстраполяция [11], или Гаусса-Зейделя [6, 1] (или оба). Эти методы просто применить к 4 этапу алгоритма BlockRank. Если использовать сочетание этих методов, то следует ожидать еще более быстрой сходимости для BlockRank; эти смешанные методы будут исследоваться далее.
В литературе [14], первоначально предположили, что, изменяя вектор случайного перехода, чтобы он был непостоянным, главный вектор PageRank может быть смещен к определенным видам страниц. Например, случайный пользователь, интересующийся спортом, может переходить время от времени на www.espn.com, а случайный пользователь, интересующийся текущими событиями, может вместо этого перейти на www.cnn.com. В то время как персонализированный PageRank является захватывающей идеей, которая, кстати говоря, может оказать существенное влияние на продвижение сайтов в органической выдаче, в общем-то, требует вычисления большого числа векторов PageRank.
Мы используем алгоритм BlockRank и ограничения на поведение перехода случайного пользователя, что значительно сократит время расчета персонализированного PageRank. Ограничение заключается в следующем: вместо того, чтобы иметь возможность выбирать распределение страниц, на которые переходит случайный пользователь, можно выбрать хосты. Например, случайный пользователь, интересующийся спортом, может перейти к хосту www.espn.com, но он не может, например, перейти к www.espn.com/ncb/columns/forde pat/index.html. Мы можем кодировать персонализированный вектор в k-мерном векторе u→k (где k — число компонентов хоста в вебе), который является распределением по различным хостам.
С этим ограничением векторы локального PageRank l→J не будут изменяться для различных персонализаций. Получается, что, так как вектора локального PageRank l→J не меняются для различных персонализаций, не меняется и блочная матрица B. Для различных персонализаций будет меняться только вектор BlockRank b→. Таким образом, нам нужно только пересчитать вектор BlockRank b→ для каждого блока персонализации вектор u→k. Вычисления персонализированного PageRank можно провести следующим образом. Если предположить, что вы уже вычислили общий вектор PageRank один раз, используя алгоритм BlockRank, и запомнили блочную матрицу перехода B, то алгоритм персонализированного BlockRank — это просто последние 3 этапа общего алгоритма BlockRank.
Алгоритм персонализированного BlockRank требует, чтобы случайный пользователь не имел возможности перехода к определенной странице (он может только переходить к хосту). Тем не менее, последний этап в алгоритме BlockRank требует вероятностного распределения случайного перехода u→ к страницам. Таким образом, нам нужно вызвать вероятность p(j) случайного перехода пользователя на страницу j, если мы знаем, что с вероятностью p(J) он перейдет на хост J, в котором находится страница J. Мы вызываем эту вероятность следующим образом:
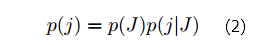
То есть, вероятность того, что случайные переходы пользователя на страницу j –это вероятность того, что он перейдет на хост J, кратна вероятности перехода на страницу J учитывая, что он находится в хосте J. Поскольку вектор локального PageRank l→J является стационарным распределением вероятности страниц в хосте J, p(j|J) задается элементом l→J, который соответствует странице j. Таким образом, элементы LjJ матрицы L соответствуют LjJ = p(j|J). Кроме того, по определению, элементы (vk)J = p(J). Таким образом, Уравнение 2 в матричной форме записывается как u→ = Lu→k.
Если мы уже вычислили общий вектор PageRank x→, у нас есть еще «лучшие» локальные вектора PageRank, с которых нужно начать. То есть, мы можем нормализовать сегменты x→ для формирования нормированных глобальных сегментов PageRank g→J, как описано в разделе 4. Эти показатели, конечно, лучше оценивают относительные величины страниц в компоненте, чем вектора локального PageRank l→J, так как они являются производными от общего вектора PageRank для всего веба. Таким образом, мы можем изменить персонализированный BlockRank следующим образом. Давайте определим матрицу H аналогично тому, как мы определили L, исключая использование нормированных глобальных сегментов PageRank g→J, а не векторов локального PageRank l→J. Опять же, нам нужно вычислить H всего один раз. Определим матрицу BH, как определяли матрицу B в уравнении 4.4, но с использованием H вместо L:
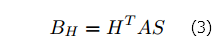
Проверим этот алгоритм, вычисляя персонализированный PageRank случайного пользователя, который является аспирантом в области лингвистики в Стэнфорде. Существует 80% вероятности того, что он перейдет на лингвистический хост www-linguistics. stanford.edu, и 20% вероятности перехода к основному хосту Стэнфорда www.stanford.edu. Рисунок 6 показывает, что ускорение вычисления персонализированного PageRank для этого пользователя имеет сопоставимые преимущества перед ускорением стандартного BlockRank. Тем не менее, основным преимуществом является то, что вектора локального PageRank вообще не нужно вычислять для персонализированного BlockRank. Матрица H формируется из уже вычисленного общего вектора PageRank. Таким образом, дополнительные сложности для расчета векторов персонализированного PageRank с помощью алгоритма персонализированного BlockRank минимальны.
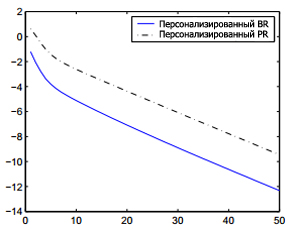
Рисунок 6. Сходимость вычисления персонализированного PageRank с использованием стандартного PageRank и персонализированного BlockRank.
Мы также можем использовать стратегию повторного использования векторов локального PageRank, когда мы хотим пересчитать PageRank после добавления или удаления нескольких страниц в Интернете. Так как Интернет является очень динамичным и веб-страницы добавляются и удаляются постоянно, это является важной проблемой для решения. В частности, мы хотели бы найти определенные хосты, такие как агентства ежедневных новостей, как cnn.com, чаще, чем другие.
Если мы используем BlockRank для вычисления вектора PageRank x→, и сохраняем вектора локального PageRank l→J, то нам всего лишь нужно пересчитать локальные PageRank тех хостов, к которым были добавлены или удалены страницы при каждом обновлении.
Мы показали, что гиперссылки веб-графа имеют вложенные компоненты двусвязаности, то, что еще не было тщательно исследовано в работах, касающихся веб-сети. Мы используем эту двусвязаность для быстрого вычисления PageRank, используя алгоритм, который мы называем BlockRank. Мы показывали эмпирически, что BlockRank ускоряет вычисления PageRank в 2 раза и выше, в зависимости от конкретной ситуации. Существует целый ряд задач для будущей работы: найти «лучший» компонент для BlockRank путем разложения медленно взаимодействующих компонентов с внутренними вложенными компонентами двусвязаности; использование компонентов двусвязаности для алгоритмов, основанных на гиперссылках, кроме как веб-поиска, таких как группирование или классификация; а также более тщательное изучение тем об обновлениях и персонализации PageRank.
Эта статья основана на работе при частичной поддержке «Национального Научного Фонда» по гранту № IIS-0085896 и Грант № CCR-9971010, и научно-исследовательского сотрудничества между лабораториями теории связи Nippon Telegraph and Telephone Corporation и CSLI, Стэнфордского университета (исследовательский проект по концептуальным базам лингвистического усвоения и логического понимания).
Перевод материала «Exploiting the Block Structure of the Web for Computing PageRank» выполнил Сергей Неиленко
Полезная информация по продвижению сайтов:
Перейти ко всей информации