SEO-Константа
Яндекс.Директ + оптимизация
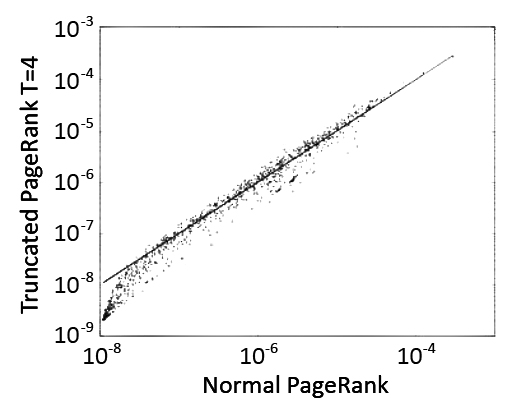
В прошлой части нашего с вами материала мы представили вам сам алгоритм Truncated PageRank, при сравнении же полученных значений Truncated PR с Google PageRank для графа доменов расположенных в зоне .UK мы наблюдаем очень сильную корреляцию между данными показателями, однако она становится более слабой по мере усечения уровней. Мы не будем спорить на предмет того, стоит ли использовать Truncated PageRank в качестве замены классическому алгоритму Google, но исходя из тех результатов, которые мы получим ниже, можно открыто утверждать то, что исследование отношений между этими двумя алгоритмами предоставляет нам очень много полезнейшей информации, которую следует использовать в целях обнаружения ссылочного спама. Сравнение классического алгоритма и его модификации (значения T составляли от 1 до 4) представлено на Рис.21
В данном разделе мы опишем методологию вычисления числа саппортеров для всякой вершины нашего графа, но так как определить их количество на большом интернет-графе представляется для нас невозможным, то в своей работе мы будем использовать рандомизированный алгоритм вероятностного подсчета (разработан Р. Моррисом в 1978 году), более точный для малых расстояний, нежели чем тот его эквивалент, который представлен в [1]. Предложенный нами метод является достаточно простым в своей реализации и распараллеливании, в то же самое время его можно рассматривать как обобщение алгоритма ANF (Approximate Neighborhood Function) [2].
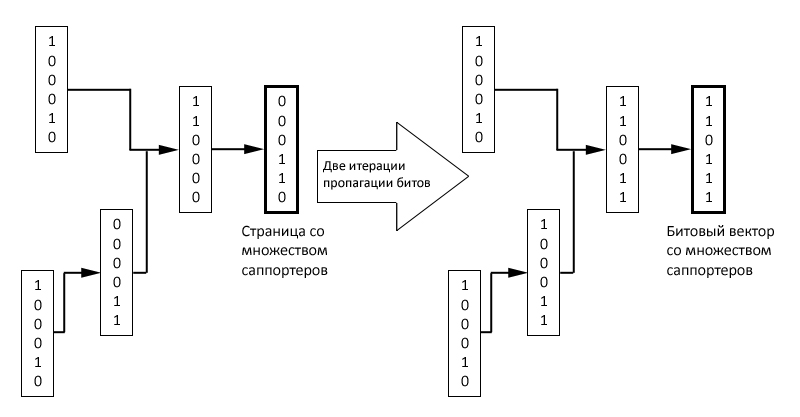
Рис. 22 Схематическое представление алгоритма пропагации битов с двумя итерациями
Мы начнем с того, что присвоим каждой интернет-странице случайный битовый вектор. Затем, в случае обнаружения на какой-либо странице y гиперссылки на страницу x, мы будем обновлять битовый вектор документа х до x ↔ x OR y. По истечению некоторого числа итераций (две из них представлены на Рис. 22), битовый вектор ассоциированный со страницей x предоставит нам информацию по количеству её саппортеров на некотором расстоянии.

Рис. 23. Алгоритм пропагации битов для одновременного вычисления различных саппортеров в интернет-графе на расстоянии ≤ d.
Укажем, что вычисление числа саппортеров для всех вершин веб-графа может выполняться одновременно как с подсчетом Truncated PageRank, так и классического Google PR; основной алгоритм требует O(kN) бит памяти; может работать в потоковой модели ссылочного графа, заданного списком смежности (то есть для каждой вершины будет обозначен перечень всех смежных с нею вершин) и прочитанного d-раз. Две его адаптации, которые будут представлены несколько позже, потребуют схожий объем памяти и считывают интернет-граф O(d logN) или в среднем O(d logNmax(d)) раз, где Nmax(d) означает максимальное количество интересующих нас саппортеров в пределах расстояния d.
Нотация. Пусть Vi будет битовым вектором, ассоциированный с какой-нибудь страницей, i=1,…..,N. Тогда, за x обозначим конкретный веб-документ, а за S(x,d) — множество его саппортеров на некотором определенном расстоянии d. Пускай N(x,d)= |S(x,d)|. Давайте вернемся к Рис. 18 из предыдущей части нашего с вами материала, где были изображено распределение саппортеров на двух больших интернет- графах, и исследуем типичные значения, принимаемые d на интервале 1 ≤ d ≤ 20. В дальнейшем для простоты мы будем писать S(x) и N(x) для S(x,d) и N(x,d), рассматривая какое-либо конкретное значение d.
INIT (узел,бит): на шаге инициализации j-ый бит Vi устанавливается в 1 с вероятностью ε, независимо для всех i =1,….,N и j = 1,…..,k (ε является параметром алгоритма, подбор которого объясняется несколько ниже). Поскольку ε фиксирована, мы можем уменьшить количество обращений к генератору случайных чисел, генерируя их в соответствии с геометрическим законом распределения с параметром 1 — ε, а затем пропуская соответствующее количество позиций перед установкой бита. Это особенно полезно в том случае, когда параметр ε является малым.
ESTIMATE (V[узел,⋅]): рассмотрим страницу x, и обозначим ее битовый вектор за Vx, а i-ый компонент за xi, i = 1,….,k. В силу свойств оператора OR и независимости xi имеем:
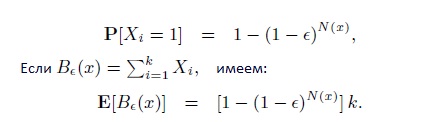
В том случае, если б нам было бы известно E[Be(x)], мы могли бы подсчитать N(x) достаточно точно, однако на практике для всякой страницы x мы можем дать всего лишь предположительную оценку B—e(x) количества ее саппортеров. Получаем:
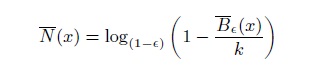
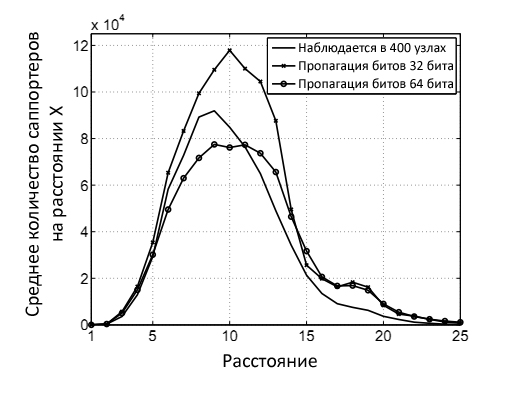
На Рис. 24 показан результат работы основной версии алгоритма с ε = 1/N на 860,000 узлах веб-графа в доменной зоне EU.INT с использованием 32 и 64 бит. Несмотря на то, что при текущих значениях k, мы можем провести оценку среднего числа саппортеров, для достижения конечных целей настоящего исследования данный факт не является достаточным, так как нас интересуют далеко не все узлы, а только те, которые отличаются своей спецификой. По этой причине нам потребуется несколько модифицировать наш базовый алгоритм.
Для того, чтобы получить необходимую для нас информацию давайте предположим, что нам известно N(x) и ε = 1/N(x), тогда имеем:
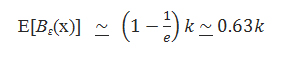
Получаем более хорошую аппроксимацию для всех интересующих нас значений N(x,d). Кроме того, так как E[Be(x)] является монотонной функцией в ε, равно возрастанию ε с малых значений до превышающих 1/N(x), мы также можем ожидать и увеличение значений B—e(x) с малого до большего, нежели чем (1 — 1/e)k. Грубо говоря, основная идея адаптивной версии алгоритма (см. Рис. 25) заключается в том, чтобы, начиная со значения εmin (к примеру, εmin = 1/N), удваивать сей параметр на каждой итерации до достижения некоторого Emax (к примеру, εmax = 0.5). В какой-то момент ε примет такое значение ε(x), при котором ε(x) ≤ 1/N(x) ≤ 2ε(x). В идеале при увеличении параметра ε со значения ε(x) до 2ε(x), Be(x) должно сдвинуться со значения меньшего чем (1 — 1/e)k ко значению большему, нежели чем (1 -1/e)k. Здесь, безусловно, не существует прямой детерминированности, однако это произойдет с достаточно высокой долей вероятности в том случае, если k достаточно велико.

Рис. 25. Адаптивная версия алгоритма пропагации битов для приблизительно подсчета количества различных саппортеров во всех узлах графа. Адаптация вызывает нормальный алгоритм пропагации с различными значениями ε некоторое число раз.
Лемма. Итерация адаптивной версии алгоритма пропагации выполняется не более log2(εmax/εmin)= O(log2N) раз. Обратите внимание на то, что при малых значениях k мы можем иметь ложные срабатывания алгоритма, то есть таких ситуаций, при которых в некоторой вершине x получаем Bе(x) > (1 — 1/e)k для ε < ε(x) или Bе(x) < (1 — 1/e) k для ε > ε(x). Однако, как уже было подмечено выше, подобного не случится при больших значениях k, а доказательством тому являются стандартные границы Чернова [3].
Теорема. Всякий раз, когда 0.018 k ≥ 1, для каждого x:
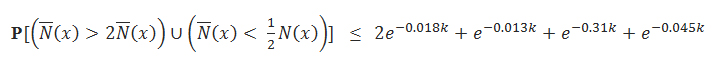
,где N—(x) означает приблизительную оценку N(x). Также делается допущение, что ε—=1/N—(x). В данном материале мы не станем доказывать теорему, но подчеркнем, что анализ нашего метода представляется куда более простым, нежели чем тот, что представлен в [1]. Причина заключается в том, что вероятностный анализ в [1] требует подсчета средней позиции младшего по значимости бита, который не устанавливается в соответствующей генерации потока случайных битов. Более того его вычисление не может быть выполнено прямым способом. В нашем же случае, по причине того, что каждый Bе(x) представляет собой сумму двоичных независимых случайных величин, мы можем легко определить как математическое ожидание, так и точные границы вероятности его отклонения от установленного коэффициента.
Для быстроты все свои эксперименты мы начинали не с минимального значения, а с εmax = 1/2, разделяя впоследствии ε надвое на каждой итерации, а не умножая как это описывалось ранее. Почему? В нашем случае мы имеем дело с малыми расстояниями, а следовательно, с такой окружающей средой, которая состоит из сотен или тысяч узлов. Мы фиксируем полученные оценки для интересующего нас узла при Bе(x) < 0.63k, и прекращаем итерации алгоритма при 1% или меньшем количестве узлов, имеющих Bе(x) ≥ 0.63. На Рис. 26 показано, что количество итераций адаптивного алгоритма пропагации битов, необходимых для приблизительных оценок окружающей среды на расстоянии 4 (или меньшем), составляет 15, а для всех расстояний находящихся в пределах 8 — менее чем 25.
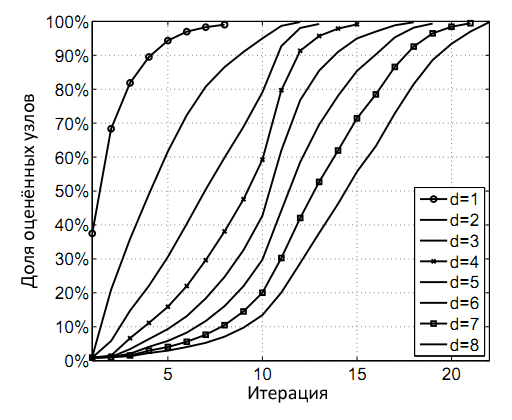
Рис. 26. Доля надлежащим образом оцененных узлов, полученных по истечению некоторого числа итераций. Например, 15 итераций вполне достаточно для получения надлежащих оценок для 99% узлов на расстоянии d=4.
Помимо того адаптивного метода оценки, который был представлен вам выше, сейчас мы опишем вам еще один способ, который заключается в следующем: всякий раз, когда в начале имеем Bе(x) < 0.63k мы вычисляем N—(x) дважды, используя основной алгоритм оценки саппортеров с Bе(x) и B2е(x), а затем усредняем результаты полученных оценок. Мы называем это комбинированной оценкой (вероятность ошибки при ее применении на практике является крайней низкой), использующей как информацию из Е, так и количество битовых наборов. Мы также сравнили точность работы нашего алгоритма с методом ANF [2]. В ANF размер битовой маски напрямую зависит от размера графа, в то время как число производимых итераций (в [2] обозначается за k) обусловливается необходимостью достижения требуемой точности. Наш же подход является ортогональным, и количество итераций будет напрямую зависеть от масштабов интернет-графа, а для достижения необходимой точности будет использоваться битовая маска. Для того, чтобы сравнение двух алгоритмов выглядело достаточно объективно, давайте рассмотрим продукт отношений между размером битовой маски и количеством
итераций как некий параметр, характеризующий использование общего числа битов на узел. Для начала зафиксируем в ANF размер битовой маски в 24, поскольку 224 = 16М является ближайшим значением для 18 млн. узлов в нашей веб-коллекции, а затем запустим алгоритм ANF с 24 (соответствует 24 бит х 24 итераций ) и 48 (соответствует 48 бит х 48 итераций) итерациями. Само сравнение алгоритмов представлено на Рис. 27, и, если вы заметите, то первый показатель немного больше того, который необходим для нашего алгоритма на расстоянии 1, в то время, как последующий — аналогичен его требованию на расстоянии 5 (единственный плюс максимального расстояния в том, что мы используем его для детекции спама).
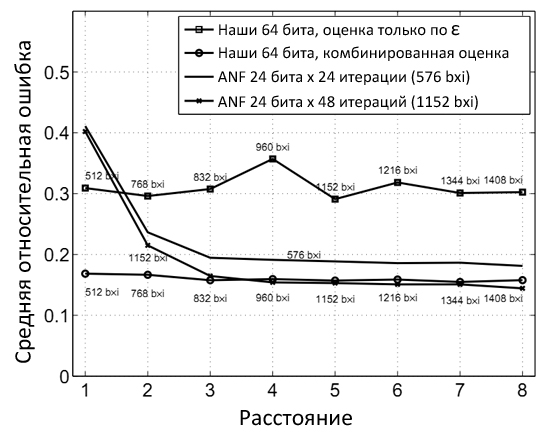
Рис. 27. Средняя относительная ошибка различных стратегий.
Получается, что несмотря на то, что основной алгоритм оценки одинаково хорошо работает на всем диапазоне выбранных расстояний, совместное использование ANF и алгоритма комбинированных оценок, позволяет добиться еще более лучших результатов. В частности, наш комбинированный алгоритм работает лучше, чем ANF на расстоянии до 5 в том смысле, что у него имеется наилучший показатель по средней относительной ошибке и/или здесь он показывает наилучшую производительность при использовании меньшего объема имеющихся бит. Однако для больших расстояний техника вероятностного подсчета , используемая в ANF, оказывается куда более эффективной. Важно также отметить, что на практике, даже если мы выбираем 24-х битовую маску для стандартного вероятностного подсчета, чем мы собственно и занимались в наших экспериментах, для каждого узла выделяется по 32 бита, 8 из которых не используются алгоритмом. В нашем же подходе мы можем использовать их для увеличения точности, что особенно важно при работе с большими объемами данных.
Одним из ключевых вопросов в борьбе с поисковым спамом является проблема предоставления прямых технологий, позволяющих поисковым системам определять степень доверия к той или иной страницы или сайту. Мы создали набор классификаторов тестирующих эффективность метрик, которые описываются нами в части автоматической классификации web-документов.
Наша цифровая коллекция (была скачена в 2002 году) состояла из 18.5 млн. интернет-страниц, расположенных на 98,452 различных хостах в доменной зоне .UK. Учитывая большие масштабы нашей коллекции мы решили заниматься классификации не каждой отдельной страницы, а вести свою работу по хостам. Несмотря на то, что такой подход влечет за собою допущение ряда ошибок, как, например, смешение спам страниц с качественным контентом, он позволяет достичь большего вершинного покрытия за счет сокращения узлов графа. Сама мануальная классификация заняла у нас примерно 3 дня. Так как классификатор требует классовой разметки, мы вручную проверили образцы 5,750 хостов (5.9%), что является покрытием для 31.7% веб-документов нашей коллекции. Мы также сравнили несколько вручную отобранных страниц с каждого хоста с теми списками URL-ов, которые были обнаружены в процессе сканирования хостов краулером. Всякий раз, когда мы обнаруживали ссылочную ферму внутри хоста, мы классифицировали как спам исключительно все его содержимое и, тем не менее, в нашей практической работе мы наблюдали смешение спам страниц и качественного контента на одном хосте очень редко. Как и в [4,5] мы отнеслись с определенной степенью предвзятости к тем хостам, которые имели высокий Google PageRank, однако мы не учитывали в своей классификации такие параметры, как длина хостов и общее количество страниц расположенных в узлах по той простой причине, что это выходит за рамки текущего ссылочного анализа. Еще на этапе ручной проверки мы отказались от 7% хостов по причине их недоступности, а оставшиеся 5,344 были разделены на три класса:
Спам (16%). Хосты явно содержали в себе ссылочные фермы; использовали ключевые слова в хостах («order-website-optimization.wseob.ru»), директориях или файлах; осуществляли автоматическую переадресацию на другой хост.
Норма (81%). Хосты явно не содержат в себе ссылочные фермы, иными словами — это НЕ-спам или «ham»-элементы.
Подозрительные (3%). Пограничные элементы, к числу которых мы отнесли: нелегальный бизнес (сайты казино, фармацевтика без рецепта) и взрослую тематику, так как все они используют для своего продвижения ссылочные фермы; сюда же включены сайты, заимствующие чужой контент или наполняющие свое содержимое рекламой; сети аффилиатов; группы тех хостов, которые были созданы по шаблону с небольшими вкраплениями текстовой информации. Следуя консервативному подходу, при автоматической классификации мы объединили данный класс с нормальными хостами.
| Класс | Хосты | Страницы |
| Спам | 840 (16%) | 329К (6%) |
| Норма | 4,333 (81%) | 5,429К (92%) |
| …Подозрительные | 171 (3%) | 118К (2%) |
| ВСЕГО | 5,344 (5.8%) | 5,877К (31.7%) |
Табл. 3. Количество хостов и страниц в каждом классе.
Несмотря на то, что в нашей коллекции существует множество сайтов, оптимизированных под поисковые системы, они, тем не менее, предлагают своим пользователям полезную информацию. Поэтому мы приняли решение отнести продвижение сайтов в «серую» зону между теми сайтами, которые придерживаются этики поисковых машин, и теми ресурсами, которые следуют неэтичным, спаммерским методам своей раскрутки в сети.
В качестве ссылочных метрик мы использовали ряд характеристик, в том числе Google PageRank, Truncated PageRank с расстояниями d=1,2,3 и 4, а также произвели адаптивную оценку числа саппортеров на аналогичных расстояниях. Так как все они были рассчитаны для конкретных страниц, нам пришлось привязать их к хостам путем вычисления по домашней странице хоста (URL соответствующий корневой директории) и страницы с максимальной высоким значением PageRank — довольно часто складывается ситуация (для страниц нашей выборки отличие составило 62%), при которой наибольшую голосующую способность имеет отнюдь не главная страница хоста. Классифицированные хосты, отнесенные к ранее уже описанным классам «спам» и «норма+подозрительные», составляют учебный набор для процесса обучения нашего алгоритма.
Мы экспериментировали с реализованными Weka [6] классификационными деревьями, построенных с помощью алгоритма Джона Квинлана C4.5. Сам алгоритм дерева решений C4.5 является усовершенствованной версией ID3, отличительной чертой которого стала возможность отсекать ветви, работать с числовыми атрибутами и строить дерево из обучающей выборки, имеющей пробелы в значениях ряда атрибутов. Мы производили оценку обучающих схем с применением 10-fold кросс-валидации, то есть количество блоков равно поделенного исходного множества было равно десяти. В качестве метрики ошибок мы использовали измерения точности и полноты из информационного поиска [7], учитывая задачу детекции спама:

Ложное срабатывание и пропуск являются двумя типами ошибок в классификации спама:

Здесь мы учли такие возможные комбинации предыдущих ссылочных особенностей, как, например: соотношение саппортеров на расстоянии d и саппортеров, находящихся на расстоянии d-1; соотношение Truncated PageRank на расстоянии d и классического Google PR; минимальное соотношение соседей на расстоянии d и на дистанции d-1, и т.д. В общей сложности, мы использовали 82 дифференциальных признака. После завершения этапа по созданию дерева решений, на этапе его редукции, в целях оптимизации производительности мы также выполняем сокращение, уменьшающее ошибки. Для начала мы запустили свой алгоритм с минимальных 5 до 30 хостов в листе(параметр М) дерева, получив дерево решений с 49 и 31 правилом. Заметим, что мы ограничиваем объем узлов в листе во избежании переобучения, а также для того, чтобы иметь меньший набор правил. В Табл. 2 представлена оценка производительности классификации, основанной на комбинации Truncated PageRank и приблизительного подсчета саппортеров.
| Отсечение | Правила | Спам класса | Ошибки | ||
| Точность | Полнота | Ложные срабатывания | Пропуски | ||
| М = 5 | 49 | 0.87 | 0.80 | 2.0% | 20% |
| М = 30 | 31 | 0.88 | 0.76 | 1.8% | 24% |
| Без сокращения | 189 | 0.85 | 0.79 | 2.6% | 21% |
Табл. 4. Оценка комбинированного классификатора. М — минимальное количество хостов на лист.
Кроме этого, мы также сгенерировали дерево решений без шага по сокращению, уменьшающего ошибки (REP), которое уже имело 189 правил. Данное дерево не улучшило производительности по сравнению с тем, которое имело 49 правил и определило 80% поискового спама с показателем ошибок равным 2%.
Мы подготовили алгоритм доверия Google TrustRank [5, 8] для его тестирования на нашей веб-коллекции документов. Алгоритм TrustRank, о котором мы писали в самом начале нашего с вами материала посвященному детекции поискового спама, является хорошо-известным методом для разделения высококачественных авторитетных страниц сайтов / хостов от прочих документов, то есть спама и низкокачественных ресурсов. Он создает такую метрику, которая может быть использована для ранжирования, а в сочетании с классическим Google PageRank использоваться как инструмент для понижения спама в выдаче. Напомним, что расчет TrustRank начинается с некоторого набора страниц, имеющих мануальную пометку как «траст», затем совершается серфинг в определенное количество шагов (обычно около 20) и, наконец, возвращение к исходному «трасту» с некоторой вероятностью на каждом шагу (обычно 0.15). Полученная вероятность достижения страницы является ее оценкой и страница с низким показателем траста вкупе с высоким значением PR будет считаться подозрительной, поскольку лишь при цитируемости сайта с содержимого наиболее релевантных страниц, расположенных во внешней виртуальной среде, наша интернет-страничка будет иметь высокую голосующую способность. Для формирования набора трастовых узлов мы использовали данные Open Directory Project (dmoz.org), в результате чего мы имели 32,866 хостов, имеющих минимум одну страницу в каталоге ODP, а следовательно и высокую степень доверия (в отличие от всего объема в 98,452 хоста) с нашей стороны. На основании алгоритмов Google TrustRank, Truncated PageRank и оценки саппортеров, мы построили три классификатора. Их точность после 10-fold кросс-валидации представлена в Табл. 5 и 6
| Классификаторы (сокращение с М=5) | Спам класса | Ошибки | ||
| Точность | Полнота | Ложные срабатывания | Пропуски | |
| Google TrustRank | 0.82 | 0.50 | 2.1% | 50% |
| Truncated PageRank, t=2 | 0.85 | 0.50 | 1.6% | 50% |
| Truncated PageRank, t=3 | 0.84 | 0.47 | 1.6% | 53% |
| Truncated PageRank, t=4 | 0.79 | 0.45 | 2.2% | 55% |
| Оценка саппортеров, d=2 | 0.78 | 0.60 | 3.2% | 40% |
| Оценка саппортеров, d=3 | 0.83 | 0.64 | 2.4% | 36% |
| Оценка саппортеров, d=4 | 0.86 | 0.64 | 2.0% | 36% |
| Классификаторы (сокращение с М=30) | Спам класса | Ошибки | ||
| Точность | Полнота | Ложные срабатывания | Пропуски | |
| Google TrustRank | 0.80 | 0.49 | 2.3% | 51% |
| Truncated PageRank, t=2 | 0.82 | 0.43 | 1.8% | 57% |
| Truncated PageRank, t=3 | 0.81 | 0.42 | 1.8% | 58% |
| Truncated PageRank, t=4 | 0.77 | 0.43 | 2.4% | 57% |
| Оценка саппортеров, d=2 | 0.76 | 0.52 | 3.1% | 48% |
| Оценка саппортеров, d=3 | 0.83 | 0.57 | 2.1% | 43% |
| Оценка саппортеров, d=4 | 0.80 | 0.57 | 2.6% | 43% |
Наилучшим единичным классификатором является тот, который основан на оценке саппортеров, поскольку он позволяет обнаружить 57%-64% поискового спама с 2,1% — 2% ложных срабатываний. Далее следует классификатор на основе TrustRank, который смог вычислить 49%-50% спама при 2,3%-2,1% ошибок; Truncated PageRank замыкает тройку с 43%-50% определенного им спама и 1,8%-1,6% ложных срабатываний. Однако ни одна из единичных техник не дает столь превосходных результатов, какие получаются в случае применения комбинированного классификатора (см. Рис. 28).
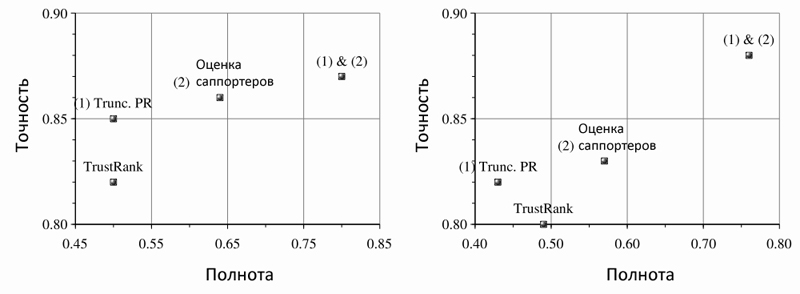
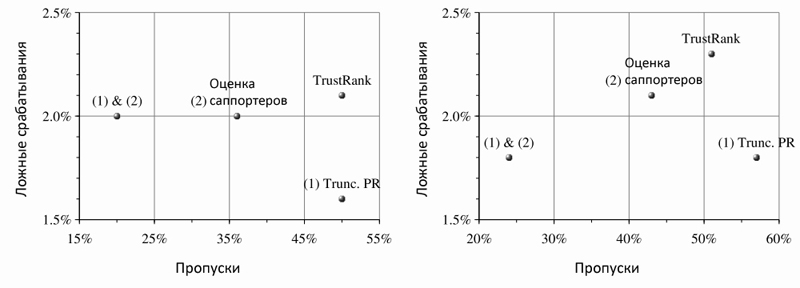
Рис. 28. Сравнение единичных и комбинированного классификатора, использующего все вышеупомянутые алгоритмы. Слева: отсечение с М=5. Справа: отсечение с M = 30.
Страница материала:
Детекция поискового спама. Часть 1: Введение в алгоритм Google TrustRank
Детекция поискового спама. Часть 2: Расчет алгоритма Google TrustRank
Детекция поискового спама. Часть 3: От TrustRank к алгоритмам HostRank и DirRank
Детекция поискового спама. Часть 4: HostRank или PageRank, вычисляемый по графу хостов
Детекция поискового спама. Часть 5: От DirRank к алгоритму Truncated PageRank
Детекция поискового спама. Часть 6: Truncated PageRank и Вероятностный Подсчет
Детекция поискового спама. Часть 7: Знакомство с алгоритмом BadRank, обнуляющим Google PageRank
Детекция поискового спама. Часть 8: Google BadRank и ParentPenalty
Детекция поискового спама. Часть 9. Введение в алгоритм SpamRank
Детекция поискового спама. Часть 10: От исследования SpamRank к алгоритму Anti-TrustRank
Детекция поискового спама. Часть 11: Эксперименты с алгоритмом недоверия Anti-TrustRank
Детекция поискового спама. Часть 12: Применение принципов термодиффузионной
Детекция поискового спама. Часть 13: Детальный анализ алгоритма ранжирования DiffusionRank
Детекция поискового спама. Часть 14: Вычисление AIR на веб-графе, эквивалентного электронной схеме
Детекция поискового спама. Часть 15: Применение искусственных нейронных сетей
Полезная информация по продвижению сайтов:
Перейти ко всей информации