SEO-Константа
Яндекс.Директ + оптимизация
Как уже упоминалось в предыдущей части нашего с вами материала, в ряду случаев наличие висячих узлов может оказывать существенное влияние на ранжирование документов в органическом поиске. Ориентируясь на Рис. 14 можно сказать, что как при равномерном, так и неравномерном перемещении пользователя наша с вами виртуальная страница получает более высокое значение Google PR.
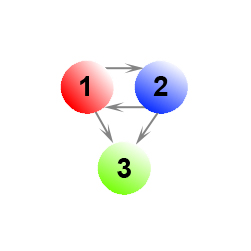
Например, при допущении равномерного перемещения с какого-либо висячего документа к прочим страницам нашей системы мы бы имели следующую матрицу переходов:
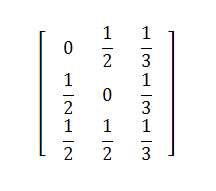
В ином случае мы можем обозначить за С={1, 2} то подмножество узлов нашей модели, которое имеет сильную связанность, а прочие узлы, на которое подмножество С ссылается лишь в одностороннем порядке обозначим за D={3}. Тогда матрица переходов (α= 0.85) принимает вид:

Отсюда, нормированное значение PageRank (x1, x2, z) = (0.31746, 0.31746, 0.365079). Надо сказать, что виртуальная страница может получать существенно большее значение веса Google PR даже при введении запрета на телепортацию в ее содержимое пользователя поисковой системы.
Если само по себе признание документа висячим, еще не ставит под сомнение качество содержащегося в нем контента (мы можем иметь дело с аналитическими отчетами, научными публикациями и т.д.) и поисковая система всегда может произвести все необходимые оценки его содержимого, то ситуация с теми веб-ресурсами, которые возвращают клиентские ошибки вида 404 Not Found (документ не найден и/или не существует) или 403 Forbidden (доступ к ресурсу был запрещен) обстоит совершенно по-иному. Существуют две основные причины появления подобного рода ссылок:
В обоих случаях, те интернет-документы, которые содержат в своем контенте исходящие ссылки на несуществующие или запрещенные страницы следует рассматривать как своего рода отклонение от корректно функционирующей системы и, по всей логике вещей, они не должны оказывать влияния на результаты поисковой выдачи. Все-таки основополагающий принцип Google PageRank состоит в том, что вес страницы рассчитывается исходя из ссылающихся на страницу документов, а не из тех особенностей (в данном контексте имеется в виду отдача 404 и 403 ошибок) соседей по сети, которые с нею связаны. В нашем распоряжении имеется неподтвержденная информация о том, что в современном интернете наблюдается тенденция к увеличению объема подобного рода умерших по причине своей неактуальности ссылок. Мы ознакомились с рядом исследований [2, 3], посвященных прогнозам полураспада URL-адресов на последующие 4-5 лет. В частности, [2] описывает процесс исчезновения в зоне .COM более 50% отслеживаемых web-страниц в первые 24 месяца. Более того, в процессе обхода более чем 1 млрд. документов мы обнаружили, что около 6% из них возвращают нам код 404, что натолкнуло нас на здравую мысль о том, что в перспективе проблема глобального учета подобного вида отмерших страниц будет только усугубляться. Вопрос увеличения доли битых страниц во многом перекликается с наблюдениями Najork и Wiener [4], выполнявших поиск в ширину и, соответственно, стремившихся найти наибольший ранг документа на раннем этапе обхода. Напомним, что суть данного обхода и разметки вершин веб-графа сводится к тому, что началу обхода приписывается метка 0, а смежным с ней вершинам — 1; после чего мы имеем возможность рассмотреть окружение 1-ой вершины и пометить окружающие ее узлы меткой 2, и т.д.
Если анализировать отсканированный нами 1,1 млрд. страниц, то мы обнаружим следующую картину: после значительного всплеска и незначительного затухания процента обнаруженных нами ссылок на несуществующие web-документы, их доля будет неуклонно расти по мере индексации веба. Причиной этому является то, что все большее количество страниц за время нашей работы утрачивало свою актуальность и выдавало 404 ошибку. Поскольку текущая работа обнаруживает наличие прямой корреляции между ссылками на несуществующие HTML-документы и снижением качества цитирующих их площадок, можно предположить то, что качественная оптимизация и продвижение сайтов должна ставить своей целью поддержание актуальной ссылочной структуры обслуживаемого веб-ресурса. В дальнейшем мы опишем вам некоторые поисковые алгоритмы, которые могут выполнять пессимизацию голосующей способности страниц сайтов, имеющих в своем содержимом ссылки на штрафные узлы. Мы надеемся, что учет подобного рода данных позволит нам улучшить качество персонального поиска и более эффективно управлять сайтами в процессе сканирования.
Рассмотрим теперь пример, при котором ссылки на штрафные узлы будут иметь для наших подсчетов существенное значение. На Рис. 15 показано 4 документа, один из которых является безисходным.
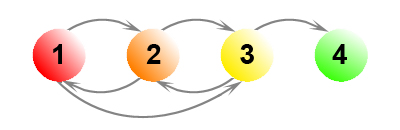
Если заниматься подсчетом Google PageRank с α= 0.85, то для трех сильно связанных документов и одной виртуальной страницы получаем:
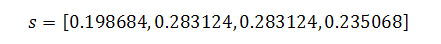
Если же мы сделаем допущение, что узел 3 имеет не одну, а четыре висячие ссылки, тогда наши новые веса составят:
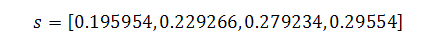
Как и следовало ожидать, голосующая способность виртуального узла 3 возросла, но одновременно с этим вес документа 2 существенно снизился. Таким образом, ссылки на документы, отдающие нам коды ошибок 404 и/или 403, могут оказывать значительное воздействие на своих ближайших соседей по всемирной паутине.
В данном блоке мы рассмотрим с вами несколько модификаций классического алгоритма PageRank, которые могут улучшить ранжирование документов, имеющих исходящие ссылки на штрафные страницы. В их число входят: алгоритм возврата, петельный алгоритм, переходы с весами и BHITS.
Суть данного метода заключается в том, что в случае наличия на какой-либо страницы исходящей мёртвой ссылки на штрафной документ, ее голосующая способность должна быть пропорционально разделена между имеющимися рабочими ссылками, а оставшееся (штрафное) значение возвращено тем страницам, которые вызвали увеличение ее ранга на этапе предыдущей итерации. В конце концов, мы достигаем эффекта ограничения притока голосующей способности на штрафные узлы со страниц наших web-сайтов. В уже известной нам модели случайного серфинга пользователя данная методика соответствовала бы попаданию пользователя на страницу без исходящих ссылок и его последующего возврата к нужным файлам посредством использования интернет-обозревателя (браузера). В качестве наглядного примера, описывающего нам алгоритм возврата, можем представить страницу i, которая ссылается на штрафной веб-документ p. Для xi имеем:
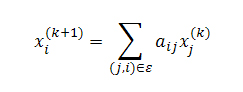
Мы хотим вернуть часть (скажем, βi, где 0<βi<1) голосующей способности тем интернет-страницам, которые указывают на наш штрафной документ (то есть такой j, где (j,i) ∈ E). Мы можем сделать это посредством изменения расчета PageRank таким образом, чтобы
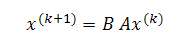
где B, как и А, представляют собой стохастическую матрицу, а сумма элементов в каждом столбце равна единице. То есть, eTB =eTA = eT. Мы полагаем, что оштрафованный голос i следует распределит между его донорами в пропорциях βiaij, оставляя нашей странице только часть (1-βi) первоначального целостного значения Google PageRank равного 1. В матричном выражении тот случай, когда мы возвращаем голос только одной странице-донору может быть представлен следующим образом:
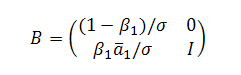
где a1T является первым столбцом матрицы А (за исключением а11), и:
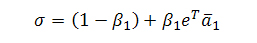
является таким нормализирующим коэффициентом, что В считается стохастической матрицей. Естественно, если голосующая способность возвращаются нескольким web-документам, мы распределяем общее значение PR в определенных соотношениях (1-βi) между донорами нашей странички. На практике, данная модификация известного алгоритма Google PageRank подразумевает дополнительный шаг не только на каждой его итерации, но и после умножения значения вектора В, хотя, стоит заметить, что вторая ситуация встречается достаточно редко. Если же заводить разговор о более конкретных примерах, то описанная выше операция может достаточно эффективно применяться к страницам, указывающим на те ресурсы, которые отдают 404 ошибку. Обозначим за gi число «хороших» исходящих ссылок со страницы i, а bi количество «плохих» (штрафных) линков. Тогда мы можем оштрафовать страницу i следующим образом:
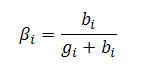
Если мы представим, что на нашем рисунке 15 имеется 8 исходящих ссылок с документа 3, из которых 4 отдают нам 404 ошибку (мертвые ссылки), а оставшиеся 4-ре признаются рабочими, то, посредством применения данного алгоритма, получаем уже новые значения PageRank (0.292287, 0.312162, 0.1666, 0.228948) для всех (3 и 1 виртуальный узел) наших интернет-страничек. Видим, что документ 3 имеет существенно меньшее (сниженное) значение голосующей способности по сравнению с его соседями 1 и 2. Здорово? Идем дальше.
Существует утверждение, что на каждом шаге наш пользователь может как проследовать по исходящей по ссылке с вероятностью α, так и перейти на какую-либо случайную страницу в сети с вероятностью 1-α. Петельный алгоритм заключается в том, что мы добавляем нашему документу ссылку на самого себя, тем самым, создавая ребро, инцидентное одной и тоже вершине. После того, как мы это сделали (предполагается, что все возможные петли до этого шага были заранее удалены с нашего графа), мы переходим по ней с вероятностью γi, которая будет менее значительной в том случае, если веб-документ имеет множество исходящих ссылок на штрафные странички. Таким образом, те сайты, которые не имеют в своем содержимом мёртвых линков, будут сохранять свой PR в случае нашего перехода по нашей петельной ссылке, а наличие хотя бы одной единственной ссылки на несуществующий файл будет снижать их первоначальную голосующую способность. Для расчета параметра γi нам необходимо выбрать вероятность γ и использовать формулу γi=γ⋅gi/bi+gi, где bi обозначается количество исходящих линков со страницы i к штрафным документам, а gi — тех ссылок, которые ведут к актуальным интернет-сайтам. Однако для того, чтобы наша матрица была стохастической, мы должны скорректировать вероятность телепортации с 1-α до 1-α-(γbi/bi+gi). В принципе, существует несколько моделей, описывающих работу данного алгоритма, в наиболее простой из которых мы просто добавляем на каждую хорошую страницу ссылку на саму себя и всякий раз осуществляем случайный переход по исходящим линкам (в том числе и по тем, на которые являются петлями) с равномерной вероятностью. Однако мы можем усложнить себе задачу таким образом, при котором параметр γi будет подбираться для каждой странички нашего сайта индивидуально, а также, помимо вероятности перехода нашего пользователя по петельному линку, добавим в нашу модель вероятность перехода 1-γi в соответствии с классической формулой Google PageRank. Несмотря на большое обилие всевозможных модификаций данного алгоритма, все они достигают своей основной цели — поток голосующей способности к штрафным сайтам ограничивается.
В предыдущей части мы уже занимались обработкой штрафных страниц (например, с кодами ответа HTTP 404 Not Found) на нашем графе под видом висячих узлов и минимизировали их воздействие (см. раздел «Обработка висячих страниц»), но в отличие от стандартной процедуры, которая предполагает последующее равномерное/выборочное перераспределение веса виртуального узла (n+1), мы предлагаем альтернативный механизм смещенного перераспределения, при котором оштрафованные документы получают меньшее значение голосующей способности. Для этого, используя приведенные выше обозначения для хороших и плохих документов, взвесим исходящие ссылки из виртуального узла к качественному документу в С (или ко всему набору) с коэффициентом p и к штрафному узлу с pgi /(gi + bi), где p подбирается таким образом, что сумма весов всех вершин нашего графа будет давать 1.
Ниже представлена модификация классического алгоритма HITS [5], которая является производной от случайного блуждания пользователя как в прямом, так и обратном направлении, однако, наряду с этим, основными его отличительными характеристиками от более известного прототипа является то, что работа BHITS осуществляется вне зависимости от запросов и рангов интернет-документов. В этом смысле он больше напоминает методологию описанную SALSA [6] или в [7], но суть его, как и во всех описанных ранее алгоритмах, заключается в некотором снижении голосующей способности тех web-документов, которые цитируют штрафные сайты. Соответственно случайному серфингу нашего пользователя, каждый последующий шаг вперед будет рассчитываться в нашем случае по аналогии с PR, а в случае попадания на висячий узел мы будем вынуждены вернуться назад. Важно отметить, что возврат на невисячем узле обеспечивается в нашей модели посредством петельного линка, а процедура возвращения с висячего разделяется на два типа. Для первого из них мы будем передавать свой голос виртуальному узлу (справедливо для попадания на штрафной документ), а для второго типа, который учитывает нештрафной ресурс, — равномерно распределять текущую оценку страницы между всеми обратными ссылками. Мы полагаем, что все сайты представляет собой связанные между собой цифровые документы, что, безусловно, подтверждается нашими сканнерами, однако нам также следует предположить, что нашим роботам-индексаторам известны все внутренние ссылки, связывающие данный набор разрозненных интернет-страниц, поскольку в противном случае алгоритм не сможет быть запущен. Поэтому, мы будем учитывать только сильные связи, и любая страница без входящих ссылок будет расцениваться в рамках поставленной перед нами задачи как штрафная. Взамен операции возвращения по входящим на них ребрам, как и в классической модели PR, будем применять случайную телепортацию на любое множество документов в сети. Результатом этого процесса становится как «возврат» голосующей способности тем сайтам, которые цитируют из своего контента нештрафные странички, так и перераспределение рангов, присваиваемых некачественным web-узлам. Если матрицу, описывающую PageRank марковского процесса, обозначить за Р, тогда матрица для алгоритма BHITS обозначается как BP, в которой B есть ни что иное, как матрица кодирующая обратный шаг пользователя. С учетом того, что штрафные страницы, как правило, оказываются в самом конце поисковой выдачи, то давайте обозначим полустепень захода узла j через δ(j), а вероятность перехода нашего пользователя с j на i через bij = 1/δ(j). Тогда, для описания обратного шага мы получим следующую матрицу:
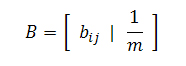
BP является матрицей переходных вероятностей для цепи Маркова по той простой причине, что она является продуктом двух прочих стохастических матриц. Эта марковская цепь будет создавать стационарное распределение вероятностей, то есть такое распределение, которое не будет меняться с течением времени, но вполне очевиден тот факт, что для тех веб-документов, которые ссылаются на штрафные сайты/страницы, вероятность будет меньшей, нежели чем в стандартном алгоритме Google PR.
Учитывая все возрастающий объем глобальной сети, проблема эффективного практического внедрения любого алгоритма ранжирования является достаточно существенной. Первая тройка описанных выше алгоритмов, которые основываются на модификации классической модели Google PageRank, а если говорить более конкретно, на изменениях матрицы А, не потребует от нас значительных вычислительных затрат. Почему? Дело в том, что все эти дополнения по своей сути носят локальный характер и, кроме соблюдения требований нормализированности матрицы, изменения записей в i-строке будут зависеть только от количества штрафных и хороших исходящих ссылок из i-го узла, bi и gi. Отсюда, у нас появляется возможность не только предварительно вычислять модифицированные матрицы за линейное время (вектор b и g), но и вносить все необходимые изменения в процессе наших итераций. Четвертый алгоритм BHITS представляется для практического внедрения куда более сложным, и основная его проблема заключается в том, что он требует учёта всех существующих в интернете висячих узлов. Вспомнив же, что в ходе нашей исследовательской работы нами было проиндексировано только 1 из 5 млрд. HTML-страниц (думается, что число висячих узлов в пять раз превышает обнаруженный нами объем), сделаем логичный вывод о том, что такой подход явно не подходит для крупномасштабной реализации и нам следует использовать методологию, базирующуюся на PageRank.
До текущего момента мы в основном затрагивали висячие узлы, игнорируя прочие особенности веба, которые также могут быть учтены при подсчете PR документов. Оригинальная парадигма данного алгоритма моделировала сеть как некоторый набор страничек, по которым пользователь может перемещаться как посредством прохождения по ссылкам, так и телепортируясь на случайные узлы по причине утрата интереса к существующим и/или для выхода на сайты прочих тематик. Безусловно, она была достаточно упрощенной и не могла отразить реального пользовательского поведения в полном смысле этого слова, в частности можно сослаться на то, что пользователь не может осуществлять равномерный случайный выбор документов или даже быть осведомленным в доступном для него наборе URL-адресов. Ряд недавних исследований предполагает, что подавляющий процент пользовательских сессий начинается с обращения к поисковым системам, далее идет сам вопрос и следование по предложенным ссылкам на странице поисковой выдачи. Продолжительность сессии складывается из прохождения по ссылкам на оригинальный веб-документ и ознакомления с его содержимым, возможного возвращения к странице результатов и/или переформулировки запроса до тех пор, пока у пользователя поисковой машины сохраняется потребность в получении необходимой ему информации. Однако в случае начала новой сессии, пользователь уже не обращается к случайному узлу, а возвращается к поисковой машине для формулирования очередного запроса и именно это поведение исключается в классической парадигме Google PageRank, особенно в той части, что в пользовательском перемещении был заложен неоднородный по своему распределению набор всевозможных узлов.
Еще одной вариацией на тему модели интернет серфинга, несколько позже положенного в классический PageRank, является то, что пользователь выбирает для своего случайного перехода страницу из ряда трастовых узлов, в принципе это то, о чем мы писали в части алгоритма доверия Google TrustRank. Впоследствии, данная схема была использована как средство для увеличения персонализирующей составляющей (алгоритм Topic-Sensitive PageRank [1]) поискового механизма Google. Согласимся, что это было бы эффективной моделью для тех пользователей, которые осуществляют свое перемещение к каким-либо URL-адресам из набора имеющихся в их браузере закладок или являются частью аудитории крупных интернет-порталов. Однако в случае с теми же самыми порталами мы будем иметь неравномерное распределение рандомных перемещений, поскольку такие интернет-ресурсы очень быстро меняют свое содержимое и генерируют огромное число новых ссылок в краткий период времени, которых с момента последнего визита пользователя просто не существовало! В [8] отмечается, что вероятностные значения, присваиваемые алгоритмом PageRank распадаются в соответствии со степенным законом распределения вероятностей, и это необходимо учитывать в модели развивающегося веба. Ими было предположено, что телепортация осуществляется равномерно на случайно избираемую страничку.
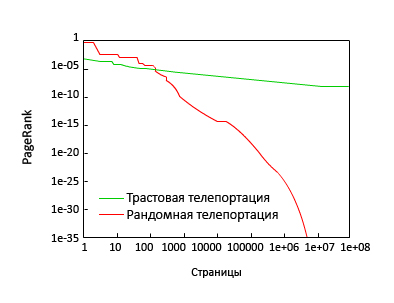
На Рис. 16 показано распределение значений PR, вычисленного посредством трастовой и рандомной телепортации (0.5) к одному из авторитетных сайтов (microsoft.com и yahoo.com). И хотя наши наблюдения во многом подтверждают данные [8], мы видим, что стратегия телепортации оказывает глубокое влияние на гипотетическое распределение вероятностей для попадания пользователей на страницу сайта. В частности, если ссылочная структура веба была бы иерархической, в которой каждая предыдущая страница, связанная с последующей, тогда бы распределение уменьшалось экспоненциально с продвижением вглубь иерархии, а окончание (кривой) распределения показывало бы результаты более близкие к экспоненциальному, нежели чем к степенному закону распределения. Попутно заметим, что было бы очень заманчиво предлагать пользователям перемещаться по страницам на основании присваиваемых им значений PR.
Одним из предположений, сделанных в оригинальной работе Lawrence Page и Sergey Brin [9] было случайное перемещение к цифровым документам верхнего уровня страниц сайта, что во многом увязывается с нашей склонностью восприятия информации, построенной по иерархическому принципу. Кроме того, исходя из отсканированных нами страниц мы обнаружили, что 62,4% проиндексированных ссылок оказались внутренними, а оставшиеся исходящие линки, как правило, вели на главные страницы веб-сайтов (см. Табл. 2)
| Глубина | Доля |
| 0 | 0.75 |
| 1 | 0.089 |
| 2 | 0.035 |
| 3 | 0.017 |
| 4 | 0.005 |
| 5 | 0.002 |
| 6 | 0.001 |
Данные структурные особенности веба показывают нам очень высокий уровень компрессии для графа хостов и позволяют использовать блок-ориентированный подход для ускорения сходимости Google PageRank. С учетом иерархической структуры самих сайтов, а также того факта, что в качестве источника цитирования вебмастера предпочитают ставить обратную ссылку не на какую-либо внутреннюю страницу сайта, а именно на главную, мы считаем необходимым исследовать страницы интернет-сайтов как элементы единого организма, а также присваивать им ранговые значения, исходя из информационной ценности. Для данных расчетов используется алгоритм HostRank. Говоря более формально, в том случае, если имеется такой URL на хосте S, которой ссылается на URL хоста D (имена хостов представляют собой узлы на нашем графе), то мы строим между ними ориентированное ребро. Помимо этого, мы можем назначить ребрам между хостами некоторые весовые значения (в сумме они будут давать нам единицу), которые отразят нам количество ссылок с URL-источника к URL-цели. Затем, в первоначальном подсчете PR заменим этими весами элементы aij = 1/dj. Несмотря на то, что включение реберных весов потребует от нас дополнительной информации для каждого ребра данного графа, они могут улучшить качество тех поисковых результатов, которые отражают сильные связи.
В качестве альтернативы мы могли бы использовать веса, состоящие из числа обособленных URL-целей. По той простой причине, что мы имеем дело с малыми графами (в нашей выборке имелось около 48 млн. хостов, хотя многие из них не были проиндексированы по разным причинам), вычисление HostRank оказывается существенно простой задачей нежели чем самого Google PageRank, а следовательно он может быть объединен с другими оптимизационными подходами, опирающиеся на более сложные алгоритмы линейной алгебры; быть более эффективным, чем диспетчеризация ввода/вывода (I/O) и аппроксимаций, использующих только локальную информацию.
Страница материала:
Детекция поискового спама. Часть 1: Введение в алгоритм Google TrustRank
Детекция поискового спама. Часть 2: Расчет алгоритма Google TrustRank
Детекция поискового спама. Часть 3: От TrustRank к алгоритмам HostRank и DirRank
Детекция поискового спама. Часть 4: HostRank или PageRank, вычисляемый по графу хостов
Детекция поискового спама. Часть 5: От DirRank к алгоритму Truncated PageRank
Детекция поискового спама. Часть 6: Truncated PageRank и Вероятностный Подсчет
Детекция поискового спама. Часть 7: Знакомство с алгоритмом BadRank, обнуляющим Google PageRank
Детекция поискового спама. Часть 8: Google BadRank и ParentPenalty
Детекция поискового спама. Часть 9. Введение в алгоритм SpamRank
Детекция поискового спама. Часть 10: От исследования SpamRank к алгоритму Anti-TrustRank
Детекция поискового спама. Часть 11: Эксперименты с алгоритмом недоверия Anti-TrustRank
Детекция поискового спама. Часть 12: Применение принципов термодиффузионной
Детекция поискового спама. Часть 13: Детальный анализ алгоритма ранжирования DiffusionRank
Детекция поискового спама. Часть 14: Вычисление AIR на веб-графе, эквивалентного электронной схеме
Детекция поискового спама. Часть 15: Применение искусственных нейронных сетей
Полезная информация по продвижению сайтов:
Перейти ко всей информации