Ранжирование страниц c использованием алгоритма прогнозирования структуры веб-графа

Аннотация

Алгоритм ссылочного ранжирования интернет-документов Google PageRank является одним из самых популярных методов ранжирования страниц, именно на парадигме данного алгоритма построены практически все без исключения методологии ссылочного учета, в том числе и тематический Индекс Цитирования Яндекса, который представляется не более чем одной из его многочисленных модификаций — ведется расчет по хостам / директориям (по аналогии с HostRank / DirRank [1]) с учетом их тематической составляющей. Однако по мере увеличения объема глобального веба, обход всех доступных для сканирования документов, в том числе и акселерация PR, становится все более трудоемкой задачей. В результате чего, значение PageRank на текущем этапе рассчитывается только по компонентам двусвязанности веб-графа. Это дает несколько неточные результаты из-за наличествующей неполноты всех данных, которое, в свою очередь, является следствием присутствия в наших расчетах так называемых «висячих узлов». Для преодоления дефицита информации мы предлагаем вам ознакомиться с принципиально новым вариантом классического алгоритма Google — PreRank, который прогнозирует структуру веб-графа. Здесь различные классы висячих страниц (dangling pages) подвергаются индивидуальному анализу таким образом, который позволял бы нам прогнозировать структуру веб-графа с большей аккуратностью. В настоящем материале мы детально описываем шаги нашего алгоритма. Более того, экспериментальные данные показывают, что данный метод позволяет достичь достаточно обнадеживающих результатов по сравнению с теми методами, где использовалась блочная структура.

1. Введение

Алгоритм Google PageRank является крайне эффективным методом ранжирования веб-страниц, однако лишь в том случае, если мы рассматриваем веб как статичную структуру, не предполагающей своего эволюционного развития. Вследствие этого объективного процесса, то есть возросшего объема документов, находящихся в индексе поисковой машины; динамики, ограничения пропускной способности, необходимо признать, что его точность неуклонно стремится к нулю. Следовательно, ранг страницы сегодня рассчитывается исходя из компонент двусвязанности. Конечно, это представляется более эффективным подходом, нежели чем осуществлять графоориентированные расчеты посредством таких моделей, как, например, «бабочка», которая была обнаружена в ходе сканирования более 200 млн. веб-узлов в 1999 году, и содержала три большие компоненты: центральное сильно связанное ядро (SCC), состоящее из 56 млн. узлов, а также заходящий (IN) и исходящий (OUT) подграф по 44 млн. узлов в каждом. Помимо них, в структуре «бабочка» были зафиксированы относительно изолированные отростки и несвязанные компоненты [4]. В любом случае это приводит к ошибочным результатам, которые незамедлительно отражаются на качестве поисковой выдачи, заставляя поисковые системы нервничать и искать новые способы по устранению этой проблемы, модифицировать свои алгоритмы и т.д.

Итак, возможно ли повысить аккуратность PR? В настоящем материале, мы предлагаем решение, заключающееся разработке новой модели ранжирования (PreRank), прогнозирующей и более точно оценивающей структуру веб-графа, что незамедлительно приведет нас к более точным оценкам, присваиваемых Google PR. В классической работе [3] PR присваивает относительную важность цифровым документам на основании ссылочного веб-графа. Google PageRank, вычисляется по графу хостов в работе [1]; здесь нам дается ориентированный веб-граф G = (V, E), в котором голосующая способность (ранг) x_i всякой страницы i ∈ V рекурсивно определяется голосующей способностью ссылающихся на нее документов:

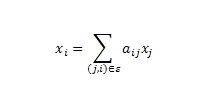
В матричном выражении данная формула принимает вид: x = Аx. Существует три типа страниц, которые могут быть обнаружены сканером поисковой системы в ходе обхода ссылочного веб-графа. К первому типу относятся новые документы или те, в ходе обращения к которым имела место ошибка; второй тип включает в себя документы без исходящих линков; третий тип документов предполагает по крайней мере одну исходящую ссылку. В модели веб-графа, представленной в [3] рассматривается только третий тип цифровых документов — там мы имеем максимальный подграф, который не имеет разделяющих вершин (шарниров), иными словами, мы пытаемся анализировать его в виде блока или компоненты двусвязанности. В то же самое время, первый и второй (висячие узлы) тип страниц рассчитываются в ходе последней итерации алгоритма. В работах [2] и [1] все три типа документов учитываются в моделях веб-графов, однако при этом первые два типа объединяются в единое целое, что с нашей точки зрения должно быть подвергнуто критике. Именно в ходе последующего статистического анализа мы обнаружим, что таким способом можно достичь большей аккуратности в присваиваемых алгоритмом оценках, а следовательно и улучшить качество поиска. Отметим, что наличие в индексе поисковой машины висячих узлов может оказывать существенное воздействие на ранги страниц с исходящими ссылками. В [1] они обрабатываются посредством добавления виртуальной страницы таким образом, что вычисление оказывается эффективным, но наша модель отличается от всех вышеупомянутых тем, что она обладает прогнозирующей способностью.

2. Модель алгоритма PreRank

Несмотря на то, что произвести точную оценку ссылочной структуры в целом достаточно сложно, некоторые элементарные оценки представляются для нас вполне осуществимыми. Мы можем оценить полустепень захода всякой страницы (то есть количество входящих ссылок) и, таким образом, получить некоторую статистическую информацию о ссылочной структуре. Основным положением в алгоритме PreRank является то, что по мере увеличения объема информации о структуре веба, мы автоматически увеличиваем точность всех наших последующих умозаключений. Выделим в модели нашего алгоритма PreRank следующие шесть шагов:

Шаг 1. Разделим множество страниц V графа (|V| = n) на три подмножества: S, D¹, и D², где S (|S| = m) обозначает подмножество страниц третьего типа; D¹ (|D¹| = m₁) — подмножество страниц второго типа, а D² (|D²| = n − m − m₁) обозначает набор, состоящий из документов первого типа.

Шаг 2. Прогнозируем полустепень захода d⁻(v_i) по количеству обнаруженных линков fd⁻(v_i) из посещенных страниц к документу v_i. Используя метод поиска в ширину, мы предполагаем, что число найденных ссылок fd⁻(v_i) из посещенных страниц к документу v_i пропорционально реальному количеству линков со всех страниц множества V к документу v_i; следовательно, d⁻(v_i) ≈ n/(m + m₁) • fd⁻(v_i). Эта предположение имеет смысл, и сейчас мы это поясним. Вопреки тому обстоятельству, что обход веб-графа агентом накопления данных начинается с заданного интернет-сайта ко всем прочим ресурсам определенным образом, логично предположить, что его способность обнаружить линк на нашу интернет-страничку v_i будет зависеть от плотности ссылочного графа, и которую в данном случае мы обозначим равной d⁻(v_i)/n. Поскольку наш краулер смог обнаружить fd⁻(v_i) подобного рода ссылок со страниц m, то fd⁻(v_i)/(m+m₁) является приблизительной оценкой плотности. Далее, мы получаем вышеуказанную оценку.

Шаг 3. Вычислим матрицу А. Все ссылки (fd⁻(v_i)) исходят со страниц, содержащихся в подмножестве S, а остальные ( d⁻(v_i)− fd⁻(v_i)) с документов, содержащихся в подмножестве D² (цитирование из подмножества D1 полагается как невозможное). Без какой-либо предварительной информации о распределении этих оставшихся линков, мы полагаем, что оно будет неравномерным по всем документам в подмножестве D², ссылающихся на страницу v_i, то есть все оставшиеся ссылки являются общими для всех документов в подмножестве D². Таким образом, матрица А, моделирующая поведение пользователя в соответствии с актуальной ссылочной структурой, рассчитывается как:

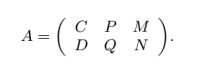
C и D используются для моделирования известной ссылочной структуры из подмножества S к множеству V в [3], где cij в C и dij в D обозначается как 1/d_j в том случае, если имеется ссылка j к i; в противном случае 0. Далее, d_j является полустепенью исхода страницы j; M и N, моделирующие ссылочную структуру из подмножества D² к множеству V, обозначаются как: (MN)^T = diag{l₁, … , l_n}, где l_i =(d⁻(vi) − fd⁻(v_i))/m₂∑. Параметр m₂ используется для равномерного распределения оставшихся входящих ссылок d⁻(v_i) − fd⁻(v_i) между всеми документами в D², а  ∑ = ∑ⁿ_i=1 d⁻(v_i) − fd⁻(v_i) умножается на знаменатель для того, чтобы наша матрица была стохастической. P и Q, моделирующие ссылочную структуру из подмножества D¹ к множеству V, определяем на шаге 5.

Шаг 4. Моделируем операцию пользовательской телепортации. Положим, что наши с вами пользователи, отказавшиеся следовать по актуальной ссылочной структуре, будут совершать прыжки к документу v_i с вероятностью f_i. Тогда, матрицей, моделирующая операцию телепортации, является fe^T. Обозначим вектор (f₁, f₂, … , f_n)^T за f. Предшествующие предложения включали в себя выбор равномерного распределения среди всех интернет-страниц, трастовых наборов документов; равномерного распределения среди множества высокоранжируемых страниц или по персонализированному набору предпочитаемых документов.

Шаг 5. Пусть (PQ)^T = diag{f₁, … , f_n}1_n×m1 Когда пользователь столкнется со страницей второго типа, не имеющей исходящих линков по которым он смог бы проследовать далее, мы предполагаем ту же самую операцию телепортации, что была описана нами на Шаге 4.

Шаг 6. Ранг x_i должен удовлетворять x = [(1 − α)fe^T + αA]x, где α является вероятностью прохождения по актуальной исходящей ссылке, а 1 − α — вероятность совершения «случайного прыжка».

Представленная выше модель и называется алгоритм прогнозирования ссылочной структуры (Predictive Ranking). В отличие от [1,2], здесь мы, во-первых, имеем разложение матрицы А, а во-вторых, (M N)^T строится на основании полученных прогнозов. Именно это и дает нам более аккуратную оценку ссылочной структуры и, как следствие, более точный результат.

3. Эксперименты

Для наших экспериментов мы выбрали относительно небольшой подграф (домен cuhk.edu.hk) по той простой причине, что в этом случае мы смогли бы получить относительно полную структуру вершин и, следовательно, рассчитать относительно точные значения рангов страниц для упрощения последующего сравнения результатов. Поскольку оценка авторитетности той или иной странички в интернете по своей имманентной природе является субъективной, сравнение алгоритмов ссылочного анализа всегда представляется достаточно трудоемкой задачей. Однако мы разработали новые методы сравнения, заключающиеся в подсчете разницы между предыдущими результатами, которые были получены ранее, и окончательными, которые, соответственно, являются уже относительно точными. Если говорить более конкретно, мы используем мгновенные снимки (SnapShots) 11 матриц в процессе обхода нашим веб-краулером всех вершин из имеющегося в нашем распоряжении множества страниц, а именно, A₁, … , A₁₁. Количество успешно отсканированных документов и общее их число обнаруженных в исключительно на 11 момент составило 502,610 и 607,170 соответственно. С 1 по 10 моменты их число было следующим: 7712, 18542; 78662, 120970;109383, 157196; 160019, 234701; 252522, 355720; 301701, 404728; 373579, 476961; 411724, 515534; 444974, 549162; 471684, 576139.

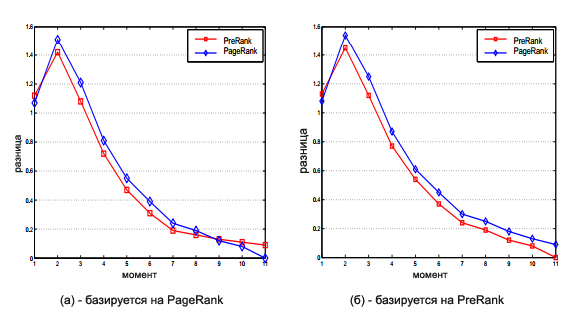
Применяя алгоритм PreRank и модифицированный Google PageRank из [2] к этим 11 наборам данным, мы получаем результативные ранговые значения PreR[t] и PR[t](t = 1, 2, … ,11). Коэффициент α = 0.85; для обоих алгоритмов используется равномерное распределение (вектор f). Разница D1[t] между PreR[t] and PR[11]определяется как ||PreR[t]−Cut(t, PR[11])/Sum[t]||₁; аналогично рассчитывается разница D2[t] между PR[t] и PR[11]. Результаты D1[t] и D2[t] отображены на Рис. 1 (а). На момент 1, набор данных еще слишком мал для того, чтобы иногда дать точную статистическую оценку, поэтому PR[1] ближе к окончательному результату, чем PreR[1] к PR[11]. Но в диапазоне 2 -8 PR[t] дает более точную оценку и PreR[t] оказывается ближе, чем PR[t] к итоговому PR[11]. Как мы и ожидали, по мере приближения к концу (11), PR[t] снова становится ближе к PR[11], нежели, чем последующие результаты PreR[i]. Это связывается с тем, что PR[11] используется нами в качестве эталонного образца в текущем сравнении и, надо сказать, что такое обстоятельство может вызвать ряд предубеждений касательно методологии PreR[t]. Несмотря на это, в 7 из 11 (63%) случаев PreR[i] оказывается ближе к последнему PR в итоговом результате PR[11]. Несмотря на это, в 7 из 11 (63%) случаев PreR[i] оказывается ближе к окончательному PR в итоговом результате PR[11]. Если в качестве эталонного образца сравнений используем PreR[11], во всякий момент отличный от 1-го, то есть в 91% случаев, PreR[t] представляется наиболее близстоящим к PreR[11], чем PR[t]. Данные представлены на Рис. 1 (б)

4. Заключение и благодарности

Итак, результаты, которые были достигнуты с помощью алгоритма PreRank являются наиболее точными (ближе всего отстоящие от окончательного результата), нежели чем те, что продемонстрировал модифицированный алгоритм PR. Даже когда мы использовали PageRank в качестве эталона (некоторые данные предубеждали против нашей модели), при взятии PreRank в качестве стандарта полученая точность оказалась неоспоримой, в отличие от противостоящей нам модели Google PR. Мы выражаем огромную благодарность Mr. Patrick Lau за его ценный вклад в наши практические эксперименты. Данная работа была выполнена при поддержке Research Grants Councils of the HKSAR, Китай (гранты CUHK4205/04E и CUHK4351/02E).