SEO-Константа
Яндекс.Директ + оптимизация
Алгоритмы категоризации веб-страниц долгое время отодвигались на второй план в сравнении с алгоритмами классификации по методу ключевых слов, поэтому результаты применения этих алгоритмов пока еще плохо изучены. На данный момент некоторые алгоритмы категоризации вроде строкового ядра нашли свое применение скорее в биоинформатике, чем в веб-программировании, что обусловлено их невысокой производительностью, если рассматривать её в стандартах требований интернет-систем. При этом проведенные исследования показали, что должная оптимизация способна устранить большую часть недостатков алгоритмов категоризации, тем самым повышая их эффективность касательно их применения для языков со сложной морфологией и грамматикой. Данная статья содержит один из примеров подобной оптимизации, а так же примеры двух классификаторов, которые можно использовать для их реализации. Результаты, которые были получены во время тестов, доказывают, что дальнейшее изучение проблемы сможет устранить остальные недостатки подобных алгоритмов.
Задачу классификации можно упростить и свести к нахождению правила, согласно которому на основе некоторых наблюдаемых признаков, свойственных тому или иному объекту, сам объект можно отнести к одному из заданных классов. В целях упрощения задачи постановим, что существует только два класса, из этого следует, что задачу можно сформулировать следующим образом:
Зададим пространство X=RN и множество классов Y={-1; +1}. Неизвестное распределение P(x, y) будет разделять множество точек в пространстве X на два класса. Тренировочное множество T={(x, y): x ∈ X, y ∈ Y} включает в себя пары, которые независимо распределены (i.i.d) с распределением P. Таким образом, тренировочное множество T содержит примеры классификации, то есть, реализации случайной величины (x, y). Задача, таким образом, сводится к нахождению функции f: RN→{-1; +1}, которая будет правильно классифицировать точки из пространства X по примеру тестового множества.
В поставленных условиях лучшим решением будет функция f, которая сводит к минимуму средний риск классификации:
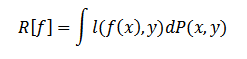
где l является функцией потерь, к примеру l = (f(x)-y)2.
Прямая минимизация данного интеграла невозможна, так как используется неизвестное распределение P. Именно поэтому обязательным считается поиск функции f, которая ближе всех к оптимальной согласно имеющейся информации, т.е. тренировочного множества и свойств класса функций, из которых и выбирается функция f.
Второй проблемой является тот факт, что некоторые из подлежащих классификации объектов не принадлежат множеству RN, поэтому второй задачей является сопоставление объектов с определенными точками во множестве RN посредством определения признаков. Признаки здесь являются основным определяющим фактором, позволяющим различать отдельные объекты и впоследствии их классифицировать. Именно поэтому выявление признаков в задачах классификации текстовых документов, к которым относятся веб-страницы, эта задача вынесена на первый план.
Одним из оптимальных методов классификации является классический метод ключевых слов, которые характеризуют текстовой документ. Этот метод используется большинством существующих поисковых систем в области классификации документов. Согласно методу ключевых слов, текстовой документ здесь представляется вектором, частоты появления ключевых слов в которых являются его компонентами. Этот метод считается одним из самых эффективных, но при этом, само собой, обладает и некоторыми недостатками:
Конечно, метод ключевых слов претерпел множество модификаций и изменений, которые позволили устранить часть существующих недостатков, но полного их устранения добиться не удалось. Так, например, метод групп ключевых слов в контексте позволяет с определенной долей точности справиться с зависимостью смысла слова от контекста, однако такие проблемы, как морфологические изменения слова и банальная неграмотность, по сути, являются неразрешимыми проблемами.
Когда решена задача выявления признаков, применить можно один из стандартных методов классификации, примерами которых могут послужить нейронные сети и деревья решений [4]. Подобные методы в своей основе используют отделение точек разных классов друг от друга, оперируя их векторами в пространстве признаков Rn (или же в преобразованном пространстве, примером которого может послужить спрямляющее пространство скрытого слоя нейронной сети). При этом классические алгоритмы обладают всеми недостатками, приобретенными на предыдущем этапе.
В теории машинного обучения сегодня все чаще используются иные подходы, которые основаны не на явном извлечении признаков, а на использовании ядер. Множество X в нашем определении будет включать в себя все исходные объекты. Примем за Ф отображение, которое действует из X в F, при этом за F принимаем пространство, где образы исходных объектов линейно-отделимы (по сути Ф является аналогом функции выделения признаков). В этом случае функция k(x,y) будет ядром, если выполняется условие (Ф(x), Ф(y)) = (k, y). За ядро здесь принимается функция, которая берет два аргумента из множества исходных объектов и вычисляет скалярное произведение их образов в другом пространстве. Размерность F должна быть велика, так как от этого зависит линейная отделимость. Если пространство X линейно, то размерность F может оказаться больше, чем размерность X. Именно поэтому задача поиска разделяющей гиперплоскости в пространстве F может оказаться попросту невозможной. При этом, с учетом возможности записи алгоритма классификации только в терминах скалярного произведения, применение так называемых ядер и решение поставленной задачи возможно в условиях ограниченности ресурсов. Отображение Ф, которое необходимо для выделения признаков, напрямую не применяется.
На данный момент существует всего лишь несколько алгоритмов, которые могут быть оптимизированы для применения с функциями ядер, среди которых Метод Поддерживающих Векторов (SVM, Support Vector Machines, [2, [9], [11] и др.), Персептрон (Perceptron), Метод Ближайшего Соседа(Nearest Neighbor), Анализ Главных Компонентов (PCA, Principal Components Analysis, [4])и прочие. Все вместе они создают класс алгоритмов, которые основаны на ядрах (Kernel Machines, [4]). В таких задачах, как кластеризация и регрессия, каждый из этих методов наиболее точно отвечает специфическим условиям. Самыми удачными в рамках выполнения задачи классификации сегодня признаётся метод Large Margin Classifiers (SVM [2, 5, 11], Perceptron [22]).
Решение поставленной ранее задачи классификации, с учетом всего вышесказанного, требует выполнения трех условий:
В нашей работе использоваться для классификации будут только алгоритмы SVM[2, 5, 11] и Voted Perceptron[22] в комбинации с ядром SSK[3, 8].
Строковые ядра, использование которых обсуждалось выше, для своей работы не требуют разбора текста на отдельные составляющие, и именно поэтому удается решить проблемы, так или иначе связанные с синтаксисом языка и зашумленностью веб-страниц. Основных недостатком метода строковых ядер является их высокая вычислительная сложность, что приводит к отсутствию возможности повсеместного их использования. Конечно, для английского языка, который отличается не только большей простотой по сравнению с русским, но и с большей грамотностью его носителей, их использовать можно, поэтому в англоязычной сфере ранее не производилось сколь-либо глубоких исследований способов оптимизации метода строковых ядер, которые могут стать новым словом в разработке веб-приложений.
Принимая во внимание всё вышесказанное, можно с уверенностью заявить, что в основе единого простого и эффективного классификатора должен лежать метод строковых ядер, и целью данной работы является доказательство этого утверждения. В работе будет рассмотрено несколько способов снижения вычислительной сложности метода, сокращение количества вызовов ядра упрощением алгоритма работы классификаторы и рассмотрение условий, необходимых для возможности ведения параллельных вычислений. Наше исследование так же будет содержать несколько способов применения Voted Perceptron на ядрах SSK, сочетание которых может оправдать общий принцип, ведь сложность SSKздесь будет компенсироваться меньшим количеством вызовов строкового ядра, чем в случае с SVM. Предложенный классификатор, конечно, будет немного уступать в точности, но при этом будет применим к достаточно крупным объемам данных, с которыми приходится работать веб-приложениям. Кроме того, голосующий персептрон легко адаптируется к задачам многоклассовой классификации.
Здесь мы будем рассматривать стандартную задачу по классификации в пространстве Rn, где представлены два класса предположительно линейно-отделимых объектов. Здесь в качестве уравнения разделяющей гиперплоскости может использоваться следующая формула: (w, x) + b = 0, где за wпринимается нормаль к гиперплоскости. Образуемые при помощи данной гиперплоскости полупространства выражаются неравенствами (w, x) + b > 0 и (w, x) +b < 0, из чего следует, что все точки первого класса характеризуются правильностью первого неравенства, а для второго класса верно второе неравенство, поэтому решающая функция принимает следующий вид:
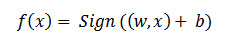
Подобных гиперплоскостей одновременно может существовать бесконечное множество, поэтому для определения нужной гиперплоскости необходимо прибегнуть к оценке риска классификации. Согласно доказанной В.Н.Вапником теореме [2], можно принять, что риск классификации оценивается в терминах эмпирического риска, установленного по тренировочным данным, и слагаемого, которое должно учитывать сложность класса функций, поэтому:
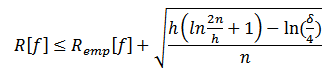
причем за h принимается VC-размерность для рассматриваемого класса функций, а вероятность выполнения неравенства p > 1 – δ.
В [4] демонстрируется эквивалентность минимизации риска классификации решению этой квадратичной задачи:
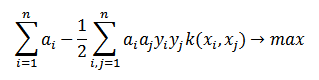
где 0 ≤ ai ≤ C, а i = 1,…, n и
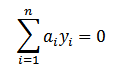
Принимая во внимание огромное количество проиндексированных веб-страниц, в качестве размеров обучающей выборки следует использовать порядка нескольких сотен тысяч примеров, что влечет за собой исключение стандартных численных методов квадратичного программирования (например, прямодейственные методы внутренней точки [14] и метод Ньютона) из рекомендованных к применению.
В последнее время было предложено несколько способов (алгоритмов [6], [7]), позволяющих полностью или частично решить данную проблему. Так, например, один из предложенных алгоритмов в своей основе имеет предположение, что исключение строк и столбцов, которые соответствуют нулевым множествам Лангранжа, из матрицы не отразится на решении задачи. Другой алгоритм предполагает решение задачи через решение подзадач с фиксированным размером, при этом двигаясь в направлении наибольшего спуска целевой функции. Задача оптимизации при обучении SVM здесь предполагает использование уже известного метода SMO (Sequential Minimal Optimization [7]).
Отличие, которое позволяет назвать метод SMO наиболее эффективным в рамках поставленной задачи, заключается в использовании принципа поочередного решения минимальных подзадач на каждом шаге обучения. Так как каждая задача включает в себя линейное ограничение, то и минимальное количество множителей Лангранжа для комбинированной оптимизации равняется двум. При этом задача для двух множителей решается аналитическими методами, не требуя при этом использования численных методов квадратичного программирования. Каждая из задач решается быстро и легко, поэтому общее их количество, которое довольно велико, уходит на второй план, т.е., общее решение находится быстрее. Еще одним преимуществом данного подхода является отсутствие необходимости хранения даже части Гессиана в памяти. Вышеизложенное позволяет сделать вывод, что метод SMO подходит для задач оптимизации при обучении SVM.
Решение задачи многоклассовой классификации позволяет использовать несколько подходов. Принятый стандартным подход предполагает поочередное решение бинарных задач: отделение сначала первого класса от прочих, далее второго и т.д, а также выделение каждого класса из всего множества. Результатом решения бинарных задач становится несколько обученных SVM для каждого класса объектов, причем при определении класса вновь введенного объекта каждая SVM возвращает коэффициент принадлежности, таким образом, класс определяется на основе максимального значения этого коэффициента.
pКак известно, метод, основанный на наборе ключевых слов, используемых как признаки класса, вызывает возникновение различных затруднений при его использовании.
Именно поэтому применение строковых ядер является одной из наиболее достойных альтернатив явному извлечению признаков. Основная идея SSK предполагает сравнение текстов по общему количеству содержащихся подстрок. С увеличением количества подстрок, содержащихся в двух текстах, возрастает степень схожести двух текстов, при этом неразрывность подстрок не является обязательным для сходства условием, а степень их разреженности определяет вес, с которым они включаются в скалярное произведение.
Стандартные обозначения, принятые в работе:
Введя эти условные обозначения, можно приступить к вычислению пространства признаков F и ядра k. Необходимо зафиксировать любое небольшое число n (в нашем примере будет использоваться 7). В качестве размерностей (т.е. осей координат) в пространстве признаков будут выступать все строчки с длиной n: F=R|∑|n. В этом случае, если t – входной текст, то значение признака u – это сумма всех возможных вхождений строки u в сам текст t с учетом степени разреженности u по телу t.
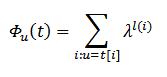
Причем за λ < 1 будет приниматься фактор, который высчитывает экспоненциальное уменьшение веса подстроки с увеличением длины подстроки в тексте.
Согласно данному определению, значения признаков здесь приравниваются к соотношению частоты встречаемости подстрок в тексте и их полной длины в тексте. Скалярное произведение текстов s и t в пространстве F здесь равно сумме значений признаков по всем строчкам с заданной длиной в n:
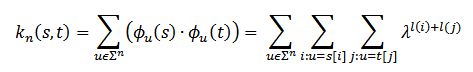
Результатом становится функция k:X→ R+, которая демонстрирует следующие свойства:
Как и следует предположить, именно эта функция представляет собой ядро SSK.
Согласно поставленным условиям и определениям, тексты, обладающие большей длиной, будут в результате давать большее скалярное произведение. Избавиться от этого эффекта можно путем нормализации ядра при помощи следующей формулы:
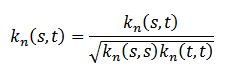
Благодаря использованию алгоритмов динамического произведения, можно вычислить это ядро неявным способом через O(|n||s||t|) операций.
В связи с высокими требованиями к производительности метода, обязательной считается работа со скоростью, выше, чем O(|n|•|s|•|t|). Для этого используется приближенное вычисление ядра.
При подсчете ядро допускает возможность «растягивания» строки по телу документа, что в свете экспоненциального уменьшения веса вхождения строки с ростом ее длины обосновывает тот факт, что многие вхождения будут обладать почти нулевым весом. Эта особенность применяется в алгоритме суффиксных деревьев (tries от retrieval trees). После ограничения максимальной длины вхождений числом m, можно применять tries, что позволяет получить линейную сложность – O(|n|•|s+t|•mm–n), однако этот подход невыгоден в нашем случае, что обуславливается необходимостью иметь n приблизительно равным 7, а m как минимум в два раза больше, последний же множитель mm–n в итоге получается чересчур большим.
Оптимальный подход, протестированный в работе, заключается в выборочном учете строк, которые включены в скалярное произведение. Этот подход основывается на постановлении:
Предположим, что S⊂X. Если |S|= dimX и вектора ф(s) признаются ортогональными при s ∈ S (k(si, sj) = Cδij для определенной константы C), то данная формула будет верна:
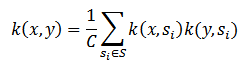
Если же вместо полного S использовать входящее в него подмножество S’, то можно говорить о приближенном равенстве:
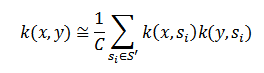
Залогом верного и эффективного приближения для функции k является подбор оптимального S’. Для выбора правильного подмножества S’ обычно используется способ пересмотра всех строчек длиной n, которые непрерывно входят во все тексты обучающего множества, и выбрать из этих строчек наиболее часто встречающиеся m (здесь число m служит для определения точности аппроксимации). Согласно данному определению ядра, все строки будут ортогональны, поэтому если рассматривать самые встречаемые строки и, чаще всего, возникающие в непрерывном состоянии, то приближение будет давать хорошие результаты. Несмотря на видимую простоту предложенного метода, исключающую использование информативных признаков, данный метод способен продемонстрировать действительно хорошие результаты даже при малом значении m.
Определение k’ дает основу для предположения, из которого следует, что нижние ряды матрицы будут практически не заполнены. Если использовать аппроксимацию, при которой общее количество строк матрицы приравнивается к длине подстроки, следующей из определения ядра, то эффект будет более ярко выражен – заполненность матрицы оценивается в порядка 10%. При этом, использование методов динамического программирования предполагает полное вычисление матрицы. Тогда оптимальным признать можно рекурсивно-динамическое программирование (рекурсия с кэшированием).
Непосредственное кэширование рекурсивного вычисления при этом будет идти на гораздо меньших скоростях, чем динамическое программирование, и это обусловлено неявным перекрытием ядер в сумме для k’:
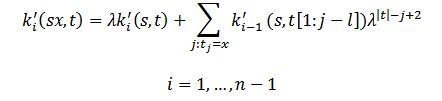
Именно поэтому внедрение дополнительной функции k’’’ (s, t, l) является обязательным, так как позволяет решить эту проблему. Дополнительная функция учитывает только те подстроки, индекс последнего символа которых завершается после параметра 1:
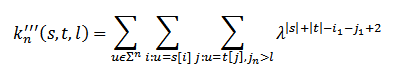
Из этого следует, что k’(s, t) = k’’’(s, t, 0), а рекурсивная запись k’’’ здесь определяется как k’ с неполной суммой:
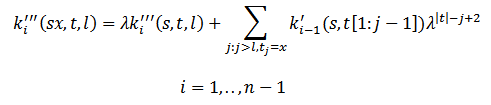
Благодаря введенным функциям, большее ядро k’ выражается через меньшее:
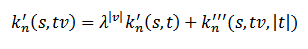
Благодаря этому введению, для выполнения задачи достаточно единичного подсчета полного ядра k’ предыдущего уровня по строке t, остальное легко вычислить инкрементально, используя k’’’. Кроме того, полное ядро k’ точно так же высчитывается через k’’’, причем использовать можно ту же формулу, где первое слагаемое – это ближайшее кэшированное k’. Сокращение скорости здесь обосновано почти десятикратным уменьшением количества умножений (следует все степени λ занести в массив). Также выиграть в скорости можно путем исключения вычисления с нулевыми (или приравненными к нулевым) весами, т.е., λx больше x. Частично изменить функцию λx также представляется возможным, поэтому можно говорить об общем повышении показателей ядра.
Для избавления от зашумленности документов при применении этого статического подхода к сравнению можно исключить применение морфологических анализаторов. Подстроки здесь используют только несколько слов, поэтому можно говорить о возможности анализа семантики сравниваемых текстов. Кроме того, добавление новых текстов здесь не влечет за собой глобальной перестройки пространства признаков с фиксированной размерностью.
Представленные алгоритмы были реализованы на Microsoft .NET 2(beta 2) посредством языка C#. Приоритетными при ведении работы были такие факторы, как открытость и расширяемость без помех задачам на продвижение сайтов. Для решения использовались библиотеки с иерархическим принципом пространства имен и открытыми интерфейсами.
Реализованная архитектура обладает несколькими преимуществами, имеющими значения в рамках выполнения поставленной задачи, а именно возможность вести параллельное вычисление в двух местах программы:
Задачу многоклассовой классификации можно решить отделением каждого класса от прочих. Это обуславливает независимости каждой бинарной задачи от других, поэтому вычисление может вестись параллельно на различных машинах. Последующая классификация предполагает определение коэффициентов принадлежности к каждому классу точно так же, на различных машинах.
Квадратичная задача оптимизации позволяет разбивать Гессиан на матрицы с большой размерностью (более 2). При этом элементы матрицы – то есть, ядра с различными коэффициентами – отличаются независимостью, поэтому при вычислении можно использовать разные машины.
Голосующий персептрон, о котором шла речь в [22], способен продемонстрировать сравнимые с SVM оценки эффективности. Тестирование может показать равную точность классификации, различается только скорость обучения и самой работы. При этом время обучения и работы персептрона можно сократить, если задействовать алгоритм уменьшения точности, и именно поэтому SVM в некотором роде можно признать более точным. Если же использовать голосующий персептрон в сочетании с ядрами SSK, то можно избавиться от проблем точности и работать в промышленных масштабах. Благодаря обобщению, голосующий персептрон также можно использовать и для решения многоклассовой классификации [22].
Основные критерии (метрики) качества, используемые при тестировании: точность, правильность, полнота и мера F1.
Точность – это характеристика, которая описывает правильность классификации текстов, сравнивая их с идеалом.
Используется отношение правильно классифицированных текстов к их общему количеству.
Прочие метрики в основном используются для оценки задачи выделения определенного класса из множества. Задачей классификатора здесь является отнесение элемента к тому или иному классу; каждый элемент проверяется на принадлежность к заданному классу, в результате чего дается положительный (positive, P) или отрицательный (negative, N) ответ. Вне зависимости от характера ответа, результат может быть и верным (True Positive, TP, True Negative, TN) и неверным (False Positive, FP, False Negative, FN). Именно через отношение количества тех и других ответов (верных и неверных) и определяется значение метрики.
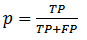
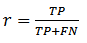
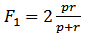
Оптимальная настройка тех или иных параметров работы классификатора обычно определяется после кросс-валидации. Если предстоит использовать множество параметров, то оценка должна вестись не для каждого из них, а для их совокупности. Настолько подробный тест, конечно, потребует задействования множества ресурсов, так как вычислительная сложность этой операции довольно высока, поэтому рассмотрим некоторые настройки параметров, которые были использованы в данной работе.
Настройки SVM:
Параметры SSK:
Выборка, которая использовалось для испытания классификаторов, включала в себя порядка 19500 страниц разных рубрик, среди которых были мобильные телефоны, психология, биология, искусство и т.п. Выборка из 19500 страниц в ходе тестирования была разделена на две равные части, первая из которых использовалась как обучающее множество, а вторая как тестовое множество. Для первичной обработки текстов использовались только простые эвристики, которые показывали те же результаты, что и сложные алгоритмы.
Использование ровно одной второй части выборки обусловлено рядом доказательств оптимальности этого решения, которые будут приведены ниже. Тестирующее множество включало в себя страниц четырех рубрик: спорт, политика, страхование, автомобили. Для демонстрации и обоснования правильности выбора была выстроена зависимость точности решения задачи разделения на два класса от размера обучающего множества.
| Размер тренировочного множества Т, % | Точность | Точность | Точность | Точность |
| — | Спорт-Политика | Спорт-Автомобили | Автомобили-Страхование | Среднее значение |
| 10 | 0.72 | 0.84 | 0.78 | 0.78 |
| 20 | 0.77 | 0.81 | 0.86 | 0.81 |
| 30 | 0.89 | 0.86 | 0.92 | 0.89 |
| 40 | 0.94 | 0.89 | 0.93 | 0.92 |
| 50 | 0.96 | 0.90 | 0.97 | 0.94 |
| 60 | 1.00 | 0.97 | 0.99 | 0.98 |
| 70 | 1.00 | 0.98 | 1.00 | 0.99 |
| 80 | 1.00 | 1.00 | 1.00 | 1.00 |
| 90 | 1.00 | 1.00 | 1.00 | 1.00 |
Таблица 1. Зависимости точности классификации при различных размерах обучающего множества.
Наглядная иллюстрация средних значений точности при разных размерах выборки можно увидеть на следующем графике:
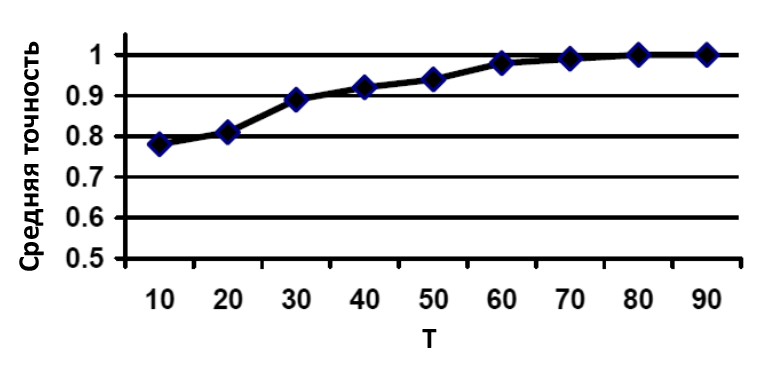
Рисунок 1 Усредненные значения точности в зависимости от размера обучающего множества.
Из приведенных выше таблицы и рисунка становится понятно, что оптимальным размером тренировочной выборки является 50%, так как при таком размере точность наиболее высока – порядка 95%. Кроме того, рисунок наглядно иллюстрирует зависимость точности результатов классификации от размера выборки (чем больше тренировочная выборка, тем точнее результаты, а исключения вроде полного отсутствия ошибок объясняются малым количеством данных).
С результатами работы различных классификаторов можно ознакомиться в следующих таблицах.
| Рубрика | Точность | Точность | Точность |
| — | p | r | F1 |
| Сотовые телефоны | 0.86 | 0.57 | 0.69 |
| Футбол | 0.89 | 0.41 | 0.56 |
| Психология | 0.90 | 0.45 | 0.60 |
| Живопись | 0.65 | 0.41 | 0.50 |
| Биология | 0.42 | 0.67 | 0.52 |
Таблица 2. Результаты решения задачи классификации персептроном.
| Рубрика | Точность | Точность | Точность |
| — | p | r | F1 |
| Сотовые телефоны | 0.89 | 0.62 | 0.73 |
| Футбол | 0.93 | 0.35 | 0.51 |
| Психология | 0.89 | 0.43 | 0.58 |
| Живопись | 0.72 | 0.38 | 0.50 |
| Биология | 0.46 | 0.72 | 0.56 |
Таблица 3. Результаты испытаний SVM.
Метод персептрона и SVM дает практически одинаковые результаты, свидетельством чего становится среднее значение F1, которое для персептрона равняется 0.57, а для SVM – 0.58. Результаты, которые не были отображены в таблицах, демонстрируют, что с увеличением данных для обработки SVM показывает лучшие результаты, но при этом улучшение результатов остается несущественным и для того, и для другого методов. Подводя итоги, можно заключить, что в целом тестирование этих методов дало положительные результаты, так как достигнуты достаточно высокие результаты – F1 в 0.60 – которые считаются приемлемыми для категоризаторов англоязычных сайтов. Оба метода способны показать достаточно большую гибкость, ведь изменяя определенные параметры можно добиваться лучших результатов как в вопросах точности результатов, так и в вопросах скорости работы за счет использования кластерного масштабирования. Данная работа своей целью имеет привлечь внимание к дальнейшей работе над испытанными алгоритмами с целью их оптимизации и возможности применения в дальнейшем на практике.
Рерайт материала «Классификация Веб-страниц на основе Алгоритмов Машинного Обучения» выполнила Инна Вдовицына
Полезная информация по продвижению сайтов:
Перейти ко всей информации