SEO-Константа
Яндекс.Директ + оптимизация
В данной работе анализируются методы машинного обучения ранжирования, основанные на списочном подходе (Listwise Approach), в частности на перестановке документов. Минимизация функции потерь в связи с использованием подобным методов. Что такое свойство состоятельности и определение формулировки критерия состоятельности; исправления и дополнения к первоначальной формулировку критерия.
Одной из главных задач при разработке алгоритмов поиска текстовых документов по запросу является их ранжирование в соответствии со степенью релевантности самому запросу – наиболее релевантные документы должны выводиться в списках в первую очередь и далее по уменьшению степени релевантности. Сама по себе задача ранжирования текстовых документов по релевантности делится на две подзадачи – это выявление признаков релевантности (т.е. факторов ранжирования) и построение функции ранжирования, основанных на этих факторов и весовых коэффициентов, которые задаются машинным обучением.
Признаки релевантности – это совокупность самых различных показателей. В качестве факторов ранжирования, присвоенных паре запрос-документ, может быть использована и частотность запроса в теле документа, и его длина, и более сложные характеристики документа и запроса. Такие поисковики, как Google и Яндекс, используют в своей работе до нескольких сот подобных факторов и признаков релевантности. Сама функция ранжирования, которая позволяет ранжировать документы по их релевантности запросу, выстраивается на основе базы данных, в которую входит несколько тысяч примеров оценки пар «запрос-документ» асессорами, причем оценка выставляется с учетом нескольких градаций релевантности. Функция выстраивается путем линейной комбинации факторов с весами, которые выбираются при помощи одного из алгоритмов машинного обучения задачам ранжирования. Сегодня используется сразу несколько типов методов машинного обучения задачам ранжирования текстовых документов, причем большая их часть эвристического характера – методы на практике показывают отличные результаты, но при этом не имеют строгого теоретического обоснования. Кроме того, на данный момент существует одна значительная проблема, а именно проблема объективного сравнивания принципиально разных методов, что связано с отсутствием теоретического анализа алгоритмов. На данный момент в основном используется эмпирический способ сравнения, основанный на сопоставлении результатов различных алгоритмов, именно поэтому в рамках конференции ACM SIGIR LR4IR 2007 группой Tie-Yan-Liu был предложен способ унифицировать результаты тестированием путем использования коллекции LETOR.
Первые статьи, затрагивающие проблему глубокого анализа алгоритмов обучения, вышли в 2008 году. Работа проводилась на основе подхода, описанного в статье [2], которая была опубликована в рамках конференции ICML. Исследователями был предложен единый критерий состоятельности, создающий необходимые условия на функцию штрафа, в результате чего функция становится эффективной в свете задачи машинного обучения задачам ранжирования. [Если говорить о практическом применении алгоритмов машинного обучения в поисковых системах, то на сегодня известно, что Яндекс использует для данных целей MatrixNet, а Bing — RankNet. Мы полагаем, что текущий материал будет очень полезен для всех, кого интересует продвижение сайтов в системах информационного поиска, доверяющих ранжирование сайтов алгоритмам машинного обучения — прим. коллектива компании «SEO константа»]. В ходе работ, автор установил, что ранее принятый критерий состоятельности выдает не совсем корректные результаты, если параллельно с ним не создается дополнительных условий на функции штрафа. Именно поэтому следующим шагом работы стала проработка контрпримера к оригинальной теореме, результатом чего стала разработка нового критерия состоятельности и доказательство теоремы.
Теорема о состоятельности дала возможность разработать и проанализировать новый алгоритм, который по своим результатам в области ранжирования документов по релевантности запросу превзошел предыдущий метод. Этот метод прошел тестирование на одной из наиболее часто используемых тестовых коллекций, а результаты испытания оказались сравнимы с результатами одного из лучших ранее опубликованных алгоритмов.
В поставленной и сформулированной задаче ранжирования приняты были следующие условия:
Согласно условиям, задача требует наличия еще одного множества – множества R, на котором задан линейный порядок ≺. Таким образом, функция ранга ψ:(Θ × D → R) необходима для определения релевантности текстового документа поисковому запросу. Из этого следует, что два однотипных документа d1 и d2 будут характеризоваться разной релевантностью запросу q; например, если ψ(q,d1)≺ψ(q,d2), то d1 менее релевантен запросу q, чем d2. Также допускается введение упрощающего обозначения ψq = ψ(q,⋅). Перестановки типа представляют собой сортировку документов по убыванию ранга. Эту перестановку можно связать с любой из пар типа ψqi, {dij}j. Кроме того, допускается введение дополнительного обозначения типа sort (а⃗) = π, которое упрощает обозначение перестановки сортированного списка значений ai:aπi > aπj, когда i<j. Следовательно, πqi = sort({ψqi(dij)}j).
Также потребуется введение множества признаков, которое будет обозначено множеством функций F, его же элементы – признаки релевантности и суть функции φ:ΘxD → ℜ. Именно благодаря введению этого множества, а также использованию таких элементов, как признаки, становится возможным численно связать документ и сам запрос. Следующим этапом работы будет постановка самой задачи обучения ранжированию. Здесь в качестве базы знаний использоваться будет так называемое обучающее множество, то есть, объединение множества запросов и множества документов с определенной функцией ранга, следовательно, обучающее множество выражается таким образом:
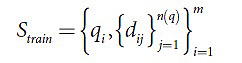
Где qi∈Θ, dij∈D и для каждой пары qi и dij установлено значение ψ(qi,dij).
Тестовые и обучающие множества совпадают за тем лишь исключением, что обучающие запросы и соответствующие им документы различаются. В задаче тестовое множество будет выражено обозначением типа Stest. Основной проблемой обучения ранжированию документов является нахождение наиболее оптимальной эмпирической функции ранжирования типа ψ~:ℜr → ℜ при ее использование в заданном обучающем множестве, причем r является мощностью пространства F. Оптимальность ψ~ на практике определяется условием ψ~= argmax E (ψ~,ψ, Stest). При этом функционал Е позволяет измерить близость функции ранга и эмпирической функции ранжирования. Функция, сопоставляющая перестановку документов по убыванию значений ψ~ с запросом q, в нашей задаче будет обозначена за πψ~(q). Отсюда: ψ~(q,di)>(q,dj)⇔πψ~(q)(di)<πψ~(q)(dj)
На сегодняшний день в теоретическом анализе ранжирования текстовых документов чаще всего используются метрики NDCG (Normalized Discounted Cumulative Gain) и MAP (Mean Average Precision). В записях часто встречаются обозначения типа NDCG@N, но это применимо только в ситуациях, когда суммирование ведется только по N самых релевантных документов.
В качестве ограничения эмпирической функции ранжирования мы будем предполагать её линейной. В векторной форме ψ~(x⃗ )=<ω⃗,x⃗>, при этом ограничение не концептуально. Для иллюстрации утверждения можно привести пример, где в роли функции ранжирования выступает нелинейная нейронная сеть, которая определяется определенной группой операций (генетическое программирование). Перечисленные методы позволили добиться достаточно высоких результатов с нелинейными функциями ранжирования, таким образом, доказав, что использовать можно не только линейные функции. Эти исследования открыли в качестве одной из перспектив для дальнейших исследований выбор гораздо более сложных моделей функций ранжирования и алгоритмов ее обучения задачам ранжирования. Если сравнивать линейные и нелинейные функции ранжирования, то первая способна продемонстрировать следующие преимущества:
В этом разделе мы рассмотрим некоторые алгоритмы машинного обучения, которые в качестве объектов обучения используют перестановки документов. Множество П включает в себя множество перестановок, поэтому отображение ранжирующих функций здесь будет h:Θ → П. Тогда результирующая перестановка здесь назначает порядок документов в соответствии с убывающим рангом документов типа dij (при этом размерность перестановки приравнивается к n(qi)). В данном случае функцию ранга может заменить вероятностное распределение на множестве Θ×П, определяющее релевантность перестановки запросу. Распределение можно принять за P, поэтому допустимо ввести функцию ожидаемых потерь, выражающую среднюю по вероятностному множеству (1):
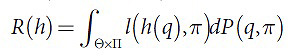
Использованная здесь функция риска l(π1,π2) является 0-1 функцией потерь. Иными словами, l(π1,π2)=1 в том случае, если π1≠π2 или иное при l(π1,π2)=0. При этом минимум функции R(h) достигается на h(q)=argmax p(q,π). Применяемая для обучения эмпирическая функция ожидаемых потерь в данном случае записывается в следующей форме (2):
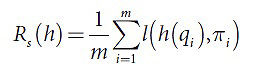
Применение общепринятых методов оптимизации здесь осложняется разрывностью данной эмпирической функции, и именно поэтому вместо функции l лучше использовать другие функции, которые гораздо лучше подходят для оптимизации. Например, функция ожидаемых потерь заменяется суррогатной функцией потерь Φ, которая записывается следующим образом (3):
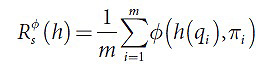
Согласно поставленным условиям, крайне важно, чтобы следствием минимизации функции Rφs(h) была минимизация R(h), откуда следует нахождение h(q)=argmax p(q,π). Данное свойство функции Φ в нашей работе получает название состоятельности, однако далее нам потребуется некоторая формализация.
Примем пространство ΛП за множество возможных вероятностных распределений на множестве, состоящее из перестановок П (4):
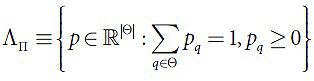
Если выполняются такие условия, как:
Тогда подмножество Ω⊂ℜn считается рабочим подмножеством. Критерий состоятельности присваивается функции φ на рабочем подмножестве Ω относительно функции ожидаемых потерь R, если выполняются следующие условия: если обозначим за π*=argmax (pπ), а за πсπ*= π{π*}, тогда (5):
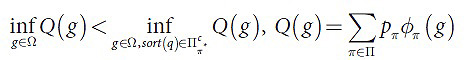
Проверка такого свойства, как состоятельность, может быть довольно трудной, поэтому в статье [2] вы сможете найти подробное расписание условий, достаточных для признания функции состоятельной. В статье не было приведено полное доказательство теоремы в виду нехватки места, однако при этом основ достаточно для пояснения критерия самостоятельности. Автором настоящей работы было доказано, что приведенная в статье [2] формулировка самой теоремы не совсем верна, с чем согласились авторы самой статьи, поэтому здесь будет рассматриваться несколько иная формулировка, в которую будут включены дополнительные условия, а также приведено полное доказательство теоремы. Для составления корректной формулировки теоремы требуется ввести несколько дополнительных определений, в которых под φπ будет подразумеваться, как и прежде, φ(π,⋅). Определения:
I. Пространство Λπ сохраняет порядок объектов (a,b), когда для любой пары перестановок π и σ, отличающихся всего лишь позициями a и b (a в π стоит выше, нежели чем b), выполняется pπ>pσ.
II. Класс функций φπ чувствителен к порядку при соблюдении:
В этом разделе будет приведен первоначальный вариант формулировки критерия состоятельности, который был описан в статье [2]. Согласно первоначальной формулировке, пусть функция φ является чувствительной к порядку на подмножестве Ω. При этом вероятностное пространство перестановок для некоторых n-объектов должно сохранять порядок объектов (a1, a2), (a2, a3),…, (an-1, an). При соблюдении вышеперечисленных условий φ признается состоятельной в отношении функции R на рабочем подмножестве Ω. Проведенные в этой работе исследования доказывают, что данная формулировка критерия состоятельности неверна.
Для начала следует изучить функцию потерь типа φ1,2=1/1+eg1-g2, φ1,2=0.5/1+eg1-g2 +0.25. В ходе дальнейшего анализа было установлено, что φπ(g) должна быть чувствительна к порядку на ℜ2. Условием задачи установлено, что вероятностное пространство перестановок Λ включает в себя два элемента (аналогичных перестановкам (1,2) и (2,1) соответственно) – это p1,2=0, p2,1=0. Согласно данному ранее определению, пространство Λ должно соблюдать строгий порядок в отношении второй пары (2,1), что дает основания заключить, что условия первого утверждения полностью соблюдены. Также примем Ω={x,y:max(|x|,|y|)≤100}, следовательно, функция φ не может считаться состоятельной на Ω⊂ℜ2:Q(g)=φ2,1(g) и левая часть неравенства 5: inf Q(g)= infφ2,1(g)=φ2,1(100,-100), а его правая часть: infsort(g)=1,2Q(g)= infd>0(φ2,1(g))=φ2,1(100,-100), где d=g1-g2. Из этого следует, что первое утверждение неверно. На Рисунке 1 наглядно показано, что предполагаемая функция имеет чувствительность к порядку.
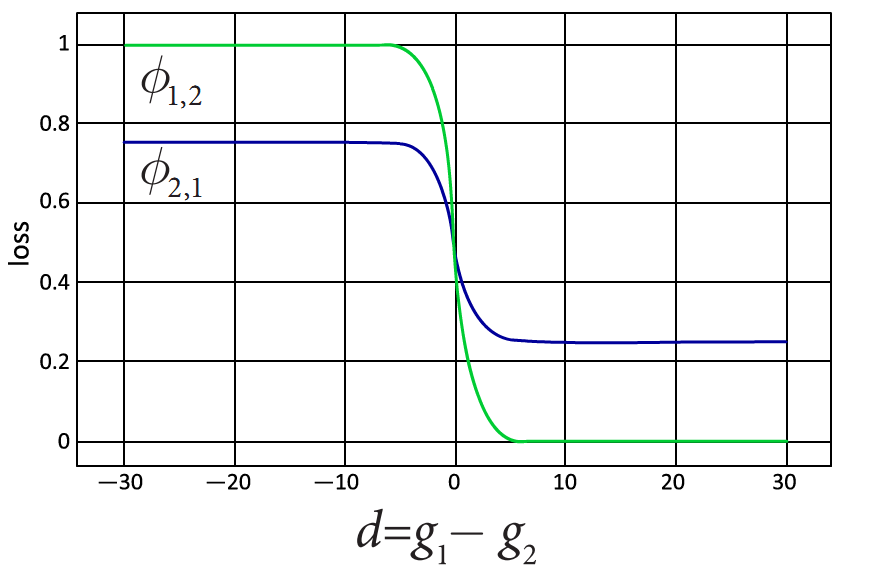
Рисунок 1. График функции.
Для начала скажем, что функция φπ(g)не отрицательная, дифференцируемая на R2. Рисунок, отображающий график функции, демонстрирует нам, что φ1,2<φ2,1 если d>0. Аналогично φ1,2>φ2,1 если d<0. Отсюда вытекает условие (3) из определения чувствительности нашей функции к порядку. Свойство (4) следует из того обстоятельства, что g1=g2 исключительно для d=0, однако при этом: (φ1,2)’g1 (d=0)≠(φ2,1)’g2(0) поскольку (φπ)’g1|d=0 и (φπ)’g2|d=0 имеют разные знаки. Из этого следует, что функция φ чувствительна по отношению к порядку.
Исправление первой, неверной формулировки признака состоятельности потребует от нас введения дополнительного определения. Функцию φ можно признать симметричной, если φπ(g)=φσπ(σg), где σ∈П, причем произведение перестановок трактуются в естественном смысле, а σg=h, такое что gi=hσ(i)*. Исправленная формулировка критерия состоятельности в этом случае должна быть следующей.
Теорема. Если симметричная функция φ на рабочем подмножестве Ω чувствительна к порядку, и для некоторых n-объектов вероятностное пространство перестановок будет сохранять порядок объектов (a1, a2),(a2,a3),…,(an-1,an), тогда φ может признаваться состоятельном в отношении функции R на рабочем подмножестве Ω. Её доказательством служит тот факт, что ai=i, тогда π*=(1,2…n)=Id. Тогда можно обозначить Ω’={g∈Ω:gi≠gj,i≠j}.
Лемма. Для любой g∈Ω’, sort(g)≠π* в Ω’ найдется вектор g’:sort(g’)=π*, при котором Q(g’)<Q(g). Доказательство леммы: существование двух индексов i<j, при которых g(i)<g(j), следует из того, что sort(g)≠π*. В этом случае инверсию элементов i и j обозначим за σ, тогда пускай g’=σg. Дальнейшее доказательство требует расписать Q(g)–Q(g’) по определению:
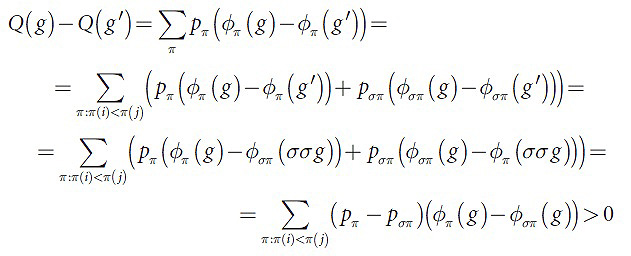
Так как σσ=Id и по определению функции, которая чувствительна к порядку по свойству 3 φπ(g)≥φσπ(g), и минимум для одного π строгое неравенство верно, тогда:
Лемма. Верным является следующее равенство:
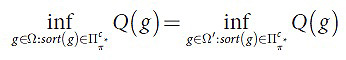
Так как множество Ω компактно, то множество Ωc={g|∈Ω:sort(g)∈Пcπ*} также считается компактом. Из этого следует, что минимум на Ωс должен достигаться на векторе этого подмножества, поэтому будем считать, что минимум Q(g) достигается на векторе g и ∃i,j:i≠j, при которых gi≠gj. Из этого следует, что по свойству (4) чувствительности φ получаем, что (9):
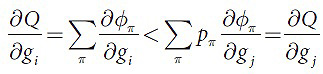
в противном случае, неравенство будет соблюдаться в обратную сторону. Данное неравенство будет строгим, так как из свойства 2 следует, что минимум для одного π неравенство является строгим. Отсюда, условия ∂Q/∂gi|g=0 и ∂Q/∂gj|g=0 не совместны, поэтому точка g не может быть стационарной. Поэтому, не верно, что ∃i,j:i≠j, при которых gi≠gj. Тогда, g∈Ω’.
Продолжение доказательства теоремы. Вторая часть доказательства заключается в использовании леммы 9, которая предполагает доказательство (10):
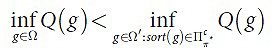
Согласно определению леммы 8, для любого элемента g∈Ω’:sort(g)∈Пcπ* должен существовать элемент g’∈Ω, при котором Q(g)>Q(g’). Поэтому, пользуясь компактностью Ω, нам удается получить необходимое неравенство.
Принятый за истинный доказанный критерий состоятельности может использоваться для доказательства состоятельности самой функции, применяемой алгоритмами ранжирования.
Примем за wi неотрицательную монотонную возрастающую последовательность (16):
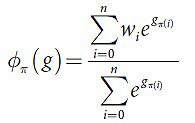
В данном случае доказательство критерия состоятельности заданной функции основывается на доказательстве такого свойства, как чувствительность к порядку. В первую очередь необходимо доказать, что все условия определения соблюдены:
Укажем выражение для частной производной φπ, где π=Id (17):
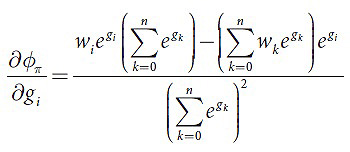
Принимая во внимание это выражение, при условии, что gi=g, i<j, получим следующее (18-19):
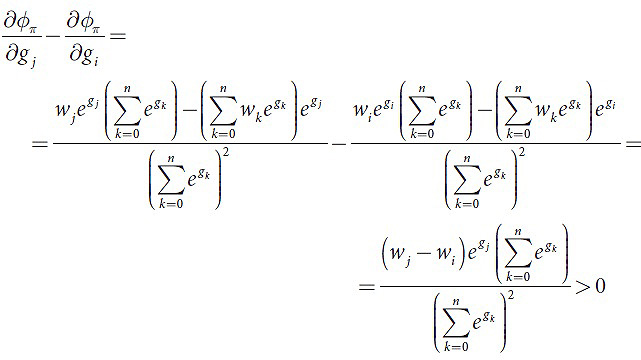
что доказывает чувствительность функции φ к порядку.
Метод минимизации функции потерь заключается в использовании определенной суррогатной функции, которой свойственен весь необходимый для решения задачи минимизации набор свойств. Минимизируемая функция, кроме того, должна коррелировать с метриками, согласно которым ведется оценка качества сортировки веб-документов в поиске. Первые наброски этой идеи можно найти в одной из наиболее ранних публикаций, например, в статье [2] затрагивается возможность использования функцию потерь, основанной на правдоподобии. В этой же работе вы сможете найти не только описание исправленного подхода к минимизации функции потерь, ряд доказательств утверждений, но также и попытку воспроизведения результатов, опубликованных в [2]. Метод, использующий в своей основе функцию правдоподобия (MLE — Maximum Likelihood Estimation), был не единственным алгоритмом, который был задействован в настоящей работе. Наша модификация, основанная на обобщении функции потерь, показала значительно лучшие результаты, нежели чем функция правдоподобия.
Давайте рассмотрим нашу модификацию более детально. Этот алгоритм рассматривает только класс линейных ранжирующих функций, каждая из которых может быть задана вектором весов ω. Он также включает в себя этап обучения и ранжирования. На этапе обучения основной поставленной задачей является поиск оптимального набора весов ω для нашего обучающего множества. На этапе ранжирования найденный набор весов скалярно умножается на множество входных значений, релевантных определенным значениям характеристик выбранной страницы.
Предложенный нами обучающий алгоритм на вход получает набор из m-списков значения признаков (данные отранжированы в порядке убывающего соответствия), каждый из которых соответствует полученным результатам использования функции Φqi на парах (qi, dij). В каждом использованном наборе значений признаков, соответствующего определенной интернет-странице, указана степень ее релевантности к пользовательскому запросу. Основной проблемой тестирования здесь является плохое градирование степени релевантности, поэтому для получения отранжированного списка нам необходимо определиться с упорядочиванием страниц внутри коллекции со схожими оценками релевантности. Для решения этой проблемы было предложено два принципиально отличных подхода:
Примем, что n(qi)=n,∀qi, а за r примем размеренность пространства признаков.
Алгоритм предполагает использование следующих функций (24-25):
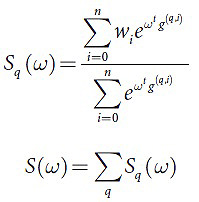
Для вычисления функции штрафа необходимо выполнить O(mnr) операций. Минимизация в данном случае предполагает применение градиентного спуска c адаптивным выбором шага. В качестве монотонно возрастающей функции wi тестируются разные последовательности, среди которых лучшие результаты продемонстрировали: wi=log(i+1), i∈[1,n]; wi=log2(i+1), i∈[1,n]. Согласно данному ранее определению выбранная функция S является состоятельной. Выполнение заданных алгоритмом задач останавливается по мере изменения значения функции штрафа ниже заданного порога ε. На выходе мы получаем набор весов ω=(ωi)1r, где достигается минимальное значение функции штрафа.
Здесь в качестве входных значений используется тот же набор весов ω=(ωi)1r, а также множество страниц, заданные значениями своих характеристик. Для каждого картежа значений признаков алгоритм ранжирования возвращает значение ранга (в точном соответствии с документом), при этом ранг высчитывается по формуле ωtg(q,i), причем за g(q,i) принимается кортеж значений характеристик.
Предложенные алгоритмы были испытаны на тестовой коллекции OHSUMED 3.0, которая является одной из составляющих коллекций LETOR 3.0. Наша коллекция OHSUMED 3.0 включала в себя порядка 45 признаков с нормализацией их значений по запросам.
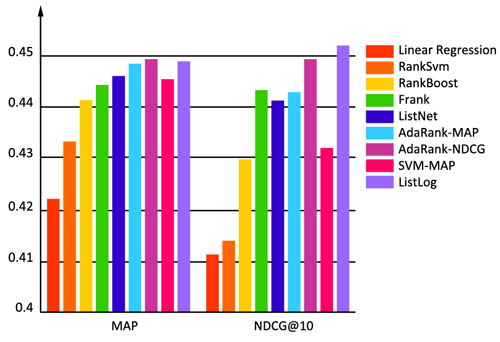
Рисунок 2. Сравнение результатов работы алгоритма ListLOG с весами log2 с результатами ранее опубликованных методов.
Использование этой тестовой коллекции оправдано в силу того, что результаты тестирования других алгоритмов в этой коллекции опубликованы, поэтому можно объективно сравнивать результаты разных алгоритмов. На графике (рис.2) наглядно отображены результаты опубликованных ранее алгоритмов и предложенного в данной работе ListLOG. Для сравнения предложены результатов по двум метрикам оценки качества ранжирования – MAP и NDCG@10, причем в первом случае ListLog по результатам уступает AdaRank-NDCG, однако во втором случае предложенный алгоритм показывает лучшие результаты.
Использованы следующие методы, чьи результаты отображены на графике:
Алексей Тимофеев, МГУ им. М.В. Ломоносова, Москва
Рерайт материала выполнила Инна Вдовицына
Полезная информация по продвижению сайтов:
Перейти ко всей информации