SEO-Константа
Яндекс.Директ + оптимизация
Техника гиперссылочного спама используется веб-мастерами и поисковыми оптимизаторами в целях увеличения рейтинга определенных целевых страниц посредством введения в заблуждения алгоритмов ссылочного ранжирования систем информационного поиска. В данной работе мы изучаем то, каким именно образом интернет-страницы могут быть комплексированы в так называемую спам-ферму для оптимизации своего рейтинга. Мы также исследуем манипулятивные альянсы, то есть комплексирование множества спам-ферм. Результаты нашей работы позволяют идентифицировать оптимальные структуры и дать количественную оценку потенциальным выгодам. В частности, мы демонстрируем, что подобного рода альянсы могут иметь синергетический эффект и улучшать показатели ранжирования всех их участников. Мы полагаем, что более глубокое понимание сути проблемы поможет нам идентифицировать ссылочный спам, а также оказывать ему эффективное противодействие.
Поскольку на сегодняшний день системы информационного поиска стали повсеместно используемым инструментом нашей повседневной жизни, не только бизнес-структуры, но и частные лица часто желают видеть принадлежащие им веб-странички на лидирующих позициях результатов органической выдачи, возвращаемых поисковыми машинами в ответ на пользовательские запросы. Экономическое преимущество, получаемое в случае нахождения интернет-ресурса на первой странице поиска привело к возникновению темного искусства спамденсинга [3]: ряд вебмастеров и поисковых оптимизаторов создают такой веб-контент, единственная цель которого заключается в ведении в заблуждение поисковых систем и получения незаслуженно высокого рейтинга в результатах органического поиска. Успешные попытки подобного рода манипуляций вызывают возмущения в возвращаемых машиной результатах, а также приводят к ухудшению качества поиска, поскольку те интернет-страницы, которые обладают истинной популярностью, подменяются неестественно раскрученными низкокачественными документами. Уравновешивание того негативного эффекта, который вызывается все возрастающим объемом поискового спама, представляется серьезной проблемой для современных систем информационного поиска [4]. Среди всего изобилия манипулятивных практик, используемых спамерами, существует такая, которая заслуживает особо пристального внимания — это ссылочный спам. Гиперссылочный спам относится к тем случаям, когда спамерами создаются структуры взаимосвязанных страниц, называемых ссылочными спам-фермами, и единственная задача которых сводится к увеличению показателей, присваиваемых алгоритмами ссылочного ранжирования, чаще всего PageRank [7], одной или небольшого числа целевых страниц. Решение проблемы ссылочного спама важно не только по той причине, что он может достигать значительных успехов в улучшении видимости целевых страниц, но также и потому, что многие случаи его проявления крайне сложно поддаются какой-либо детекции. В текущей работе мы занимаемся анализом того, каким образом ссылочные спамеры манипулируют оценками, присваиваемые алгоритмом ранжирования Google PageRank. Изучение проблемы разделено на два этапа. Сначала мы анализируем способы, с помощью которых оптимизаторы и вебмастера могут улучшить видимость только единственной целевой страницы. Затем мы исследуем тот вариант, при котором группы спамеров могут сотрудничать, формируя альянсы взаимосвязанных спам-ферм. В последнем сценарии мы полагаем, что отдельные спамеры уже обзавелись собственными спам-фермами. Они также желали бы кооперироваться с другими владельцами ссылочных ферм либо на основании взаимовыгодного участия, либо на основании финансового соглашения между участниками. Как мы увидим с вами впоследствии, посредством тщательно продуманного взаимодействия спам-ферм, подобного рода кооперация может быть взаимовыгодной для всех участников манипулятивной схемы. Несмотря на то, что относительно недавние исследования математических свойств PageRank [1, 6] затрагивали тему ссылочного спамденсинга, наша работа представляет собой более детальное обсуждение, посвященное озвученной проблеме. Важно отметить, что вопреки тому обстоятельству, что нашей конечной целью является противодействие ссылочному спаму, в текущей работе мы всего лишь сосредотачиваемся на изучении различных манипулятивных структур, а также спамерских альянсов, которые могут оказывать воздействие на результаты органического поиска. Мы кратко затрагиваем тему противодействия гиперссылочному спаму в Разделе 7, в котором мы поясняем то, каким образом наше понимание манипулятивных структур может оказать полезным в обнаружении данных схем. Касательно текущей работы у некоторых ее читателей может возникнуть вполне очевидный вопрос, который заключается в том, не поспособствуем ли мы мошенникам в реализации их обманных практик, предоставляя результаты наших исследований? Спешим ответить, что наш опыт показывает, что все представленные здесь манипулятивные техники уже сейчас широко используются в крупном сообществе спамеров. Вклад этой работы заключается в том, что мы просто формализуем данные ссылочные структуры, проводим их количественную оценку их воздействия на механизмы ранжирования, а также сравниваем их друг с другом.
Оставшаяся часть данной работы организована следующим образом. Сперва мы предлагаем обзор алгоритма Google PageRank, широко используемые алгоритм ранжирования, который мы исследуем с позиции ссылочного спама. Затем, мы обсуждаем нашу модель в контексте реализации спам-фермы; опираясь на свойства алгоритма PageRank, мы выводим ее оптимальную внутреннюю структуру. Разделы 4 и 5 сперва фокусируются на оптимальной структуре двух взаимосвязанных спам-ферм; далее мы также анализируем крупные альянсы ссылочных ферм. Затем, мы обсуждаем, как мы можем применить полученные результаты к характерным ссылочным структурам.
В текущей работе мы используем общепринятую графовую модель для представления веба — системы взаимосвязанных гипертекстовых документов. Пусть G=(V,E) является веб-графом с вершинами V, представляющих интернет-страницы, и ориентированными невзвешенными ребрами E, представляющих гиперссылки между страницами. Просим учесть, что мы исключаем наличие на нашем веб-графе петель — ссылок, инцидентных одной и той же странице. Как вы увидите, страницы без исходящих гиперссылок играют важнейшую роль в нашем анализе. Такие цифровые документы обычно называют стоковыми (sink pages). В общем виде нашему графу соответствует матрица переходов T = (Ti,j)n×n, определяемая как

,где out(i) является полустепенью исхода страницы i, то есть количество ссылок (ребер) исходящих с документа i.
Для того, чтобы упорядочить результаты органической выдачи, возвращаемых в ответ на пользовательские запросы, системы информационного поиска обычно комбинируют ряд ранжирующих механизмов. Одним из наиболее известных алгоритмов ранжирования является PageRank [7], который рассчитывает глобальные оценки авторитетности по всем интернет-страницам. Поскольку присваиваемые им оценки определяются гиперссылочной структурой веба, PageRank представляется естественной мишенью ссылочных спамеров. В нашей дискуссии мы сфокусируемся на структурах гиперссылочного спама, ориентированных на алгоритм PageRank. Затем, мы предлагаем краткий обзор Google PageRank. Давайте введем константу c, называемую коэффициентом затухания (damping factor). Оценки PageRank будет соответствовать стационарному распределению цепи Маркова [5], в которой:
Традиционная формулировка проблемы PageRank основана на системе собственных векторов, соответствующих Марковской матрице. Для целей настоящей работы мы определяем вектор оценки PageRank p как решение матричного уравнения:
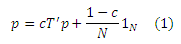
где c является коэффициентом затухания, T’ — транспортированной матрицей переходных вероятностей, N — общим числом интернет-страниц, а 1N представляет собой вектор, состоящий из N элементов в сумме равных 1. Следовательно, наша формулировка основана на линейной системе, которая не только дает схожие относительные оценки интернет-страниц как в случае использования традиционной формулировки, но и кроме этого обладает рядом дополнительных преимуществ [6].
В первой части нашей работы мы вводим модель спам-фермы, а также исследуем то, какая гиперссылочная спам-структура позволяет получить наиболее высокую голосующую способность целевого документа. Это послужит основой для анализа манипулятивных альянсов (Раздел 4) и прочих гиперссылочных спам-структур, которые в некотором роде отличаются от представленных ранее (Раздел 6).
Как упоминалось в Разделе 1, ссылочный спам ориентируется на манипуляцию алгоритмами ранжирования, которые назначают авторитетность тем или иным документам исходя из гиперссылочной структуры веба. В целях увеличения рейтинга некоторых своих интернет-страниц, спамеры часто создают (большие) группы веб-документов с тщательно продуманной структурой внутренних взаимосвязей. Мы будем называть данную группу страниц, подконтрольных спамеру, ссылочной спам-фермой (link spam farm) или, просто, спам-фермой. Исходная модель гиперссылочной спам-фермы, которую мы используем в настоящей работе, основывается на следующих правилах:
Просим обратить ваше внимание на то, что спамер не располагает полным контролем за страницами, гиперссылочная структура которых подвержена хиджакингу, то есть он не способен ни оказывать существенного воздействия на присваиваемые им оценки алгоритмом PageRank, ни определять где и каким образом будут распределены оценки по исходящим с них гиперссылкам. Следовательно, фактический объем лекажа достаточно независим от предпринятых усилий веб-спамера — используя технологию хиджакинга, спамер может только ограничиться получением максимально возможного числа входящих ссылок, отдавая предпочтение тем интернет-страницам, которые подозреваются в наличии высокого PageRank.
Давайте рассмотрим спам-ферму, состоящую из k-стимулирующих страниц плюс одного целевого документа. Возможно идентифицировать целый класс манипулятивных структур, который позволяют получить целевому документу высокую оценку PageRank. на Рисунке 1 представлена одна из подобного рода оптимальных структур.
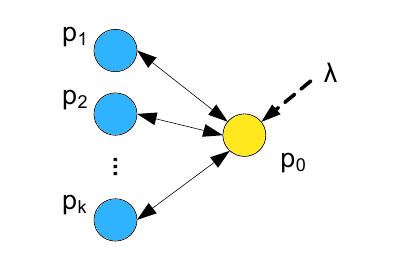
Рисунок 1. Оптимальная структура единичной спам-фермы с одной целевой страницы
Глядя на Рисунок 1, можно увидеть, что k-стимулирующих страниц и целевой документ взаимно ссылаются друг на друга, а все внешние входящие гиперссылки, реализованные с помощью практики хиджакинга, цитируют целевой документ, обеспечивая лекаж λ. Для начала давайте взглянем на оценку целевой страницы, которая достигается посредством использования данной структуры. Затем, мы докажем наличие возможности достижения более высокой оценки целевого документа.
Теорема 1. Оценка PageRank p0 целевой страницы, представленной на Рисунке 1, рассчитывается как:
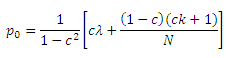
Доказательство. В соответствии с Уравнением 1, оценки, получаемые спам-страницами из Рисунка 1, определяются по следующей системе:

Заменяя pi в первом уравнении, получаем:
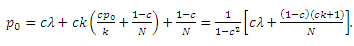
В данном подразделе мы идентифицируем класс манипулятивных структур, с помощью которых целевая страница может достичь наиболее высокой голосующей способности. Рассмотрим характерную для этого класса спам-ферму, отображенную на Рисунке 2, с единственной целевой и k-стимулирующих страниц.
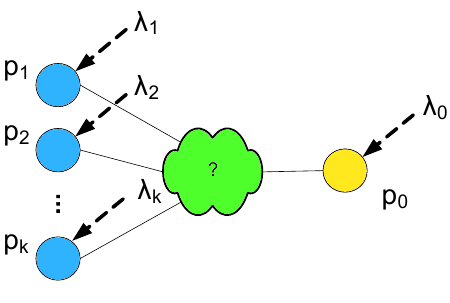
Рисунок 2. Типичная манипулятивная структура, использованная в Теореме 2.
Документы спам-фермы связанны между собой произвольным образом. Спам-страницы могут иметь исходящие гиперссылки на сторонние веб-узлы, которые не входят в состав линкофарма (хотя на Рисунке 2 подобные линки опущены). Гиперссылки, созданные с использование практики хиджакинга, ссылаются на веб-страницы, состоящие в линкоферме таким образом, чтобы лекаж цели составлял λ0 ≥ 0, а стимулирующей страницы i λi ≥ 0. Тогда, общий лекаж λ = λ0 + · · · + λk. Просим обратить ваше внимание на то, что вопреки тому, что спам-страницы могут цитировать качественные документы и, следовательно, оказывать некоторое влияние на лекаж, на основании Предположения 3 из подраздела 3.1, λi фактически не зависит от голосующей способности спам-страниц. Мы вводим в нашу модель две вектора p и λ для PageRank и лекажа стимулирующих страниц,
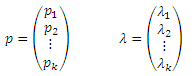
Учитывая это, матричное уравнение оценок PageRank документов спам-фермы можно переписать следующим образом:
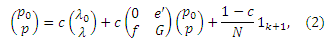
где вектор-строка e’ соответствует весам ссылок, исходящих со стимулирующих страниц к целевой, f содержит веса ссылок, исходящих с целевой страницы к стимулирующим, а G – матрица весов, охватывающая взаимосвязи между стимулирующими страницами.
Теорема 2. Оценка PageRank целевой страницы p0 является максимальной в том случае, если спам-ферма представляет собой такую структуру, что e=1k, 1’kf=1, G=0kxk, а λ0 = λ и λi = 0, для i=1,…,k.
Доказательство. Представленное далее доказательство продолжает (обобщает) то, что было представлено первоначально в [1] также разрешая лекаж. Давайте сначала перепишем Уравнение 2 в систему
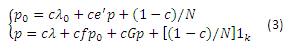
и умножим обе части второго уравнения на 1’k:
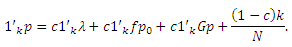
Введем скаляры α, β, и γ:
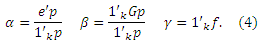
Они обладают следующими свойствами: α, β, γ ≥ 0; α + β ≤ 1; и γ ≤ 1. Просим обратить ваше внимание на то, что α + β=0 только в том случае, когда все стимулирующие страницы являются стоковыми; находятся в строго определенном диапазоне от 0 до 1 тогда, когда некоторые стимулирующие страницы являются стоковыми и/или цитируют документы, находящиеся за пределами спам-фермы; и только тогда составляют 1, когда все стимулирующие страницы ссылаются на цель и только на неё. Аналогично, γ меньше, чем 1 в том случае, если целевая страница является стоковой или имеет исходящие гиперссылки за пределы линкофермы; и составляет 1 в том случае, если целевой документ указывает на некоторые или на все стимулирующие страницы. Также, легко заметить, что
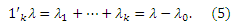
Используя Уравнения 3, 4 и 5, мы получаем следующую систему:
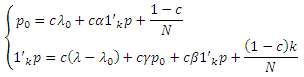
Соответственно,
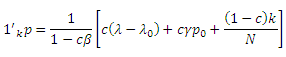
и
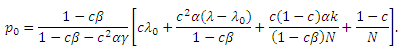
По причине свойств α, β, и γ, 1 − cβ − c2αγ > 0. Кроме того, p0 монотонно убывает в γ. Следовательно, вне зависимости от прочих факторов, γ должен соответствовать 1 для того, чтобы достичь максимального p0. Заменяя γ на 1, PageRank целевой страницы становится:
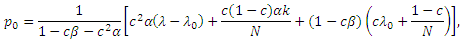
где p0 является функцией α, β и λ0. Также, необходимо напомнить, что лекаж λ0 не зависит от внутренней структуры спам-фермы или оценок PageRank спам-страниц. Соответственно, частной производной p0 относительно β является
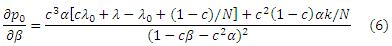
которая всегда неотрицательная для β ∈ [0, 1], равная нулю в том случае, если α=0. Следовательно, p0 максимальна на границе α + β = 1. Заменяя β = (1−α) в Уравнении 6, давайте вычислим частную производную p0 относительно α:
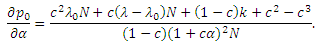
Как числитель, так и знаменатель производной положительны, следовательно p0 монотонно возрастает в α и достигает своего максимума в α=1. Заменяя α=1, уравнение p0 принимает вид
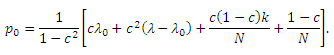
Частная производная относительно λ0 положительна:
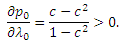
Следовательно, p0 достигает своего максимума при достижении λ0 своего наибольшего значения λ0= λ. В этом случае, λ1 = λ2 = … = λk = 0. Соответствующее максимуму p0 является уравнение:
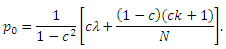
Подводя итог, можно сказать, что p0 максимальна в том и только том случае, если:
В дополнение ко всему вышесказанному, в оптимальной гиперссылочной структуре исключаются ссылки, ведущие на страницы, выходящие за переделы линкофарма, поскольку γ = 1 и α + β = 1.
Манипулятивная структура, представленная на Рисунке, 1 удовлетворяет свойствам перечисленным в Теореме 2. Аналогичные структуры также будут удовлетворять свойствам при условии соблюдения собственного подмножества ссылок между целевой и стимулирующими страницами. Экстремальный случай, который заключается в том, что целевой документ цитирует одну стимулирующую страницу, продемонстрирован на Рисунке 3.
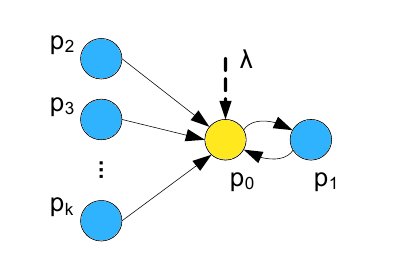
Рисунок 3. Иная оптимальная ссылочная структура единичной спам-фермы с одной целевой страницей
Мы увидели, что в случае использования оптимальной гиперссылочной структуры, целевая страница аккумулирует PageRank из стимулирующих документов, а также по гиперссылкам, проставленным с использованием практики хиджакинга. В этом подразделе мы продемонстрируем, что лекаж может рассматриваться в качестве дополнительного числа стимулирующих страниц. Следовательно, у нас нет необходимости отдельно рассматривать лекаж в оставшейся части текущей работы.
Теорема 3. Для оптимальной спам-фермы, лекаж λ увеличивает целевую оценку аналогично дополнительному числу dλ стимулирующих страниц, где d является константой, зависящей от структуры спам-фермы.
Доказательство. Оценкой PageRank целевой страницей является:
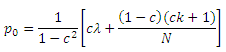
Рассмотрим иную структуру спам-фермы без лекажа, но с наличием дополнительного числа m стимулирующих страниц. Целевой оценкой является:
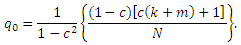
Две оценки равны тогда и только тогда, когда:
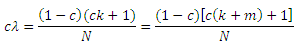
и, таким образом,
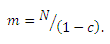
Просим обратить ваше внимание на то, что на практике мы не ожидаем отсутствия лекажа, поскольку это бы говорило о полной изоляции ссылочных ферм от остальной части веба. Лекаж рассматривается нами в качестве дополнительных стимулирующих страниц в целях упрощения изложения настоящего материала, а также наших математических выкладок. Наши результаты могут быть достаточно легко обобщены для случая, при котором наличествует лекаж.
Манипулятивная структура, представленная на Рисунке 1, обладает всеми необходимыми свойствами, посредством которых агент накопления данных системы информационного поиска сможет достичь целевой страницы посредством прохождения хотя бы по одной ссылки, которая была проставлена с использованием технологии хиджакинга, и, таким образом, обойти всю внутреннюю структуру линкофермы. Следовательно, вся спам-ферма будет отсканирована и проиндексирована поисковой машиной, а стимулирующие страницы действительно внесут свой вклад в оценку целевого документа. Несмотря на то, что прохождение робота по ссылкам, проставленным с применением хиджакинга, является важным аспектом достижимости, существует также прочие способы, позволяющие краулеру узнать об определенных веб-документах. Например, для того, чтобы быть уверенным в том, что агент накопления данных поисковой системы достигнет всех страниц спам-фермы, можно разместить каждую из них на отдельном домене. Поскольку поисковые машины обычно сканируют все доменные имена, хранящиеся в базе данных регистратора, подобным способом могут быть отсканированы и проиндексированы все необходимые нам интернет-страницы. Кроме того, для данных целей можно «пожертвовать» некоторыми хиджак-ссылками, проставив их не на целевую, а на стимулирующие страницы. Соответствующая спам-ферма представлена на Рисунке 4 (пунктирными линиями обозначены ссылки, проставленные с использованием техники хиджакинга). Эти альтернативные подходы, касающиеся достижимости станут играть важную роль в наших последующих обсуждениях, когда мы удалим гиперссылки, ведущие с целевого документа на стимулирующие страницы.
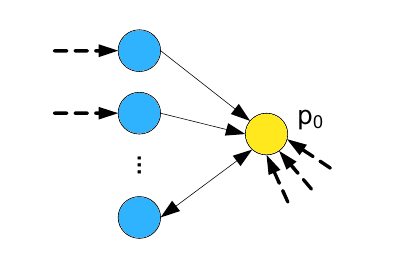
Рисунок 4. Создание стимулирующих страниц, доступных посредством прохождения по гиперссылкам, проставленных с использованием практики хиджакинга.
Первая часть текущей работы рассматривала мошеннические схемы, в которых была задействована единственная спам-ферма. Во второй ее части мы обратим наши взоры на группы спамеров, каждый из которых уже обзавелся своей собственной спам-фермой, и исследуем то, как комплексирование их ферм повлияет на оценки PageRank, присваиваемые целевым страницам. Как упоминалось нами ранее в Разделе 1, подобные типы коллаборационизма появляются в вебе либо потому, что они являются взаимовыгодными для всех участников данного партнерства, либо как результат определенного рода финансового соглашения между «клиентом» и «поставщиком услуг». Для начала в текущем разделе мы выведем формулы, которые количественно оценят характеристики различных манипулятивных альянсов. Затем, в Разделе 5 мы используем выведенные на данном этапе формулы для изучения ряда сценариев манипулятивного сотрудничества.
Давайте для начала обсудим способы, с помощью которых мы можем объединить две оптимальные фермы. Каждая спам-фермы имеют единственную целевую страницу, а также k и m (k<m) стимулирующих веб-страниц соответственно (Как упоминалось нами ранее, лекаж рассматривается как часть стимулирующих документов). Пусть p—0 и q—0 обозначают (максимальные) оценки PageRank целевых документов в том варианте, когда спам-фермы не комплексированы:
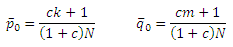
Тогда, p0 и q0 будут обозначать оценки целевых страниц в том варианте, при котором обе спам-фермы комплексированы тем или иным способом. Далее мы исследуем три метода комплексирования.
Существует несколько способов, с помощью которых мы можем объединить две спам-фермы. Один из них заключается в простом цитировании всеми стимулирующими страницами обоих целевых документов так, как это представлено на Рисунке 5.
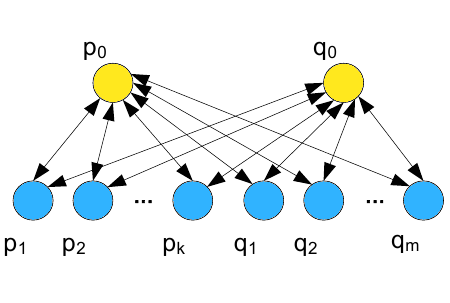
Рисунок 5. Даны две спам-фермы, все стимулирующие документы которых ссылаются на две целевые страницы.
Для того чтобы воссоздать подобную ссылочную структуру, оба спамера добавляют гиперссылки на принадлежащие каждому из них стимулирующие странички, которые теперь ссылаются на целевой документ другого. Следовательно, должно быть добавлено в общем (k+m) новых гиперссылок. Посредством связывания структуры мы получаем две целевые страницы с одинаковыми оценками:
Теорема 4. Для структуры, представленной на Рисунке 5, p0=q0=(p—0 + q—0)/2
Доказательство. Уравнения PageRank для двух комплексированных спам-ферм следующие:
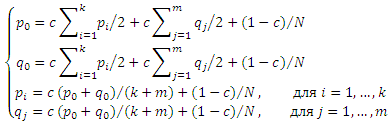
Тогда, p0=q0 и pi=qj. Заменяя pi и qj в первом уравнении, получаем:
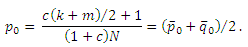
Соответственно, разделение стимулирующих страниц представляет очевидную выгоду для спамера с более меньшей по своим размерам исходной спам-фермой, поскольку PageRank его целевого документа увеличивается с p0 ∝ k до p—0 ∝ (k + m)/2 > k. С другой стороны, разделение не оказывается столь же выгодным для того спамера, который имеет большую по своим размерам исходную ферму, поскольку PageRank его целевого документа уменьшается. Результирующее влияние, достигаемое при разделении стимулирующих страниц, эквивалентно тому сценарию, при котором существуют две не связанные между собой спам-фермы, а (m-k)/2 стимулирующих страниц просто «сдвигаются» от большей по своим размерам фермы к меньшей.
Вместо того чтобы связывать все стимулирующие веб-документы с обеими целевыми страницами, мы можем связать только пару целевых страниц таким образом, что они будут взаимно цитировать друг друга. В этом случае, стимулирующие страницы каждой из двух спам-ферм будут ссылаться только на соответствующие им целевые документы. Кроме того, целевые страницы будут иметь обратные гиперссылки на свои собственные стимулирующие документы. Упрощенный анализ, аналогичный тому, что был выполнен для Теоремы 4, показывает, что эффект, который достигается в случае подобного комплексирования гиперссылочной структуры ничем не отличается от того варианта, при котором все стимулирующие страницы разделялись между спам-фермами: обе целевые страницы получают аналогичную оценку (p—0 + q—0)/2. Просим обратить ваше внимание на то, что на текущем этапе всего чего нам удалось добиться, так это перераспределения, а не увеличения оценок PageRank целевых страниц. Эта структура имеет только одной преимущество по сравнению с той схемой, что была приведена нами в подразделе 4.1.1: количество комплексирующих гиперссылок, которые нам необходимо добавить в модель, уменьшается с (k+m) до 2.
Мы можем сформировать третью возможную манипулятивную структуру, посредством связывания двух целевых страниц и удаления всех обратных ссылок, ведущих на стимулирующие веб-документы так, как это представлено на Рисунке 6.
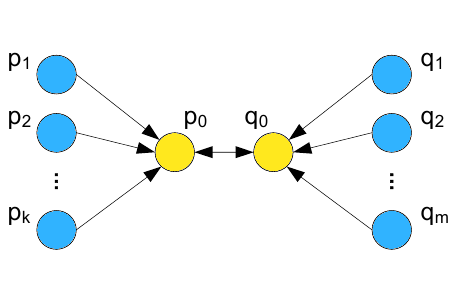
Рисунок 6. Две спам-фермы с взаимосвязанными целевыми страницами
Соответствующие уравнения PageRank получают целевую оценку p0 (q0 симметрична)
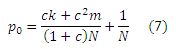
Следующая теорема утверждает, что оценки обоих целевых страниц увеличиваются по сравнению с максимальными значениями, достигаемыми в случае использования несвязанных спам-ферм.
Теорема 5. Для структуры, представленной на Рисунке 6, (p0 – p—0) ∝ m и (q0 – q—0) ∝ k.
Доказательство. Система уравнений, назначающая оценки PageRank интернет-страницам имеет следующую форму:
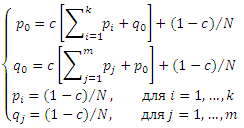
Подставляя pi = qj = (1 − c)/N в первые два уравнения и решая систему, получаем:
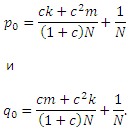
Принимая во внимание оценки p—0 и q—0, можно констатировать, что p0 = p—0 + µm + ν и q0 = q—0 + µk + ν, где
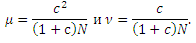
Отсюда рождается вполне естественный вопрос: каким образом оказалось возможным данное улучшение? Поверхностный неформальный анализ поможет нам пролить свет на истину. Давайте сперва взглянем на общий PageRank трех рассмотренных альянсов, те есть на сумму оценок PageRank всех целевых и стимулирующий страниц в каждой манипулятивной структуре. оказывается, что общая оценка совершенно аналогична во всех трех случаях, будучи равной (k+m+2)/N. Также выясняется, что в общем случае всегда наличествует верхняя граница для общей оценки PageRank гиперссылочной структуры с фиксированным набором своих элементов, связанных с остальной частью веба [1]. Теперь давайте сфокусируемся на индивидуальных оценках PageRank стимулирующих страниц. Для третьей манипулятивной структуры, PageRank каждой стимулирующей страницы минимален. В отличие от этого случая, в первых двух гиперссылочных структурах стимулирующие документы имеют более высокую оценку, по причине того, что целевые страницы имеют на них обратные ссылки со своего содержимого. Исключив обратное цитирование в третьей манипулятивной структуре, мы избежали распределения драгоценной доли общей голосующей способности по стимулирующим страницам, которые в любом случае являются иррелевантными. Мы пришли к выводу, что именно третья структура позволяет достичь наиболее высоких целевых оценок по причине более грамотной «организации системы». Общий PageRank ограничен — это гарантирует то, что стимулирующие страницы остаются с низкой голосующей способностью, в то время как все остальные оценки распределяются надлежащим образом среди целевых документов. В действительности, можно продемонстрировать, что данная структура является оптимальной для альянса, состоящего из двух ферм, в том смысле, что она максимизирует сумму оценок PageRank целевых страниц.
Теперь, когда мы с вами знаем, каким образом можно соединить две спам-фермы, имеется смысл продолжить наше обсуждение, касательно манипулятивных альянсов, следуя по логике от малых схем к более крупным формированиям. Мы будем называть подграф целевых страниц ядром альянса. В экстремальном случае, ядром единичной спам-фермы является сама целевая страница. Среди всего изобилия возможных ядерных структур крупных альянсов (вкратце описанных нами в подразделе 4.4) в текущей работе мы сфокусируемся на двух:
Мы последовательно исследуем каждую из этих двух манипулятивных структур. И первым способом связывания целевых документов, за рассмотрение которого мы возьмемся, станет формирование кольца, то есть цикла, который включает в себя все целевые интернет-страницы. Рисунок 7 демонстрирует нам данную структуру для трех спам-ферм.
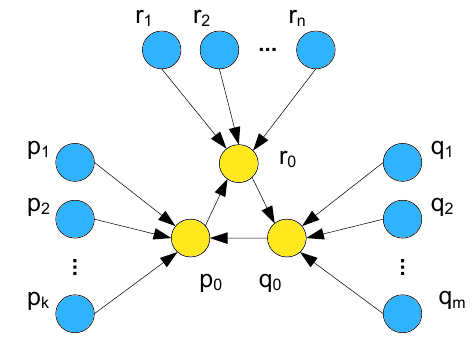
Рисунок 7. Три спам-фермы, которые имеют целевые страницы, формирующие кольцо.

Рисунок 7. Три спам-фермы, которые имеют целевые страницы, формирующие кольцо.
Решение соответствующего матричного уравнения дает следующую оценку PageRank для первой целевой страницы спам-фермы:
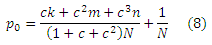
Для более общего случая комплексирования F спам-ферм, посредством формирования кольца целевых документов, давайте обозначим оценку каждой целевой страницы через ti, а число стимулирующих страниц в каждой спам-ферме через bi, где i=1,…,F. Для данной кольцеобразной структуры оценка первой целевой страницы будет рассчитываться как:
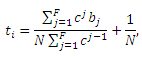
и, более обобщенно, оценкой PageRank целевой страницы i будет:
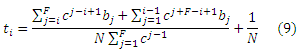
Кроме веб-колец, соединяющих каждую спам-ферму со всеми прочими формациями существует также иной способ перемещения к более крупной гиперссылочной структуре из двух сотрудничающих спам-ферм. Рисунок 8 демонстрирует нам тот случай, при котором сотрудничество спам-ферм организовывается посредством создания полностью связанного подграфа целевых страниц. (Просим обратить ваше внимание на то, что, как и в примере с веб-кольцами, взаимное цитирование целевых документов стимулирующих страниц исключено. На Рисунке 8 стимулирующие страницы опущены.)
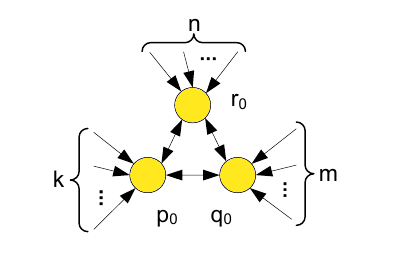
Рисунок 8. Три спам-фермы, которые имеют целевые страницы, формирующие взаимно-связанное ядро.
Решение соответствующего матричного уравнения дает следующую оценку PageRank для первой целевой страницы спам-фермы:
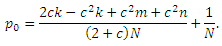
И снова, оценка PageRank каждой целевой страницы оказывается большим, нежели чем тот максимум, что достигается в случае несвязанных между собой ссылочных ферм. Дополнительная оценка поступает от каждого другого целевого документа и их вклад пропорционален количеству стимулирующих страниц, в спам-ферме цели. В общем случае, мы могли бы иметь F ферм с bi стимулирующих страниц для каждой из них, и с оценкой целевой страницы ti, где i=1,…,F. Оценки PageRank целевых документов рассчитываются как:
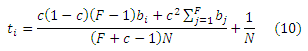
Мы проанализировали два возможных способа связывания целевых интернет-страниц манипулятивного альянса. На текущем этапе нашей работы и в последующих ее разделах мы продолжим фокусироваться на представленной паре структур, однако вместе с тем необходимо подчеркнуть то, что также существуют и другие способы построения ядра альянса. С нашей точки зрения также важно подчеркнуть, что анализ указанных прочих ядерных структур аналогичен тому, который был проведен относительно веб-колец и альянсов со взаимно-связанными ядрами. В этом подразделе мы пробежимся по целому семейству возможных ядер.
Давайте рассмотрим F целевых страниц спам-ферм, состоящих в мошенническом альянсе. Существует 2(F−1)F возможных способов связать узлы F и сформировать ориентированный граф без петель, то есть ребер, инцидентных одному и тому же узлу. Однако далеко не все из возможных графов могут выступить в качестве ядра манипулятивного альянса. В частности, фермы признаются действительно родственными только в том случае, если ядро слабо связанно (weakly connected), то есть сформировавшие его документы связаны основным неориентированным графом. Кроме того, ядро является оптимальным (сумма оценок PageRank целевых страниц достигает своего максимального значения) только в том случае, если оно сильно связанно (strongly connected), то есть существует ориентированный путь от каждой целевой страницы ко всякой другой. В подразделах 4.2 и 4.3 мы исследовали пару структурных альянсов с оптимальными ядрами. Но сколько оптимальных ядер существует для конкретных F? Какие оценки PageRank получат целевые документы каждой спам-фермы? Ответ на первый вопрос оказывается нетривиальным. Действительно, количество сильно-связанных ориентированных графов F = 3, 4, 5,… с количеством узлов = 18, 1606, 565080,… является целочисленной последовательностью Слоуна A003030 [8], для которой в настоящее время нам не известен какого-либо простой аналитический генератор функции. Для того же, чтобы ответить на второй вопрос, отметим следующее: для каждого оптимального ядра возможно получить уравнения, которые дадут нам голосующую способность целевых страниц, точно также как мы поступали при рассмотрении веб-кольца и альянса со взаимно-связанным ядром. В дальнейшем мы постараемся дать количественную интуитивную оценку возможных результатов с использованием наглядных примеров. Рассмотрим альянс, сформированный из F=4 спам-ферм, каждая из которых имеет по 100 стимулирующих страниц. Как упоминалось чуть выше, существует 1606 различных оптимальных ядер, состоящих из 4 сильно-связанных целевых страниц. В простом эксперименте мы рассчитали голосующую способность целевых документов (с параметром c=0.85) для всех ядер. В зависимости от фактической структуры, PageRank каждой целевой страницы может иметь одно из 206 различных значений, варьирующихся в диапазоне от 32.14/N до 165.07/N. Значения покрывают диапазон достаточно равномерно. Следовательно, можно заключит, что возможно получение приблизительно любого распределения оценок PageRank по всем целевым документам, посредством подбора соответствующей ядерной структуры. Обсуждение, касающееся выбора такого ядра, которое отвечает конкретному распределению является темой будущих исследований.
В предыдущих разделах, мы вывели ряд формул, которые помогут нам определить голосующую способность, получаемую целевой страницей в случае применения различных гиперссылочных структур, используемых в спам-фермах. В текущем разделе мы применим наши формулы на практике, демонстрируя то, как полученные нами результаты смогут помочь нам в отчете на ряд практических вопросов, приобретающих в рамках настоящей работы особую важность. Среди всего прочего, мы попытаемся найти ответы на такие вопросы, как: почему одна целевая страница, участвующая в манипулятивном альянсе получает большую оценку, нежели чем другая? Имеет ли смысл новой спам-ферме присоединяться к уже существующему альянсу? Имеет ли смысл линкоферме покинуть тот мошеннический альянс, в котором она участвует? Каким образом подключение дополнительного числа стимулирующих страниц к спам-ферме окажет влияние на ее положение в рамках заданного альянса?
Давайте сперва взглянем на то, что же именно происходит с некоторыми спам-фермами как только они сформируют манипулятивный альянс. Для того, чтобы это наглядно проиллюстрировать, рассмотрим 10 спам-ферм с целевыми страницами t1,…,t10. Первая ферма имеет b1=1000 стимулирующих страниц, вторая имеет b2=2000 стимулирующих страниц и так далее; последняя спам-ферма имеет, соответственно, b10=10000 стимулирующих веб-документов. Мы рассмотрим три сценария. В первом сценарии каждая из указанных спам-ферм могла бы остаться несвязанной с прочими мошенническими схемами, максимизируя голосующую способность своих целевых документов посредством использования той гиперссылочной структуры, которая была представлена на Рисунке 1. Во втором сценарии фермы могли бы сформировать альянс, при котором целевые документы были бы соединены в кольцо: t1 ссылалась бы на t10, t10 ссылалась бы на t9 и так далее до завершения цикла на странице t2, которая бы цитировала документ t1. В третьем сценарии спам-фермы могли быть комплексированы таким образом, что целевые страницы сформировали бы взаимно-связанное ядро. Теперь давайте взглянем на PageRank каждой целевой страницы во всех трех сценариях. Рисунок 9 представляет полученные ими оценки.
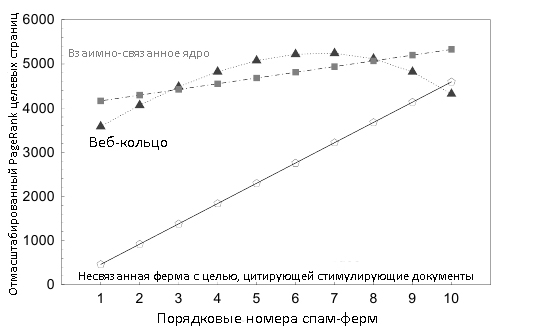
Рисунок 9. Отмасштабированные оценки PageRank целевых страниц спам-ферм, соединенных различными способами.
На оси абсцисс отмечены 10 спам-ферм. Ось ординат соответствует отмасштабированным оценкам PageRank целевых страниц. (Мы отмасштабировали оценки PageRank путем умножения их на N, общее количество веб-страниц. Таким образом, полученные нами отмасштабированные оценки не зависят от размера веба.) Три кривые соответствуют трем нашим сценариям. Как вы можете видеть, для несвязанных спам-ферм голосующая способность целевых веб-документов пропорциональна размеру гиперссылочной фермы. Для того случая, при котором целевые страницы формируют взаимно-связанное ядро, голосующая способность каждого целевого документа увеличивается относительно того сценария, при котором фермы остаются несвязанными. Более того, увеличение оказывается таким, что малые спам-фермы получают большее дополнительных «голосов», а большие — меньше. Еще более интригующим оказывается то, что в случае объединения ферм техникой веб-кольца, оценки некоторые целевых страниц увеличиваются, в то время как прочие веб-документы получают еще меньше «голосов», чем в случае того сценария, при котором фермы остаются несвязанными. В частности, целевые документы крупных спам-ферм, объединенные в кольцо, теряют свою голосующую способность.
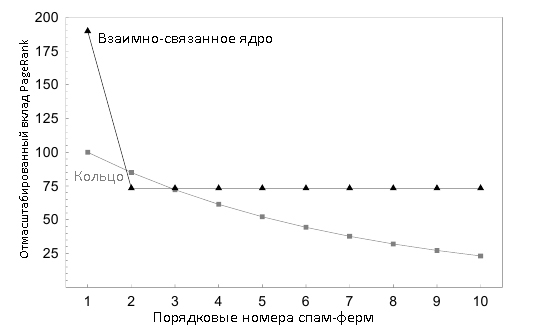
Рисунок 10. Отмасштабированный вклад первой спам-фермы в голосующую способность целевых страниц прочих манипулятивных структур.
Рисунок 10 помогает понять нам наблюдаемые феномены. На нем продемонстрирован вклад первой фермы в оценки PageRank, присуждаемые различным целевым страницам, которые либо объедены техникой кольца, либо с использованием взаимно-связанного ядра. На оси абсцисс снова отмечены 10 спам-ферм. Для каждой фермы i на оси ординат представлена доля отмасштабированного PageRank страницы ti, которая находится с первой фермой в манипулятивном альянсе. Интуитивно, Рисунок 10 демонстрирует преимущество, получаемое каждой структурой от нахождения в альянсе с первой спам-фермой. Просим обратить ваше внимание на то, что в случае взаимно-связанного ядра большая доля PageRank остается за целевым документом первой спам-фермы, а прочие целевые страницы получают существенно меньший по своему размеру, идентичный вклад. Для сравнения, при использовании практики веб-кольца вклад первой спам фермы в себя, а также в прочие формирования менее выражен и уменьшается по мере увеличения расстояния от первой фермы. Давайте выведем формулы, которые следуют из Рисунка 10. Просим обратить ваше внимание на то, что Уравнения 9 и 10 могут быть легко разложены на независимые члены, соответствующие каждой ссылочной ферме, задействованной в альянсе. Соответственно, в случае использования практики веб-кольца вкладом голосующей способности cr(i,i) спам-фермы i в свою собственную целевую страницу i является:
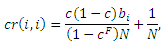
в тоже время вкладом cr(i,j) спам-фермы i в целевую страницу j, i ≠j является:
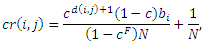
где d(i,j) означают расстояние (или количество шагов) по кольцу между целевыми страницами i и j. Например, с учетом имеющихся 10 спам-ферм, расстояние между целевой страницей t3 и t1 составит 2, в то время как расстояние между t1 и t3 составит 8. Аналогично, само-вклад cc(i,i) для взаимно-связанного ядра рассчитывается как:
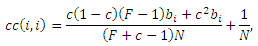
а вклад cc(i,j) спам-фермы i в целевую страницу j, i ≠j:
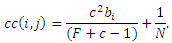
Действительно, если в случае использования практики веб-кольца вклад к прочим целевым документам зависит от дистанции, то при реализации схемы взаимно-связанного ядра оно оказывается равномерным. Также, легко заметить, что общий вклад спам-фермы аналогичен для обоих манипулятивных структур:
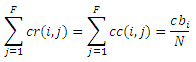
Просим обратить ваше внимание на то, что общий вклад спам-фермы пропорционален количеству стимулирующих страниц. Вклад независим от комплексирования ссылочной структуры между целевыми страницами, при условии, что они не являются стоковыми страницами и только цитируют прочие цели.
С учетом взаимодействия вкладов, по нашему мнению, у нас может появиться новый ряд вопросов. Допустим, давайте рассмотрим существующий альянс и нового спамера, который желал бы в него вступить. При отсутствии какой-либо платы за вход, существующие члены альянса могли бы позволить новичку присоединиться к ним в том случае, если бы после его вступления голосующая способность существующих целевых страниц увеличилась. Мы хотели бы прийти к пониманию того, при каких условиях новая ферма удовлетворяла бы данному критерию.
Для начала давайте ответим на предыдущий вопрос в том сценарии, при котором используются кольцеобразные структуры. Например, рассмотрим вариант добавления новой спам-фермы (линкофарм 3, с оценкой PageRank целевой страницы r0) в кольцо, до этого момента состоящего из альянса двух спам-ферм (линкофармы 1 и 2, с оценками PageRank целевой страницы p0 и q0 соответственно). Используя Уравнения 7 и 8, мы можем рассчитать, что владелец 1 линкофарма увеличивает собственную оценку за счет разрешения спам-ферме 3 присоединиться к существующему альянсу двух только в том случае, если
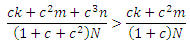
следовательно,
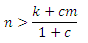
Таким образом, размеры линкофармов 1 и 2 определяют минимальный размер спам-фермы 3, превышение которого становится выгодным для всех участников манипулятивной схемы и делает участие нового линкофарма оправданным с точки зрения общей выгоды. Например, если k=20 и m=10, существующие члены альянса смогли бы позволить организовать с новым линкофармом кольцеобразную структуру только в том случае, если последний имел бы по крайней мере n=16>15.4 стимулирующих страниц. В общем случае, новую спам-ферму выгодно включить в конец веб-кольца, состоящего из F-ферм (то есть, между tF и t1) тогда, когда выполняется следующее неравенство:
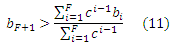
Как вы можете видеть, нижней границей размера линкофарма является средневзвешенное размеров спам-ферм уже задействованных в альянсе. Более того, веса зависят от вставки новой спам-фермы. Интересно отследить то, как точка вставки влияет на минимальный размер ссылочных ферм. Например, рассмотрим Рисунок 11, который демонстрирует нам минимальный размер нового линкофарма в зависимости от точки вставки.
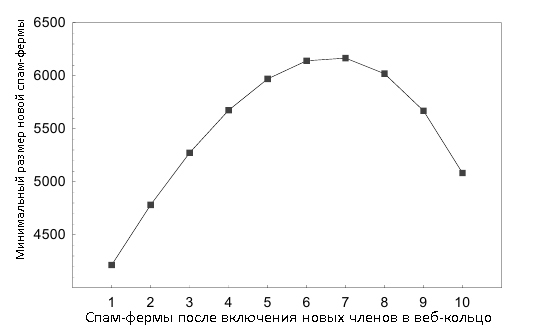
Рисунок 11. Минимальный размер спам-фермы как функция точки вставки на веб-кольце.
На оси абсцисс отмечены спам-фермы, формирующие кольцеобразную структуру до того момента, как мы включим в нее нового члена. К примеру, в том случае, если после включения новой спам-фермы их количество составит 3, тогда новая ферма должна быть вставлена между 2 и 3 линкофармом, указывая на t2. На оси ординат отмечен минимальный размер, отвечающий условиям Уравнения 11. К примеру, если новая ссылочная ферма включается перед линкофармом 1, тогда ее минимальный размер составляет только 4216; в том же случае, если новая ферма вставляется перед линкофармом 7, тогда ее минимальный размер составляет 6167.
Давайте также исследуем вопрос, относительно того, при каких факторах оказывается выгодным включение нового участника в альянс, имеющий взаимно-связанное ядро. К сожалению, в том сценарии, когда целевые страницы являются полностью связанными, ответ на него более затруднителен, нежели чем в случае с кольцеобразными гиперссылочными структурами. Здесь, новый участник с bF+1 стимулирующих страниц включается в манипулятивную схему (то есть посредством его включения увеличивается оценка каждой из существующих до него целевых документов) только в том случае, если он удовлетворяет следующим неравенствам для i=1,…,F:
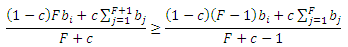
Упрощая выражения, мы получаем неравенство для каждого bi:
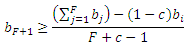
К счастью, более
детальное рассмотрение неравенств показывает достаточность удовлетворения одного из них, чтобы также удовлетворить все прочие:
Теорема 6. Только неравенства, соответствующие наименьшей спам-ферме, которая уже присутствует в манипулятивном альянсе, определяют минимальный размер нового линкофарма.
Доказательство. Пусть b* представляет собой количество стимулирующих страниц в наименьшей по своим размерам спам-ферме так, что b* ≥ bi, i=1,…,F. Легко заметить, что для всякой ссылочной фермы i,
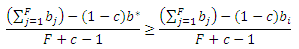
Соответственно, если bF+1 удовлетворяет
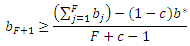
также удовлетворяются все остальные неравенства.
Следовательно, нижняя граница, относительно количества стимулирующих страниц нового участника задается следующим неравенством:
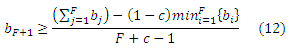
Отсюда, мы можем найти удовлетворяющую нас приблизительную нижнюю границу размера новой спам-фермы. Введем η ≥ 1, такое, что ηb* соответствует среднеарифметической размера ссылочных ферм, состоящих в альянсе. Следовательно, предыдущее неравенство можно переписать в следующем виде:
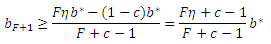
Поскольку F >> (c-1), у нас имеются все основания предположить, что
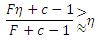
Следовательно, если новая спам-ферма удовлетворяет Уравнению 12, она также удовлетворяет bF+1 ≥ ηb*, а текущий усредненный размер спам-фермы ηb* крайне близок к нижней границе (но ниже) минимального размера нового линкофарма. Для того, чтобы проиллюстрировать полученные нами выше результаты, давайте рассмотрим альянс двух комплексированных спам-ферм с k=20 и m=10 стимулирующих страниц. Имеет смысл принять третью ферму и, таким образом, сформировать альянс со взаимно-связанным ядром, если
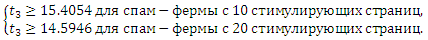
Следовательно, третья ссылочная ферма должна иметь по крайней мере 16 стимулирующих страниц.
Мы также можем задать себе следующий вопрос: при каких обстоятельствах ссылочной ферме, которая уже состоит в манипулятивном альянсе, имеет смысл отколоться от него и продолжить свое существование в качестве автономной единицы? Мы видели на Рисунке 9, что целевая страница t10 имеет наименьшее значение PageRank в кольцеобразной структуре, чем это было бы в том случае, если бы она существовала независимо от прочих ферм. Наша интуиция заключается в том, что вклад ссылочной фермы 10 в другие формации слишком велик, но сама она не может получить достаточный объем компенсирующих голосов от прочих линкофармов. Давайте формализуем данную интуицию посредством получения соответствующих неравенств для кольцеобразной структуры и альянсов со взаимно-связанным ядрами.
Гиперссылочной ферме следует выйти из манипулятивного альянса в том случае, если PageRank ее целевого документа оказывается ниже, чем в том варианте, когда спам-ферма существовала бы независимо от остальных формаций, и имела бы ту оптимальную внутреннюю ссылочную структуру, что была продемонстрирована нами на Рисунке 1. Соответствующим неравенством для первой спам-фермы, состоящей в веб-кольце, является:
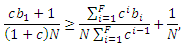
заканчивая решение
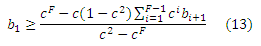
Например, ферма 1 должна располагать 11389 стимулирующих страниц для того, чтобы у ее владельца появился смысл выйти из кольцеобразной структуры. С другой стороны, предел для нахождения 10-ой ссылочной указанной схеме составляет 9091 страниц. Поскольку данный размер составляет 10000, что превышает указанный лимит, голосующая способность спам-фермы 10 оказывается ниже, чем если бы она существовала независимо от прочих линкофармов.
Аналогичным образом, у спам-фермы 1 появляется резон покинуть альянс со взаимно-связанным ядром в том случае, если выполняются следующее неравенство:
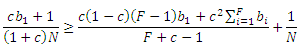
Решением является:
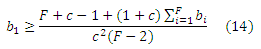
Здесь различия между минимальными размерами различных спам-ферм оказываются меньшими, чем в случае реализации кольцеобразных структур; вклад каждой из них распределяется более равномерно. Например, пределом для нахождения фермы 1 в альянсе является 14693, в то время как для фермы 10 он составляет 12445. Поскольку ни одна из данных ссылочных ферм не достигает предельного размера (см. Рисунок 9), каждой из них логично продолжить свое существование в рамках текущего манипулятивного альянса.
Другая ситуация, которая может возникнуть заключается желании спамера, участвующего в манипулятивном альянсе, добавить большее число стимулирующих страниц в принадлежащую ему спам-ферму. Данное увеличение количества стимулирующих страниц увеличивает вклад ссылочной фермы в собственную целевую страницу, а также ко всем прочим участникам альянса, следуя модели, продемонстрированной на Рисунке 10. Очевидно, что добавление большего числа новых стимулирующих страниц приближает спам-ферму к тому предельному состоянию, при котором у ее владельца появляется резон отколоться от альянса, как это указано в Неравенствах 13 и 14. Вопрос заключается в следующем: для фермы i, имеющей заданный размер, сколько необходимо добавить стимулирующих страниц чтобы ей было выгоднее работать отдельно от остальных? Мы можем найти ответ на указанный вопрос, если взглянем на разницу между минимальным размером, определенным Неравенствами 13 и 14, и текущим размером спам-фермы. На Рисунке 12 представлены соответствующие результаты для наших 10 гиперссылочных ферм, соединенных либо с использованием кольцеобразной структуры, либо с применением альянса со взаимно-связанным ядром.
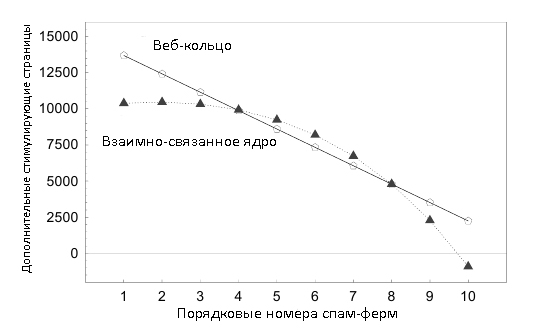
Рисунок 12. Дополнительное число стимулирующих страниц, необходимых для выхода спам-фермы из альянса.
На оси абсцисс отмечены 10 спам-ферм; ось ординат представляет собой минимальное число дополнительных стимулирующих страниц, добавляемых спамером для того, чтобы PageRank целевой страницы его собственной спам-фермы оказался выше после его выхода из манипулятивного альянса, нежели чем тот PageRank, который она имеет, продолжая свое существование в этой мошеннической схеме. Например, если ферма 3 с текущим количеством стимулирующих страниц в 3000 получит порядка 10000 дополнительных веб-документов, она сможет достичь более высокой голосующей способности целевой страницы в том случае, если отделиться от альянса со взаимно-связанным ядром, нежели чем останется в нем и дальше. Просим учесть, что ферма 10 уже достигла своего предела для нахождения в кольцеобразной структуре. В данном случае, спамер может пожелать покинуть альянс, отказавшись от некоторых стимулирующих страниц или возложив на других «потерю», понесенную им в связи со своим пребыванием в манипулятивном альянсе.
До этого момента наш анализ фокусировался на оптимальных структурах линкофармов, а также на том, как они могут комплексироваться. Однако в случае применения известных нам оптимальных структур, мы можем вычислять ссылочные фермы без особого труда (см. Раздел 7), поэтому спамеры могут попытаться отойти от лучших структур в целях обеспечения собственной безопасности, даже в том случае, если ранжирование принадлежащих им целевых документов ухудшится. Тем не менее, для того, чтобы не потерять слишком много «голосов», мошенники не пожелают отходить от данных оптимальных структур полностью, лишь немного модифицируя их. Это означает, что «реальные» структуры будут по-прежнему напоминать те, которые были изучены нами в ходе текущей работы. В качестве наглядной иллюстрации, давайте рассмотрим граф, изображенный на Рисунке 13.
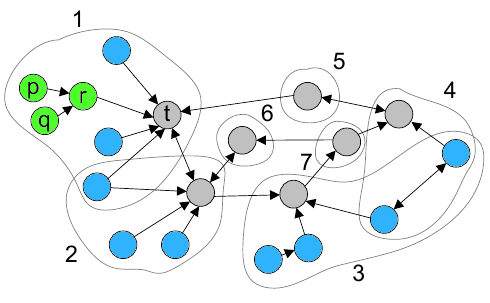
Рисунок 13. Манипулятивный альянс с иррегулярной структурой.
То, что на первый взгляд может показаться иррегулярной, запутанной структурой, в действительности является мошенническим альянсом, состоящим из семи спам-ферм, и который может быть проанализирован в качестве такового. Например, на Рисунке 13 мы можем идентифицировать ряд определенных стимулирующих структур. Группа страниц {p,q,r} является подобного рода структурой, которая оказывает саппортизацию целевой странице t. Стимулирующие структуры всегда могут быть смоделированы посредством эквивалентного числа обычных стимулирующих документов, только с одной ссылкой на целевую страницу. Например, глядя на Рисунок 13 видно, что вклад группы {p,q,r} эквивалентен 2×0.85+1=2.7 обычным стимулирующим страницам. Общая стимуляция целевого документа t становится равной тому, что производится числом b1 = 5.2 обычных стимулирующих страниц. После подсчета всех стимулирующих страниц, мы обнаруживаем, что общий стимулирующий эффект, затрагивающий весь манипулятивный альянс, эквивалентен тому, что b = 11.55 простым стимулирующим страницам. Мы также обнаружили, что целевые страницы (узлы серого цвета) формируют оптимальное ядро. Соответственно, общий целевой PageRank составляет (cb + 7)/N.
Таки образом, встречающиеся на практике ссылочные структуры могут быть смоделированы эквивалентированием оптимальных структур. В частности, эффект сложных стимулирующих структур может быть достаточно просто смоделирован посредством эквивалентного количества обычных стимулирующих страниц так, как это было проиллюстрировано в предыдущем примере. Лекаж также может быть включен в нашу модель так, как если бы он являлся некоторым числом дополнительных стимулирующих документов, что упоминалось нами в подразделе 3.4. Те ссылочные структуры, которые комплексируют целевые страницы, могут быть реализованы как по типу кольца, так и по типу взаимно-связанного ядра, или в виде одного из графов, рассмотренных нами в подразделе 4.4. В заключении, мы полагаем, что та ценная аналитическая информация, которая была получена нами в контексте регулярных спам-ферм и альянсов также будет справедлива для обобщенных структур ссылочного спама.
В настоящей работе мы изучили спам-фермы и альянсы с точки зрения своего создателя — спамера: какие структуры являются оптимальными? Каким образом они могут быть комплексированы? В чем состоят затраты и получаемая выгода в том случае, если спамеры объединяются в альянс? Мы уже упоминали, что принятие стороны мошенников может предоставить полезнейшую инсайдерскую информацию для противодействия тем инструментам, с помощью которых они оказывают давление на ранжирующие механизмы результатов органического поиска. В конце концов, как можно бороться с поисковым спамом не зная о том, что он из себя представляет? Конечно, понимание ферм и альянсов не влечет за собою автоматическое решение проблемы обнаружения манипулятивных схем. На самом деле, технология обнаружения находится только в зачаточном состоянии, и пока разработчики поиска создают эффективные инструменты, нацеленные на противодействие спаму, спамеры адаптируют и реализуют более устойчивые схемы. В этом завершающем нашу работу разделе мы вкратце пройдемся по некоторым технологиям детекции поискового спама, которые были разработаны на сегодняшний день, и мы утверждаем, что принятие научным сообществом стороны тех, кто занимается продвижением сайтов, оказало немаловажную роль в разработке данных технологий. Основная идея обнаружения спама заключается в прямой или опосредованной идентификации манипулятивных структур, наподобие тех, что были изучены нами в рамках настоящей работы. Несмотря на то, что наличие в вебе подобного рода гиперссылочных структур не обязательно свидетельствует о реализации запрещенных технологий ссылочного спама, данный факт может указывать на потенциальную возможность его наличия. Далее мы обозначим в общих чертах две схемы, которые применяются разработчикам поиска в задачах нейтрализации некоторых форм ссылочного спама.
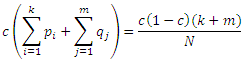
Соотношение между двумя
суммами имеет порядок

То есть, целевые страницы усиливают вклад стимулирующих страниц на коэффициент равный примерно 1/(1-c). Данный эффект достигается за счет сильной взаимосвязанности между целевыми документами, и его можно также наблюдать в других оптимальных альянсах, которые были представлены нами ранее. На основании предыдущего наблюдения, Zhang и др [9] предложили методологию идентификации сильно взаимосвязанных групп интернет-страниц. Для всякой группы страниц H они определили коэффициент усиления (amplification factor) Amp(H), который представляет собой всего лишь отношение между общим PageRank страниц в группе и вклада, возвращаемого от прочих интернет-документов, находящихся за пределами указанной группы, как это было проиллюстрировано нами в Уравнении 15. В том случае, если коэффициент усиления группы близок к 1/(1-c), то это говорит нам о том, что веб-страницы исследуемой группы состоят в тайном сговоре. Поскольку целевые страницы манипулятивных альянсов также участвуют в тайном сговоре, мы можем выявить их по соответствующим коэффициентам усиления.
Технологии, которые мы представили вам в самых общих чертах, безусловно, являются полезными в выявлении спама, однако они все еще далеки от совершенства. Решение 1 зачастую не способно идентифицировать иррегулярные структуры ссылочных ферм (наподобие той, что была продемонстрирована на Рисунке 13), которые характерны для более софистических (и высоко-ранжируемых) спамерских схем. Решение 2 идентифицирует любую группу страниц, которая, тем не менее, может и не быть мошеннической. (Например, в тайном сговоре страниц могут быть уличены блоги, которые просто имеют частое взаимное цитирование). таким образом, по сути это не является технологией обнаружения поискового спама, хотя и может играть ключевую роль по части его обнаружения. Представленные решения идентифицируют только некоторые документы, состоящие в спам-ферме или манипулятивном альянсе и, как правило, относящиеся к ядру. Другие технологии, такие как спектральный анализ матрицы со-цитирования, могут использоваться в качестве инструмента для выявления прочих связанных спам-страниц.
Предоставленный нами анализ демонстрирует то, каким образом может быть максимизирован PageRank целевых страниц, состоящих в спам-фермах. наиболее важное в текущей работе было то, что мы обнаружили существование целого класса манипулятивных структур, использование которых позволяет достичь наибольшей оценки PageRank целевого документа. Все данные оптимальные структуры спам-ферм имеют следующие общие характеристики:
Мы исследовали то, каким образом спамеры, изначально имеющие автономные спам-фермы, могут кооперироваться и создавать манипулятивные альянсы, которые увеличивают оценки целевых страниц, присваиваемые алгоритмом PageRank. Мы представили оптимальные альянсы двух гиперссылочных ферм, а также познакомили вас с двумя возможными структурами, используемых в крупных альянсах; одна из которых объединяет целевые документы в веб-кольцо, а другая формирует из них взаимно-связанное ядро. Наш основной вывод заключается в том, что альянсы могут увеличить голосующую способность каждой целевой страницы, состоящей в альянсе; распределение оценок целевых страниц, присваиваемых алгоритмом PageRank, зависит того способа комплексирования данных целевых документов. Мы также проанализировали динамику альянсов, определяя, при каких условиях новой спам-ферме имеет смысл войти в манипулятивный альянс или, наоборот, покинуть его, в том случае если она уже является его членом. Как утверждалось, первый, критически важный шаг в противодействии поисковому спаму заключается в понимании того, против чего мы ведем борьбу. Мы полагаем, что наш анализ гиперссылочных ферм и манипулятивных альянсов обеспечит твердое понимание некоторых спамерских техник, а также приведет к выработке эффективных схем противодействия ссылочному спаму.
Перевод материала «Link Spam Alliances» выполнил Константин Скоморохов
Полезная информация по продвижению сайтов:
Перейти ко всей информации